2022-2023学年黑龙江省哈尔滨市七下数学期末达标测试试题含答案

2022-2023学年黑龙江省哈尔滨市七下数学期末达标测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生须知：

1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题(每小题3分,共30分)

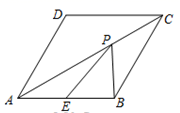
1．如图，在菱形中，=120°，点E是边的中点，P是对角线上的一个动点，若AB=2，则PB+PE的最小值是（    ）

A．1 B． C．2 D．

2．方程x（x＋1）＝x＋1的解是（      ）

A．x1=0，x2=－1    B．x = 1    C．x1 = x2 = 1    D．x1 = 1，x2=－1

3．点关于轴对称的点的坐标是（  ）

A． B． C． D．

4．做抛掷两枚硬币的实验，事件“一正一反”的“频率”的值正确的是（    ）

A．0 B．约为 C．约为 D．约为1

5．在平面直角坐标系中，点O为原点，直线y=kx+b交x轴于点A（﹣2，0），交y轴于点B．若△AOB的面积为8，则k的值为（　　）

A．1 B．2 C．﹣2或4 D．4或﹣4

6．关于一个四边形是不是正方形，有如下条件①对角线互相垂直且相等的平行四边形；②对角线互相垂直的矩形；③对角线相等的菱形；④对角线互相垂直平分且相等的四边形；以上条件，能判定正方形的是(    )

A．①②③ B．②③④ C．①③④ D．①②③④

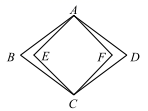
7．如图，在菱形ABCD中，E，F分别是AB，AC的中点，若∠B=50°，则∠AFE的度数为（　　）

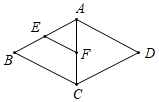
A．50° B．60° C．65° D．70°

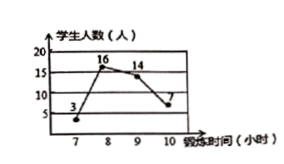
8．如图所示是根据某班级名同学一周的体育锻炼情况绘制的统计图，由图像可知该班同学一周参加体育锻炼时间的中位数，众数分别是（   ）

A．，

B．，

C．，

D．，

9．下列因式分解正确的是（    ）

A．x2+2x-1=(x-1)2    B．a2-a=a(a+1)

C．m2+(-n)2=(m+n)(m-n)    D．-9+4y2=(3+2y)(2y-3)

10．生物学家发现：生物具有遗传多样性，遗传密码大多储存在分子上.一个分子的直径约为0.0000002，这个数用科学计数法可以表示为（    ）

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．若一个多边形的每一个内角都是144°，则这个多边形的是边数为_____.

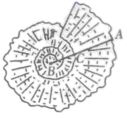
12．如图是一种贝壳的俯视图，点C分线段AB近似于黄金分割（AC>BC）．已知AB=10cm，则AC的长约为__________cm．（结果精确到0.1cm）

13．如图，已知菱形的面积为24，正方形的面积为18，则菱形的边长是__________．

14．将点A（1，-3）向左平移3个单位长度，再向上平移5个单位长度后得到的点A′的坐标为 ______________．

15．列不等式：据中央气象台报道，某日我市最高气温是33℃，最低气温是25℃，则当天的气温t(℃)的变化范围是______．

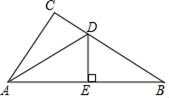
16．如图，在△ABC中，∠B＝32°，∠BAC的平分线AD交BC于点D，若DE垂直平分AB，则∠C的度数为_____．

三、解下列各题(本大题共8小题，共72分)

17．（8分）在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为个单位长度，按要求作图：

①画出关于原点的中心对称图形；

②画出将绕点逆时针旋转得到

③请在网格内过点画一条直线将平分成两个面积相等的部分．

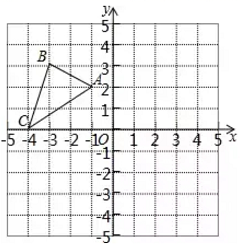
18．（8分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）.

(1) 请画出△ABC向左平移5个单位长度后得到的△ABC；

(2) 请画出△ABC关于原点对称的△ABC；

(3) 在轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标.

19．（8分）定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径。

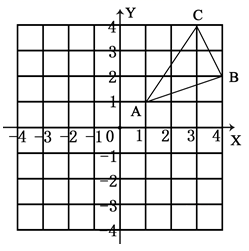
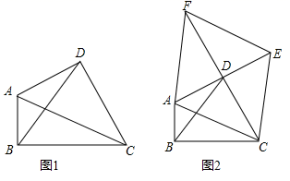
（1）如图1，损矩形ABCD，∠ABC＝∠ADC＝90°，则该损矩形的直径是线段AC，同时我们还发现损矩形中有公共边的两个三角形角的特点，在公共边的同侧的两个角是相等的。如图1中：△ABC和△ABD有公共边AB，在AB同侧有∠ADB和∠ACB，此时∠ADB＝∠ACB；再比如△ABC和△BCD有公共边BC，在CB同侧有∠BAC和∠BDC，此时∠BAC＝∠BDC。请再找一对这样的角来         ＝       

（2）如图2，△ABC中，∠ABC＝90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连结BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由。

（3）在第（2）题的条件下，若此时AB＝，BD＝，求BC的长。

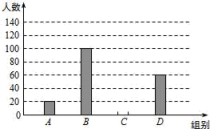
20．（8分）国家规定“中小学生每天在校体育活动时间不低于1h”，为此，某市就“每天在校体育活动”时间的问题随机调查了辖区内320名初中学生，根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：

A组：t＜0.5h；B组：0.5h≤t＜1h；C组：1h≤t＜1.5h；D组：t≥1.5h

请根据上述信息解答下列问题：

（1）C组的人数是　  ；

（2）本次调查数据的中位数落在　   组内；

（3）若该市辖区内约有32000名初中学生，请你估计其中达国家规定体育活动时间的人约有多少？

21．（8分）已知是不等式的一个负整数解，请求出代数式的值．

22．（10分）已知一次函数的图象经过点（-2，-7）和（2，5），求该一次函数解析式并求出函数图象与y轴的交点坐标.

23．（10分）某学习小组在学习了函数及函数图象的知识后，想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.

（1）列函数表达式：若矩形的周长为8，设矩形的一边长为x，面积为y，则有y=____________；

（2）上述函数表达式中，自变量x的取值范围是____________；

（3）列表：

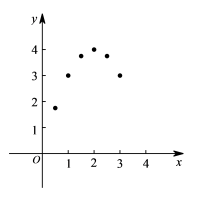
写出m=____________；

（4）画图：在平面直角坐标系中已描出了上表中部分各对应值为坐标的点，请你画出该函数的图象；

（5）结合图象可得，x=____________时，矩形的面积最大；写出该函数的其它性质（一条即可）：____________.

24．（12分）某水果专卖店销售樱桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每千克降低1元，则平均每天的销售可增加10千克，请回答：

（1）写出售价为50元时，每天能卖樱桃_____千克，每天获得利润_____元．

（2）若该专卖店销售这种樱桃要想平均每天获利2240元，每千克樱桃应降价多少元？

（3）若该专卖店销售这种樱桃要想平均每天获利最大，每千克樱桃应售价多少元？

参考答案

一、选择题(每小题3分,共30分)

1、B

2、D

3、A

4、C

5、D

6、D

7、C

8、B

9、D

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、6.2

13、1

14、 (-2，2)

15、25≤t≤1．

16、84°．

三、解下列各题(本大题共8小题，共72分)

17、（1）作图见解析    （2）作图见解析    （3）作图见解析

18、（1）图形见解析；

（2）图形见解析；

（3）图形见解析，点P的坐标为：（2，0）

19、（1）∠ABD=∠ACD；（2）四边形ACEF为正方形，理由见解析；（3）5.

20、（1）根C组的人数为140人；（2）调查数据的中位数落在C组；（3）达国家规定体育活动时间的人约有20000人．

21、，原式

22、y=3x-1, 函数图象与y轴的交点坐标(0,-1).

23、见解析

24、200    2000（2）4元或6元（3）当销售单价为55元时，可获得销售利润最大