2022-2023学年黑龙江省哈尔滨市风华中学七年级数学第二学期期末教学质量检测试题含答案

2022-2023学年黑龙江省哈尔滨市风华中学七年级数学第二学期期末教学质量检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

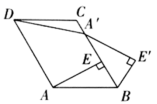
1．如图，在平行四边形中，于点E，以点B为中心，取旋转角等于，将顺时针旋转，得到．连接，若，，则的度数为（    ）

A． B． C． D．

2．已知关于x的方程mx2+2x﹣1＝0有实数根，则m的取值范围是（　　）

A．m≥﹣1 B．m≤1 C．m≥﹣1且m≠0 D．m≤1且m≠0

3．若分式有意义，则的值是（    ）

A． B． C． D．

4．已知 x＝－1 是一元二次方程 x2＋px＋q＝0 的一个根，则代数式 p－q 的值是（    ）

A．1 B．－1 C．2 D．－2

5．如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是（　　）

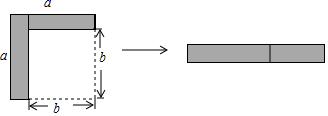
A．（a﹣b）2＝a2﹣2ab+b2 B．a（a﹣b）＝a2﹣ab

C．（a﹣b）2＝a2﹣b2 D．a2﹣b2＝（a+b）（a﹣b）

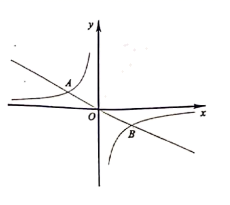
6．下列各曲线表示的与的关系中，不是的函数的是（   ）

A． B．

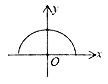C． D．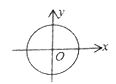

7．某人从一鱼摊上买了三条鱼，平均每条元，又从另一个鱼摊上买了两条鱼，平均每条元，后来他又以每条元的价格把鱼全部卖给了乙，结果发现赔了钱，原因是

A． B． C． D．与大小无关

8．已知三角形的三边为2、3、4，该三角形的面积为(    )

A． B． C． D．

9．为迎接“义务教育均衡发展”检查，我市抽查了某校七年级8个班的班额人数，抽查数据统计如下：52,49,56,54,52,51,55,54，这四组数据的众数是（ ）

A．52和54    B．52

C．53    D．54

10．在平行四边形ABCD中，∠A+∠C=160°，则∠B的度数是（　　）

A．130° B．120° C．100° D．90°

二、填空题(本大题共有6小题，每小题3分，共18分)

11．若直角三角形的两边长分别为1和2，则斜边上的中线长为_____.

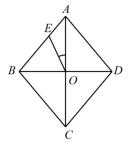
12．如图，已知菱形ABCD的一个内角∠BAD=80°，对角线AC，BD相交于点O，点E在AB上，且BE=BO，则∠EOA=___________°.

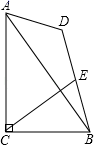
13．如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，点D为平面内动点，且满足AD＝4，连接BD，取BD的中点E，连接CE，则CE的最大值为_____．

14．定义运算“★”：对于任意实数 ，都有 ，如：．若，则实数 的值是_____．

15．在比例尺1∶8000000的地图上，量得太原到北京的距离为6.4厘米，则太原到北京的实际距离为公里。

16．四边形ABCD中，AD∥BC，AD=BC，对角线AC、BD相交于点O，若CD＝3cm，△BOC的周长比△AOB的周长大2cm，则四边形ABCD的周长＝______cm．

三、解下列各题(本大题共8小题，共72分)

17．（8分）已知，直线与双曲线交于点，点.

（1）求反比例函数的表达式；

（2）根据图象直接写出不等式的解集            .

（3）将直线沿轴向下平移后，分别与轴，轴交于点，点，当四边形为平行四边形时，求直线的表达式.

18．（8分）如图，四边形是正方形，是边所在直线上的点，，且交正方形外角的平分线于点.

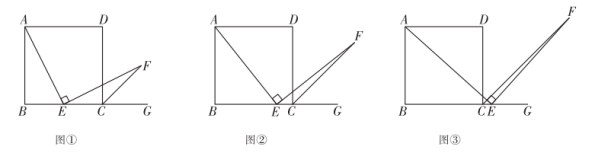
（1）当点在线段中点时（如图①），易证，不需证明；

（2）当点在线段上（如图②）或在线段延长线上（如图③）时，（1）中的结论是否仍然成立？请写出你的猜想，并选择图②或图③的一种结论给予证明.

19．（8分）某公司把一批货物运往外地，有两种运输方案可供选择．

方案一：使用快递公司的邮车运输，装卸收费400元，另外每千米再回收4元；

方案二：使用快递公司的火车运输，装卸收费820元，另外每千米再回收2元．

（1）分别求邮车、火车运输总费用y1（元）、y2（元）关于运输路程x（km）之间的函数关系式：

（2）如何选择运输方案，运输总费用比较节省？

20．（8分）化简分式（）÷ ，并在 2，3，4，5 这四个数中取一个合适的数作为 a 的值代入求值．

21．（8分）先化简，再求值：÷（2+），其中x=﹣1．

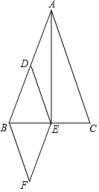
22．（10分）如图，在中，，是中线，点是的中点，连接，且，

（1）求证：四边形是菱形；

（2）若，直接写出四边形的面积．

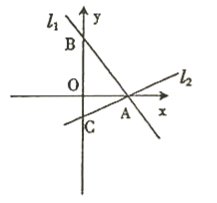
23．（10分）如图，已知直线与交轴于点，，分别交轴于点，，，的表达式分别为，.

（1）求的周长；

（2）求时，的取值范围.

24．（12分）如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF，

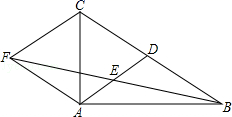
（1）求证：AF=DC；

（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

参考答案

一、选择题(每小题3分,共30分)

1、D

2、A

3、D

4、A

5、D

6、D

7、A

8、D

9、A

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1或

12、1

13、1．

14、3或﹣1．

15、512

16、16

三、解下列各题(本大题共8小题，共72分)

17、（1）；（2）或；（3）,

18、（1）见解析；（2）成立，理由见解析.

19、（1）y1=4x+400，y2=2x+820；（2）当运输路程x不超过210千米时，使用方式一最节省费用；当运输路程x超过210千米时，使用方式二最节省费用；当运输路程x等于210千米时，使用两种方式的费用相同．

20、，取代入，原式．  

21、当x=﹣1时，原式==．

22、（1）见解析；（2）.

23、（1）的周长；（2）

24、（1）见解析（2）见解析