


2022-2023学年重庆市渝中区名校数学七年级第二学期期末质量检测试题含答案
展开这是一份2022-2023学年重庆市渝中区名校数学七年级第二学期期末质量检测试题含答案,共7页。试卷主要包含了若分式有意义,则的取值范围是,一次函数的图象大致是等内容,欢迎下载使用。
2022-2023学年重庆市渝中区名校数学七年级第二学期期末质量检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.若正比例函数y=kx的图象经过点(1,2),则k的值为
A.![]() B.-2 C.
B.-2 C.![]() D.2
D.2
2.下列各式中,属于分式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.实数a,b在数轴上的位置如图所示,则化简代数式|a+b|−a的结果是( )

A.2a+b B.2a C.a D.b
4.《九章算术》是中国古代的数学专著,是“算经十书”(汉唐之间出现的十部古算书)中最重要的一种.书中有下列问題:“今有邑方不知大小,各中开门,出北门八十步有木,出西门二百四十五步见木,问邑方有几何?”意思是:如图,点![]() 、点
、点![]() 分别是正方形
分别是正方形![]() 的边
的边![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 过点
过点![]() ,
,![]() 步,
步,![]() 步,则正方形的边长为( )
步,则正方形的边长为( )
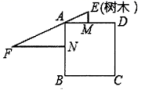
A.![]() 步 B.
步 B.![]() 步 C.
步 C.![]() 步 D.
步 D.![]() 步
步
5.2013年,某市发生了严重干旱,该市政府号召居民节约用水,为了解居民用水情况,在某小区随机抽查了10户家庭的月用水量,结果统计如图,则关于这10户家庭的月用水量,下列说法错误的是( )
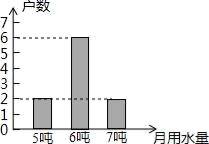
A.众数是6 B.极差是2 C.平均数是6 D.方差是4
6.若分式![]() 有意义,则
有意义,则![]() 的取值范围是( )
的取值范围是( )
A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]() .
.
7.在二次根式![]() 中,a能取到的最小值为( )
中,a能取到的最小值为( )
A.0 B.1 C.2 D.2.5
8.一次函数![]() 的图象大致是( )
的图象大致是( )
A. B.
B.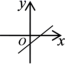 C.
C.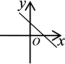 D.
D.
9.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
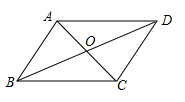
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
10.一次函数 y 2x 2 的大致图象是( )
A.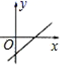 B.
B.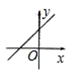 C.
C.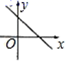 D.
D.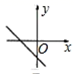
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知一组数据3,5,9,10,x,12的众数是9,则这组数据的平均数是___________.
12.为了解宿迁市中小学生对春节联欢晚会语言类节目喜爱的程度,这项调查采用__________方式调查较好(填“普查”或“抽样调查”).
13.若分式![]() 有意义,则实数x的取值范围是_______.
有意义,则实数x的取值范围是_______.
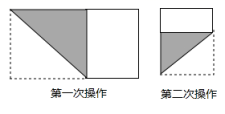
14.把长为20,宽为a的长方形纸片(10<a<20),如图那样折一下,剪下一个边长等于长方形宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的长方形为正方形,则操作停止.当n=3时,a的值为________.
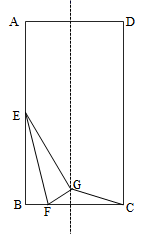
15.如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上的一动点,将
边上的一动点,将![]() 沿
沿![]() 折叠,使得点
折叠,使得点![]() 落在
落在![]() 处,连接
处,连接![]() ,
,![]() ,当点
,当点![]() 落在矩形
落在矩形![]() 的对称轴上,则
的对称轴上,则![]() 的值为______.
的值为______.
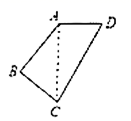
16.如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,则
,则![]() ______度.
______度.
三、解下列各题(本大题共8小题,共72分)
17.(8分)阅读材料,解答问题:
有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:![]() 的有理化因式是
的有理化因式是![]() ;1﹣
;1﹣![]() 的有理化因式是1+
的有理化因式是1+![]() .
.
分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.如:
![]() ﹣1,
﹣1,![]() .
.
请根据上述材料,计算:![]() 的值.
的值.
18.(8分)如图,等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 是斜边
是斜边![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 翻折得
翻折得![]() ,连接
,连接![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的长是______.
的长是______.
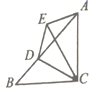
19.(8分)已知:如图,在▱ABCD中,点E、F分别在BC、AD上,且BE=DF
求证:AC、EF互相平分.
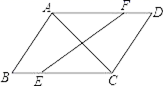
20.(8分)如图1,在平面直角坐标系中,矩形OABC如图所示放置,点A在x轴上,点B的坐标为(n,1)(n>0),将此矩形绕O点逆时针旋转90°得到矩形OA′B′C′,抛物线y=ax2+bx+c(a≠0)经过A、A′、C′三点.
(1)求此抛物线的解析式(a、b、c可用含n的式子表示);
(2)若抛物线对称轴是x=1的一条直线,直线y=kx+2(k≠0)与抛物线相交于两点D(x1,y1)、E(x2、y2)(x1<x2),当|x1﹣x2|最小时,求抛物线与直线的交点D和E的坐标;
(3)若抛物线对称轴是x=1的一条直线,如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接MQ′、PQ′,当△PMQ′与平行四边形APQM重合部分的面积是平行四边形的面积的![]() 时,求平行四边形APQM的面积.
时,求平行四边形APQM的面积.
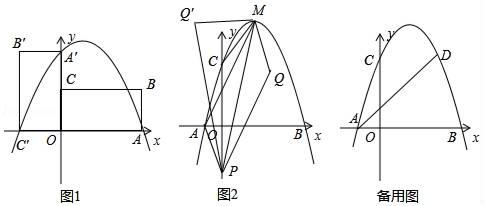
21.(8分)如图,在长方形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 以2厘米/秒的速度向终点
以2厘米/秒的速度向终点![]() 移动,点
移动,点![]() 以1厘米/秒的速度向
以1厘米/秒的速度向![]() 移动,当有一点到达终点时,另一点也停止运动.设运动的时间为
移动,当有一点到达终点时,另一点也停止运动.设运动的时间为![]() ,问:
,问:
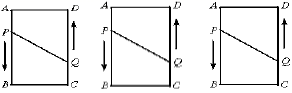
(1)当![]() 秒时,四边形
秒时,四边形![]() 面积是多少?
面积是多少?
(2)当![]() 为何值时,点
为何值时,点![]() 和点
和点![]() 距离是
距离是![]() ?
?
(3)当![]() _________时,以点
_________时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.(直接写出答案)
为顶点的三角形是等腰三角形.(直接写出答案)
22.(10分)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接 CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为6,∠ABC=60°,求AE的长.
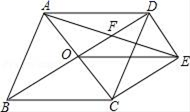
23.(10分)如图是一块地的平面图,AD=4m,CD=3m,AB=13m,BC=12m,∠ADC=90°,求这块地的面积.
24.(12分)已知一次函数的图象经过![]() ,
,![]() 两点.
两点.
(1)求这个一次函数的解析式;
(2)试判断点![]() 是否在这个一次函数的图象上;
是否在这个一次函数的图象上;
(3)求此函数图象与![]() 轴,
轴,![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、D
4、A
5、D
6、B
7、C
8、A
9、A
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1.
12、抽样调查
13、![]()
14、12或2
15、2
16、1
三、解下列各题(本大题共8小题,共72分)
17、![]()
18、![]() 或
或![]()
19、证明见解析
20、(3)y=﹣x2+(n﹣3)x+n;(2)D(﹣3,5),E(3,4);(2)5或3.
21、(1)5厘米2;(2)![]() 秒或
秒或![]() 秒;(3)
秒;(3)![]() 秒或
秒或![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
22、(1)见解析;(2)![]()
23、24m2
24、(1)![]() ;(2)
;(2)![]() 不在这个一次函数的图象上;(3)函数图象与
不在这个一次函数的图象上;(3)函数图象与![]() 轴,
轴,![]() 轴围成的三角形的面积=4.
轴围成的三角形的面积=4.
相关试卷
这是一份重庆市渝中区名校2023-2024学年数学九上期末质量检测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
这是一份重庆市渝中区名校2023-2024学年数学八上期末综合测试模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列各式不能分解因式的是,若分式有意义,则的取值范围为,若分式的值为零,则x的值是,如图,已知,则,估计的值等内容,欢迎下载使用。
这是一份2023-2024学年重庆市渝中区名校数学八年级第一学期期末学业质量监测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,在、、、、中分式的个数有.等内容,欢迎下载使用。












