

2022-2023学年贵州省黔南州瓮安四中学数学七年级第二学期期末教学质量检测模拟试题含答案
展开2022-2023学年贵州省黔南州瓮安四中学数学七年级第二学期期末教学质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.下图是外周边缘为正八边形的木花窗挂件,则这个八边形的每个内角为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图,在平行四边形ABCD中,下列结论一定正确的是( ).
A.AB=AD B.OA=OC C.AC=BD D.∠BAD=∠ABC
3.如图,将▱ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )
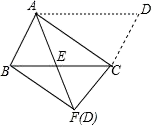
A.1 B.2 C.3 D.4
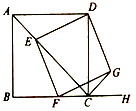
4.下列式子中,可以表示为![]() 的是( )
的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知直角三角形的两条边长分别是3和5,那么这个三角形的第三条边的长( )
A.4 B.16 C.![]() D.4或
D.4或![]()
6.若![]() =﹣a
=﹣a![]() ,则a的取值范围是( )
,则a的取值范围是( )
A.﹣3≤a≤0 B.a≤0 C.a<0 D.a≥﹣3
7.关于二次函数y=﹣2x2+1,以下说法正确的是( )
A.开口方向向上 B.顶点坐标是(﹣2,1)
C.当x<0时,y随x的增大而增大 D.当x=0时,y有最大值﹣![]()
8.如图,点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在双曲线
在双曲线![]() ,
,![]() 轴,分别过点
轴,分别过点![]() 、
、![]() 向
向![]() 轴作垂线,垂足分别为
轴作垂线,垂足分别为![]() 、
、![]() .若矩形
.若矩形![]() 的面积是
的面积是![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.下列调查适合抽样调查的是( )
A.审核书稿中的错别字
B.对某校八一班同学的身高情况进行调查
C.对某校的卫生死角进行调查
D.对全县中学生目前的睡眠情况进行调查
10.方程![]() 的解是
的解是
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.如图所示,平行四边形![]() 中,点
中,点![]() 在边
在边![]() 上,以
上,以![]() 为折痕,将
为折痕,将![]() 向上翻折,点
向上翻折,点![]() 正好落在
正好落在![]() 上的
上的![]() 处,若
处,若![]() 的周长为8,
的周长为8,![]() 的周长为22,则
的周长为22,则![]() 的长为__________.
的长为__________.
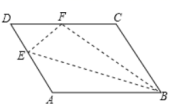
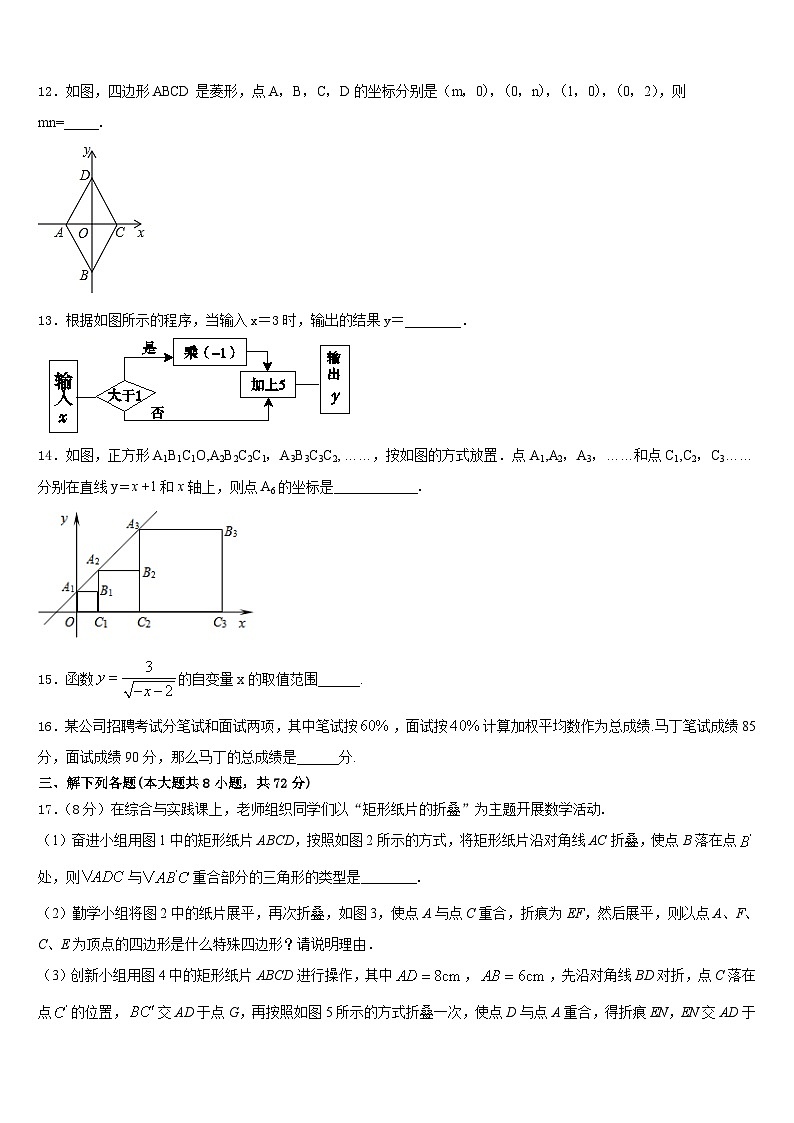
12.如图,四边形ABCD是菱形,点A,B,C,D的坐标分别是(m,0),(0,n),(1,0),(0,2),则mn=_____.
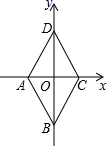
13.根据如图所示的程序,当输入x=3时,输出的结果y=________.
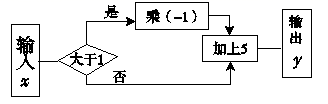
14.如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2, ……,按如图的方式放置.点A1,A2,A3,……和点C1,C2,C3……分别在直线y=x +1和x轴上,则点A6的坐标是____________.
15.函数![]() 的自变量x的取值范围______.
的自变量x的取值范围______.
16.某公司招聘考试分笔试和面试两项,其中笔试按![]() ,面试按
,面试按![]() 计算加权平均数作为总成绩.马丁笔试成绩85分,面试成绩90分,那么马丁的总成绩是______分.
计算加权平均数作为总成绩.马丁笔试成绩85分,面试成绩90分,那么马丁的总成绩是______分.
三、解下列各题(本大题共8小题,共72分)
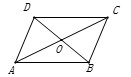
17.(8分)在综合与实践课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.
(1)奋进小组用图1中的矩形纸片ABCD,按照如图2所示的方式,将矩形纸片沿对角线AC折叠,使点B落在点![]() 处,则
处,则![]() 与
与![]() 重合部分的三角形的类型是________.
重合部分的三角形的类型是________.
(2)勤学小组将图2中的纸片展平,再次折叠,如图3,使点A与点C重合,折痕为EF,然后展平,则以点A、F、C、E为顶点的四边形是什么特殊四边形?请说明理由.
(3)创新小组用图4中的矩形纸片ABCD进行操作,其中![]() ,
,![]() ,先沿对角线BD对折,点C落在点
,先沿对角线BD对折,点C落在点![]() 的位置,
的位置,![]() 交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.
交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.

18.(8分)如图,已知四边形![]() 为正方形,点
为正方形,点![]() 为对角线
为对角线![]() 上的一动点,连接
上的一动点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
(1)求证:矩形![]() 是正方形;
是正方形;
(2)判断![]() 与
与![]() 之间的数量关系,并给出证明.
之间的数量关系,并给出证明.
19.(8分)计算:(![]() )0﹣|
)0﹣|![]() ﹣2|﹣
﹣2|﹣![]() .
.
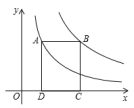
20.(8分)小明一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量q(升)与行驶时间t(小时)之间的关系如图所示.

根据图象回答下列问题:
(1)小汽车行驶 小时后加油,中途加油 升;
(2)求加油前油箱余油量q与行驶时间t的函数关系式;
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速为80km/h,要到,达目的地,油箱中的油是否够用?请说明理由.
21.(8分)已知:直线y=2x+6、直线y=﹣2x﹣4与y轴的交点分别为A点、B点.
(1)请直接写出点A、B的坐标;
(2)若两直线相交于点C,试求△ABC的面积.
22.(10分)某区对即将参加中考的初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
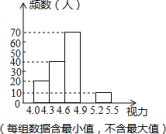
(1)本次调查的样本为 ,样本容量为 ;
(2)在频数分布表中,组距为 ,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,计算抽样中视力正常的百分比.
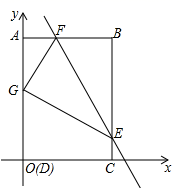
23.(10分)如图,四边形ABCD为矩形,C点在![]() 轴上,A点在
轴上,A点在![]() 轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).
轴上,D(0,0),B(3,4),矩形ABCD沿直线EF折叠,点B落在AD边上的G处,E、F分别在BC、AB边上且F(1,4).
(1)求G点坐标
(2)求直线EF解析式
(3)点N在坐标轴上,直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形?若存在,直接写出M点坐标;若不存在,请说明理由
24.(12分)解不等式组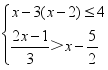
参考答案
一、选择题(每小题3分,共30分)
1、D
2、B
3、C
4、A
5、D
6、A
7、C
8、A
9、D
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1.
12、1 .
13、1
14、(31,32)
15、x<-2
16、1
三、解下列各题(本大题共8小题,共72分)
17、(1)等腰三角形(或钝角三角形);(2)菱形,理由详见解析;(3)![]() .
.
18、(1)详见解析;(2)![]() ,理由详见解析.
,理由详见解析.
19、-1-![]()
20、(1)3;24;(2)Q=﹣10t+36(0≤t≤3);(3)油箱中的油是够用的.
21、(1)点A的坐标为(0,6)、B的坐标(0,﹣4);(2)△ABC的面积为12.1.
22、(1)从中抽取的200名即将参加中考的初中毕业生的视力;200;(2)0.3;60;0.05,见解析;(3)70%.
23、(1)G(0,4-![]() );(2)
);(2)![]() ;(3)
;(3)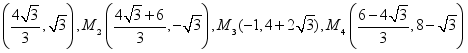 .
.
24、1≤x<6.1
贵州省黔南州瓮安四中学2023-2024学年九年级数学第一学期期末调研模拟试题含答案: 这是一份贵州省黔南州瓮安四中学2023-2024学年九年级数学第一学期期末调研模拟试题含答案,共6页。试卷主要包含了等于等内容,欢迎下载使用。
2023-2024学年贵州省黔南州瓮安县九年级数学第一学期期末教学质量检测模拟试题含答案: 这是一份2023-2024学年贵州省黔南州瓮安县九年级数学第一学期期末教学质量检测模拟试题含答案,共8页。试卷主要包含了方程的解是,把二次函数化成的形式是下列中的,下列方程中,是一元二次方程的是等内容,欢迎下载使用。
2023-2024学年贵州省黔南州瓮安县八年级数学第一学期期末考试模拟试题含答案: 这是一份2023-2024学年贵州省黔南州瓮安县八年级数学第一学期期末考试模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,在,分式的个数有,如图,下列各式中正确的是,点A所在象限为等内容,欢迎下载使用。












