


2022-2023学年赤峰市重点中学七年级数学第二学期期末考试模拟试题含答案
展开2022-2023学年赤峰市重点中学七年级数学第二学期期末考试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.一元二次方程![]() 的一次项系数为( )
的一次项系数为( )
A.1 B.![]() C.2 D.-2
C.2 D.-2
2.如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
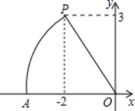
A.﹣4和﹣3之间 B.3和4之间 C.﹣5和﹣4之间 D.4和5之间
3.若二次根式![]() 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A.x>![]() B.x≥
B.x≥![]() C.x≤
C.x≤![]() D.x≤5
D.x≤5
4.我校是教育部的全国青少年校园足球“满天星”训练基地,旨在“踢出快乐,拼出精彩”,如图,校园足球图片正中的黑色正五边形的内角和是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列说法错误的是( )
A.必然事件发生的概率为1 B.不确定事件发生的概率为0.5
C.不可能事件发生的概率为0 D.随机事件发生的概率介于0和1之间
6.如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E,则下列结论正确的是( )
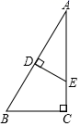
A.AE=3CE B.AE=2CE C.AE=BD D.BC=2CE
7.下列等式成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.下列关于直线![]() 的说法正确的是( )
的说法正确的是( )
A.经过第一、二、四象限 B.与![]() 轴交于点
轴交于点![]()
C.![]() 随
随![]() 的增大而减小 D.与
的增大而减小 D.与![]() 轴交于点
轴交于点![]()
9.用配方法解方程x2﹣![]() x﹣1=0时,应将其变形为( )
x﹣1=0时,应将其变形为( )
A.(x﹣![]() )2=
)2=![]() B.(x+
B.(x+![]() )2=
)2=![]()
C.(x﹣![]() )2=0 D.(x﹣
)2=0 D.(x﹣![]() )2=
)2=![]()
10.不等式组![]() 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A.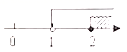 B.
B.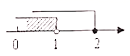
C.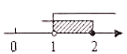 D.
D.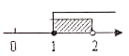
11.若二次函数![]() 的图象经过点P(-2,4),则该图象必经过点( )
的图象经过点P(-2,4),则该图象必经过点( )
A.(2,4) B.(-2,-4) C.(-4,2) D.(4,-2)
12.《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( ).
A. B.
B. C.
C. D.
D.
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.若代数式![]() 的值等于0,则x=_____.
的值等于0,则x=_____.
14.甲、乙、丙三人进行射击测试,每人10次射击成绩的平均值都是8.9环,方差分别是S甲2=0.53,S乙2=0.51,S丙2=0.43,则三人中成绩最稳定的是______(填“甲”或“乙”或“丙”)
15.已知 ![]() ,那么
,那么![]() 的值为____________.
的值为____________.
16.将直线y=2x-3向上平移5个单位可得______直线.
17.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.
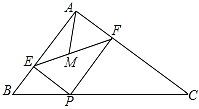
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
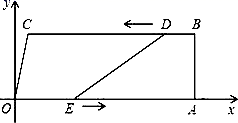
18.(5分)如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
(1)当t为何值时,四边形ABDE是矩形;
(2)当t为何值时,DE=CO?
(3)连接AD,记△ADE的面积为S,求S与t的函数关系式.
19.(5分)已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
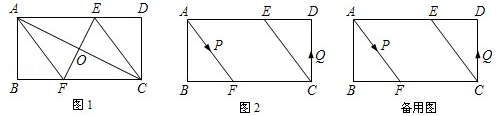
(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.
①问在运动的过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.
②若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
20.(8分)某欢乐谷为回馈广大谷迷,在暑假期间推出学生个人门票优惠价,各票价如下:
票价种类 | (A)学生夜场票 | (B)学生日通票 | (C)节假日通票 |
单价(元) | 80 | 120 | 150 |
某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生,其中购买的B种票数是A种票数的3倍还多7张,C种票y张.
(1)直接写出y与x之间的函数关系式;
(2)设购票总费用为w元,求w(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不低于20张,且每种票至少购买5张,则有几种购票方案?并指出哪种方案费用最少.
21.(10分)(2013年广东梅州8分)为建设环境优美、文明和谐的新农村,某村村委会决定在村道两旁种植A,B两种树木,需要购买这两种树苗1000棵.A,B两种树苗的相关信息如表:
| 单价(元/棵) | 成活率 | 植树费(元/棵) |
A | 20 | 90% | 5 |
B | 30 | 95% | 5 |
设购买A种树苗x棵,绿化村道的总费用为y元,解答下列问题:
(1)写出y(元)与x(棵)之间的函数关系式;
(2)若这批树苗种植后成活了925棵,则绿化村道的总费用需要多少元?
(3)若绿化村道的总费用不超过31000元,则最多可购买B种树苗多少棵?
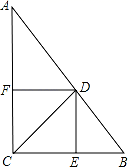
22.(10分)已知:如图Rt△ABC中,∠ACB=90°,CD为∠ACB的平分线,DE⊥BC于点E,DF⊥AC于点F.
求证:四边形CEDF是正方形.
23.(12分)某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是________分,众数是________分;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、A
3、B
4、C
5、B
6、B
7、D
8、D
9、D
10、C
11、A
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、2
14、丙
15、1
16、y=1x+1
17、1.2
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、 (1)t=![]() ;(2)t=6;(3)S=
;(2)t=6;(3)S=![]() t2﹣13t.
t2﹣13t.
19、(1)证明见解析;(2)AF=5cm;(3)①有可能是矩形,P点运动的时间是8,Q的速度是0.5cm/s;②t=![]() .
.
20、(1)y=93-4x;(2)w=-160x+14790;(3) 共有3种购票方案, 当A种票为22张,B种票73张,C种票为5张时费用最少,最少费用为11270元.
21、(1)y=﹣10x+1;(2)30000元;(3)600棵.
22、证明见解析
23、(1)84.5,84;
(2)笔试成绩和面试成绩所占的百分比分别是40%,60%;
(3)综合成绩排序前两名的人选是4号和2号选手.
辽阳市重点中学2022-2023学年数学七年级第二学期期末考试模拟试题含答案: 这是一份辽阳市重点中学2022-2023学年数学七年级第二学期期末考试模拟试题含答案,共6页。试卷主要包含了下列命题是假命题的是等内容,欢迎下载使用。
海南市重点中学2022-2023学年七年级数学第二学期期末考试试题含答案: 这是一份海南市重点中学2022-2023学年七年级数学第二学期期末考试试题含答案,共7页。试卷主要包含了下列说法正确的是,估计的值应在等内容,欢迎下载使用。
山西省重点中学2022-2023学年数学七年级第二学期期末考试模拟试题含答案: 这是一份山西省重点中学2022-2023学年数学七年级第二学期期末考试模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,已知分式的值是零,那么x的值是,若,则=,在平面直角坐标系中,点M等内容,欢迎下载使用。












