


2022-2023学年贵州省六盘水市名校七年级数学第二学期期末联考模拟试题含答案
展开2022-2023学年贵州省六盘水市名校七年级数学第二学期期末联考模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若四边形的两条对角线相等,则顺次连接该四边形各边中点所得的四边形是( )
A.梯形 B.矩形 C.菱形 D.正方形
2.下列条件中,不能判定一个四边形是平行四边形的是( )
A.两组对边分别平行 B.一组对边平行且相等 C.两组对角分别相等 D.一组对边相等且一组对角相等
3.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则劣弧AC的长是( )
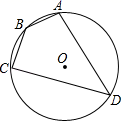
A.4π B.2π C.π D.![]()
4.为了解某小区家庭垃圾袋的使用情况,小亮随机调查了该小区 ![]() 户家庭一周的使用数量,结果如下(单位:个):
户家庭一周的使用数量,结果如下(单位:个):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .关于这组数据,下列结论错误的是( )
.关于这组数据,下列结论错误的是( )
A.极差是 ![]() B.众数是
B.众数是 ![]() C.中位数是
C.中位数是 ![]() D.平均数是
D.平均数是 ![]()
5.如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1,![]() ),则点C的坐标为( )
),则点C的坐标为( )
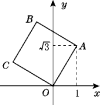
A.(-![]() ,1) B.(-1,
,1) B.(-1,![]() ) C.(
) C.(![]() ,1) D.(-
,1) D.(-![]() ,-1)
,-1)
6.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量![]() (升)与行驶时间
(升)与行驶时间![]() (小时)之间的函数关系的图象是( )
(小时)之间的函数关系的图象是( )
A.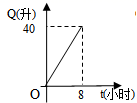 B.
B.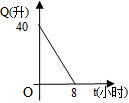
C.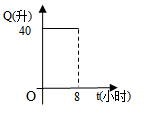 D.
D.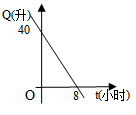
7.要使二次根式![]() 有意义,x必须满足( )
有意义,x必须满足( )
A.x≤2 B.x≥2 C.x<2 D.x>2
8.现有一组数据:3、4、5、5、6、6、6、6、7,若去掉其中一个数6则不受影响的是( )
A.众数 B.中位数 C.平均数 D.众数和中位数
9.如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )
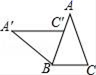
A.40° B.70° C.80° D.140°
10.对于反比例函数![]() ,下列说法中不正确的是( )
,下列说法中不正确的是( )
A.图像经过点(1.-2)
B.图像分布在第二第四象限
C.x>0时,y随x增大而增大
D.若点A(![]() )B(
)B(![]() )在图像上,若
)在图像上,若![]() ,则
,则![]()
11.已知一次函数![]() 与
与![]() 的图象如图,则下列结论:①
的图象如图,则下列结论:①![]() ;②
;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 的解为
的解为![]() ;④当
;④当![]() 时,
时,![]() ,其中正确的个数是
,其中正确的个数是![]()
![]()
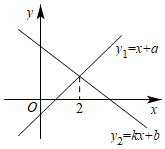
A.1 B.2 C.3 D.4
12.如图,矩形ABCD中,对角线AC=8cm,△AOB是等边三角形,则AD的长为( )cm.
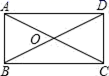
A.4 B.6 C.4![]() D.3
D.3![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
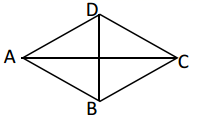
13.如图,菱形![]() 的周长为20,对角线
的周长为20,对角线![]() 的长为6,则对角线
的长为6,则对角线![]() 的长为______.
的长为______.
14.已知5+![]() 的整数部分为a,5-
的整数部分为a,5-![]() 的小数部分为b,则a+b的值为__________
的小数部分为b,则a+b的值为__________
15.2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.
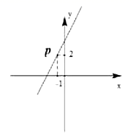
16.如图,直线![]() 经过点
经过点![]() ,则不等式
,则不等式![]() 的解集为________________.
的解集为________________.
17.一次函数![]() 图象经过一、三、四象限,则反比例函数
图象经过一、三、四象限,则反比例函数![]() 的函数值随
的函数值随![]() 的增大而__________.(填增大或减小)
的增大而__________.(填增大或减小)
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2),M,N两点之间的距离,可以用公式MN=![]() 计算.
计算.
解答下列问题:
(1)若已知点A(1,2),B(4,-2),求A,B两点间的距离;
(2)在(1)的条件下,点O是坐标原点,判断△AOB是什么三角形,并说明理由.
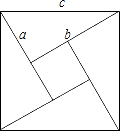
19.(5分)如图1,边长为![]() 的大正方形中有一个边长为
的大正方形中有一个边长为![]() 的小正方形(
的小正方形(![]() ),图2是由图1中阴影部分拼成的一个长方形.
),图2是由图1中阴影部分拼成的一个长方形.
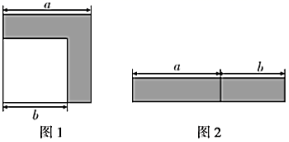
(1)观察图1、图2,当用不同的方法表示图形中阴影部分的面积时,可以获得一个因式分解公式,则这个公式是_______;
(2)如果大正方形的边长![]() 比小正方形的边长
比小正方形的边长![]() 多3,它们的面积相差57,试利用(1)中的公式,求
多3,它们的面积相差57,试利用(1)中的公式,求![]() ,
,![]() 的值.
的值.
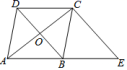
20.(8分)如图,已知菱形![]() 的对角线相交于点
的对角线相交于点![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连结
,连结![]() .
.
![]() 求证:
求证:![]() .
.
![]() 当
当![]() 时,四边形
时,四边形![]() 为菱形吗?请说明理由.
为菱形吗?请说明理由.
21.(10分)如图,已知边长为6的菱形ABCD中,∠ABC=60°,点E,F分别为AB,AD边上的动点,满足![]() ,连接EF交AC于点G,CE、CF分别交BD于点M,N,给出下列结论:①△CEF是等边三角形;②∠DFC=∠EGC; ③若BE=3,则BM=MN=DN;④
,连接EF交AC于点G,CE、CF分别交BD于点M,N,给出下列结论:①△CEF是等边三角形;②∠DFC=∠EGC; ③若BE=3,则BM=MN=DN;④![]() ; ⑤△ECF面积的最小值为
; ⑤△ECF面积的最小值为![]() .其中所有正确结论的序号是______
.其中所有正确结论的序号是______
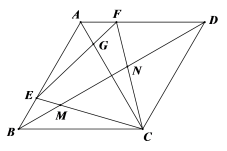
22.(10分)如果一组数据﹣1,0,2,3,x的极差为6
(1)求x的值;
(2)求这组数据的平均数.
23.(12分)解不等式![]() ,并将解集表示在数轴上.
,并将解集表示在数轴上.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、D
3、B
4、B
5、A
6、B
7、B
8、A
9、B
10、D
11、C
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、8
14、12-![]()
15、1
16、![]() .
.
17、增大
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)A,B两点间的距离AB=5;(2)△AOB是直角三角形,见解析.
19、(1)![]() ;(2)a=11,b=1
;(2)a=11,b=1
20、(1)详见解析;(2)详见解析.
21、①②③⑤
22、(1)x=1或x=-3;(2)![]() 或
或![]()
23、![]() ,见解析
,见解析
2023-2024学年贵州省黔南州名校九上数学期末联考模拟试题含答案: 这是一份2023-2024学年贵州省黔南州名校九上数学期末联考模拟试题含答案,共8页。试卷主要包含了如图,中,,在中,=90〫,,则的值是,抛物线的对称轴是等内容,欢迎下载使用。
贵州省六盘水市名校2023-2024学年八上数学期末调研试题含答案: 这是一份贵州省六盘水市名校2023-2024学年八上数学期末调研试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,在下列图形中是轴对称图形的是,已知,为实数且满足,,设,,化简,其结果是,下列实数中,无理数是等内容,欢迎下载使用。
贵州省六盘水市第四实验中学2022-2023学年七年级数学第二学期期末联考模拟试题含答案: 这是一份贵州省六盘水市第四实验中学2022-2023学年七年级数学第二学期期末联考模拟试题含答案,共8页。试卷主要包含了已知一次函数,则该函数的图象是等内容,欢迎下载使用。












