


2022-2023学年福建省宁德市福鼎市数学七下期末学业质量监测模拟试题含答案
展开2022-2023学年福建省宁德市福鼎市数学七下期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.我省某市五月份第二周连续七天的空气质量指数分别为:111、96、47、68、70、77、105,则这七天空气质量指数的平均数是( )
A.71.8 B.77 C.82 D.95.7
2.学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )
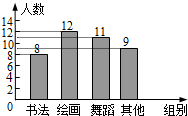
A.0.1 B.0.15
C.0.25 D.0.3
3.如图,在![]() 中,
中,![]() 的平分线与
的平分线与![]() 的垂直平分线交于点
的垂直平分线交于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.把函数![]() 向上平移3个单位,下列在该平移后的直线上的点是( )
向上平移3个单位,下列在该平移后的直线上的点是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若反比例函数的图象经过点(﹣1,2),则它的解析式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m 远,该同学的身高为1.7m ,则树高为( ).
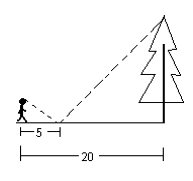
A.3.4m B.4.7 m C.5.1m D.6.8m
7.用公式解方程﹣3x2+5x﹣1=0,正确的是( )
A.x=![]() B.x=
B.x=![]() C.x=
C.x=![]() D.x=
D.x=![]()
8.如图,把一个边长为1的正方形放在数轴E,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数为( ).
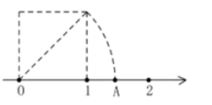
A.2 B.1.4 C.3 D.1.7
9.用反证法证明:“直角三角形至少有一个锐角不小于45°”时,应先假设( )
A.直角三角形的每个锐角都小于45°
B.直角三角形有一个锐角大于45°
C.直角三角形的每个锐角都大于45°
D.直角三角形有一个锐角小于45°
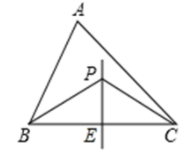
10.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
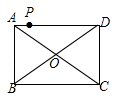
A.4.8 B.5 C.6 D.7.2
二、填空题(本大题共有6小题,每小题3分,共18分)
11.若![]() 有意义,则字母x的取值范围是 .
有意义,则字母x的取值范围是 .
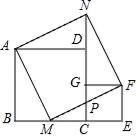
12.如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M是BC边上一个动点,联结AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转恰好至△NGF.给出以下三个结论:①∠AND=∠MPC; ②△ABM≌△NGF;③S四边形AMFN=a1+b1.其中正确的结论是_____(请填写序号).
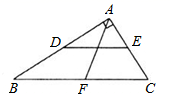
13.如图,在Rt△ABC中,已知∠BAC=90°,点D、E、F分别是三边的中点,若AF=3cm,则DE=_____cm.
14.直线![]() 与直线
与直线![]() 平行,则
平行,则![]() ______.
______.
15.已知:![]() ,
,![]() ,代数式
,代数式![]() 的值为_________.
的值为_________.
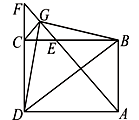
16.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,点G是EF的中点,连接CG、BG、BD、DG,下列结论:① BC=DF,②∠DGF=135o;③BG⊥DG,④ 若3AD=4AB,则4S△BDG=25S△DGF;正确的是____________(只填番号).
三、解下列各题(本大题共8小题,共72分)
17.(8分)某中学需要添置一批教学仪器,方案一:到厂家购买,每件原价40元,恰逢厂家促销活动八折出售;方案二学校自己制作,每件20元,另外需要制作工具的租用费600元;设该学校需要购买仪器x件,方案一与方案二的费用分别为y1和y2(元)
(1)请分别求出y1,y2关于x的函数表达式;
(2)若学校需要购买仪器30~60(含30和60)件,问采用哪种方案更划算?请说明理由.
18.(8分)在四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 的直线分别交边
的直线分别交边![]() 、
、![]() 、
、![]() 、
、![]() 于点
于点![]() 、
、![]() 、
、![]() 、
、![]()
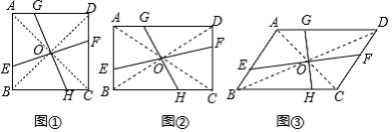
(1)如图①,若四边形![]() 是正方形,且
是正方形,且![]() ,易知
,易知![]() ,又因为
,又因为![]() ,所以
,所以![]() (不要求证明)
(不要求证明)
(2)如图②,若四边形![]() 是矩形,且
是矩形,且![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长(用含
的长(用含![]() 、
、![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)如图③,若四边形![]() 是平行四边形,且
是平行四边形,且![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
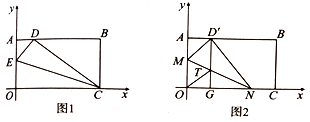
19.(8分)将一矩形纸片![]() 放在直角坐标系中,
放在直角坐标系中,![]() 为原点,点
为原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() .
.
(1)如图1,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上的
边上的![]() 点处,求直线
点处,求直线![]() 的解析式;
的解析式;
(2)如图2,在![]() 边上选取适当的点
边上选取适当的点![]() ,将
,将![]() 沿
沿![]() 折叠,使
折叠,使![]() 点落在
点落在![]() 边上的点
边上的点![]() 处,过
处,过![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于
于![]() 点,连接
点,连接![]() ,判断四边形
,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)、在(2)的条件下,若点![]() 坐标
坐标![]() ,点
,点![]() 在
在![]() 直线上,问坐标轴上是否存在点
直线上,问坐标轴上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,若存在,请直接写出点
为顶点的四边形是平行四边形,若存在,请直接写出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
20.(8分)某一公路的道路维修工程,准备从甲、乙两个工程队选一个队单独完成,根据两队每天的工程费用和每天完成的工程量可知,若由两队合做6天可以完成,共需工程费用385200元;若单独完成,甲队比乙队少用5天,每天的工程费用甲队比乙队多4000元。
(1)求甲、乙独做各需多少天?
(2)若从节省资金的角度,应该选择哪个工程队?
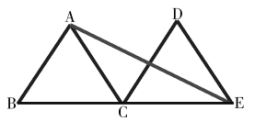
21.(8分)如图,![]() 是边长为2的等边三角形,将
是边长为2的等边三角形,将![]() 沿直线
沿直线![]() 平移到
平移到![]() 的位置,连接
的位置,连接![]() .
.
(1)求![]() 平移的距离;
平移的距离;
(2)求![]() 的长.
的长.
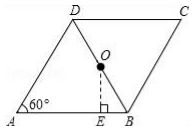
22.(10分)如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
(1)求∠ABD的度数;
(2)求线段BE的长.
23.(10分)某移动通信公司推出了如下两种移动电话计费方式,
| 月使用费/元 | 主叫限定时间/分钟 | 主叫超时费(元/分钟) |
方式一 | 30 | 600 | 0.20 |
方式二 | 50 | 600 | 0.25 |
说明:月使用费固定收取,主叫不超过限定时间不再收费,超过部分加收超时费.例如,方式一每月固定交费30元,当主叫计时不超过300分钟不再额外收费,超过300分钟时,超过部分每分钟加收0.20元(不足1分钟按1分钟计算)
(1)请根据题意完成如表的填空;
| 月主叫时间500分钟 | 月主叫时间800分钟 |
方式一收费/元 |
| 130 |
方式二收费/元 | 50 |
|
(2)设某月主叫时间为t(分钟),方式一、方式二两种计费方式的费用分别为y1(元),y2(元),分别写出两种计费方式中主叫时间t(分钟)与费用为y1(元),y2(元)的函数关系式;
(3)请计算说明选择哪种计费方式更省钱.
24.(12分)如图①,在平面直角坐标系中,直线y=−12x+2与![]() 交坐标轴于A,B两点.以AB为斜边在第一象限作等腰直角三角形ABC,C为直角顶点,连接OC.
交坐标轴于A,B两点.以AB为斜边在第一象限作等腰直角三角形ABC,C为直角顶点,连接OC.
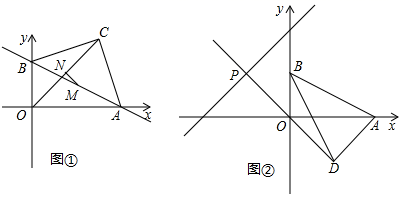
(1)求线段AB的长度
(2)求直线BC的解析式;
(3)如图②,将线段AB绕B点沿顺时针方向旋转至BD,且![]() ,直线DO交直线y=x+3
,直线DO交直线y=x+3![]() 于P点,求P点坐标.
于P点,求P点坐标.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、B
4、D
5、B
6、C
7、C
8、B
9、A
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、x≥﹣1.
12、①②③.
13、3
14、-1
15、4
16、①③④
三、解下列各题(本大题共8小题,共72分)
17、(1)y1=32x,y2=20x+600;(2)30≤x<50时,方案一划算.
18、(1)见解析;(2)![]() ;(3)
;(3)![]()
19、(1)![]() ;(2)四边形
;(2)四边形![]() 为菱形,理由详见解析;(3)以
为菱形,理由详见解析;(3)以![]() 为顶点的四边形是平行四边形时,点
为顶点的四边形是平行四边形时,点![]() 坐标
坐标![]() 或
或![]() 或
或![]()
20、(1)10 15 (2)选甲比较节约资金.
21、(1)2;(2)![]()
22、(1)∠ABD=60°;(3)BE=1.
23、(1)70;100;(2)详见解析;(3)当0≤t≤400时方式一省钱;当400<t≤1400时,方式二省钱,当t>1400时,方式一省钱,当为400分钟、1400分钟时,两种方式费用相同.
24、(1)![]() ;(2)
;(2)![]() ;(3)P点的坐标是
;(3)P点的坐标是![]() .
.
2023-2024学年福建省宁德市福鼎市九上数学期末学业水平测试试题含答案: 这是一份2023-2024学年福建省宁德市福鼎市九上数学期末学业水平测试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,如图,在菱形中,,且连接则,抛物线的对称轴是直线等内容,欢迎下载使用。
福建省宁德市福鼎市2023-2024学年数学八上期末统考模拟试题含答案: 这是一份福建省宁德市福鼎市2023-2024学年数学八上期末统考模拟试题含答案,共7页。试卷主要包含了数据5,7,8,8,9的众数是,下列各数中,是无理数,下列条件中能作出唯一三角形的是等内容,欢迎下载使用。
2022-2023学年重庆北碚区数学七下期末学业质量监测模拟试题含答案: 这是一份2022-2023学年重庆北碚区数学七下期末学业质量监测模拟试题含答案,共6页。试卷主要包含了下列各式计算正确的是,若分式的值为0,则x的值是,下列判断中,错误的是等内容,欢迎下载使用。












