2022-2023学年黑龙江省佳木斯市富锦市多校联考八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年黑龙江省佳木斯市富锦市多校联考八年级（下）期末数学试卷（含解析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 下列各式计算正确的是( )
A. 24÷ 6=4B. 54÷ 9= 6
C. 30÷ 6=5D. 47÷ 149=7 2
2. 满足下列条件的△ABC，其中不是直角三角形的是( )
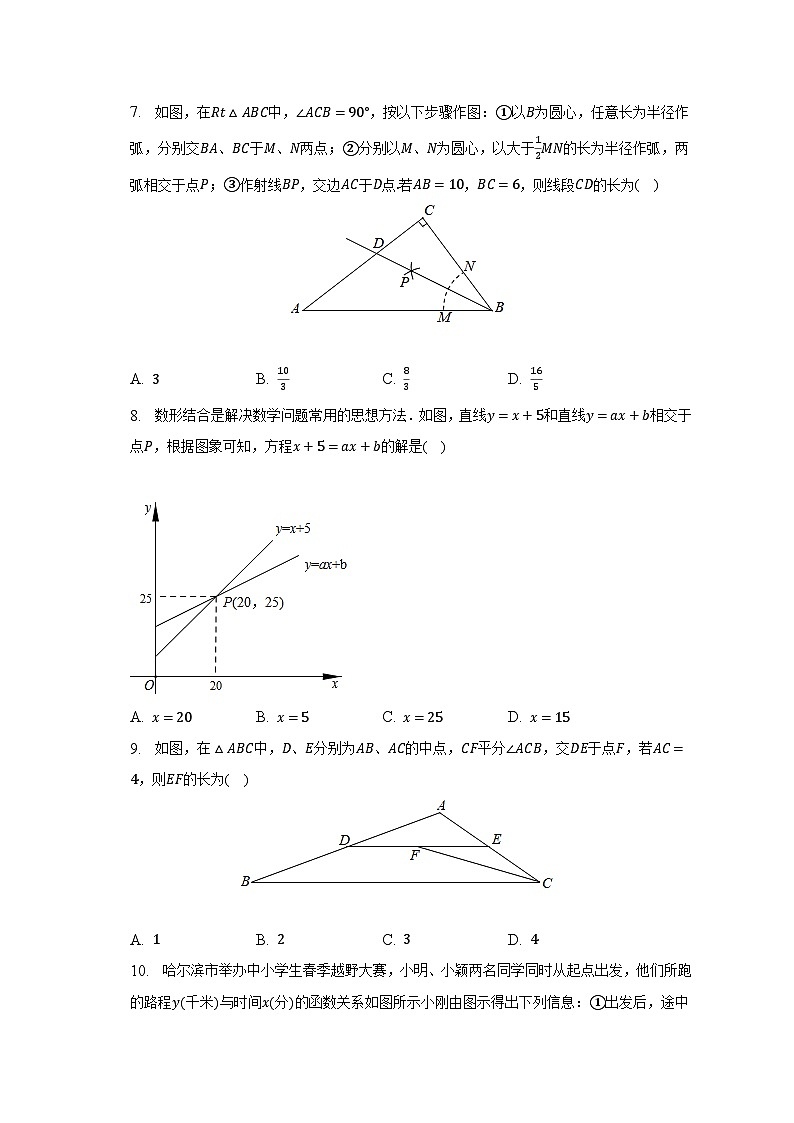
A. b2=(a+c)(a−c)B. a：b：c=1： 3：2
C. ∠C=∠A−∠BD. ∠A：∠B：∠C=3：4：5
3. 某校男子足球队的年龄分布如下表：
则这些队员年龄的平均数是( )
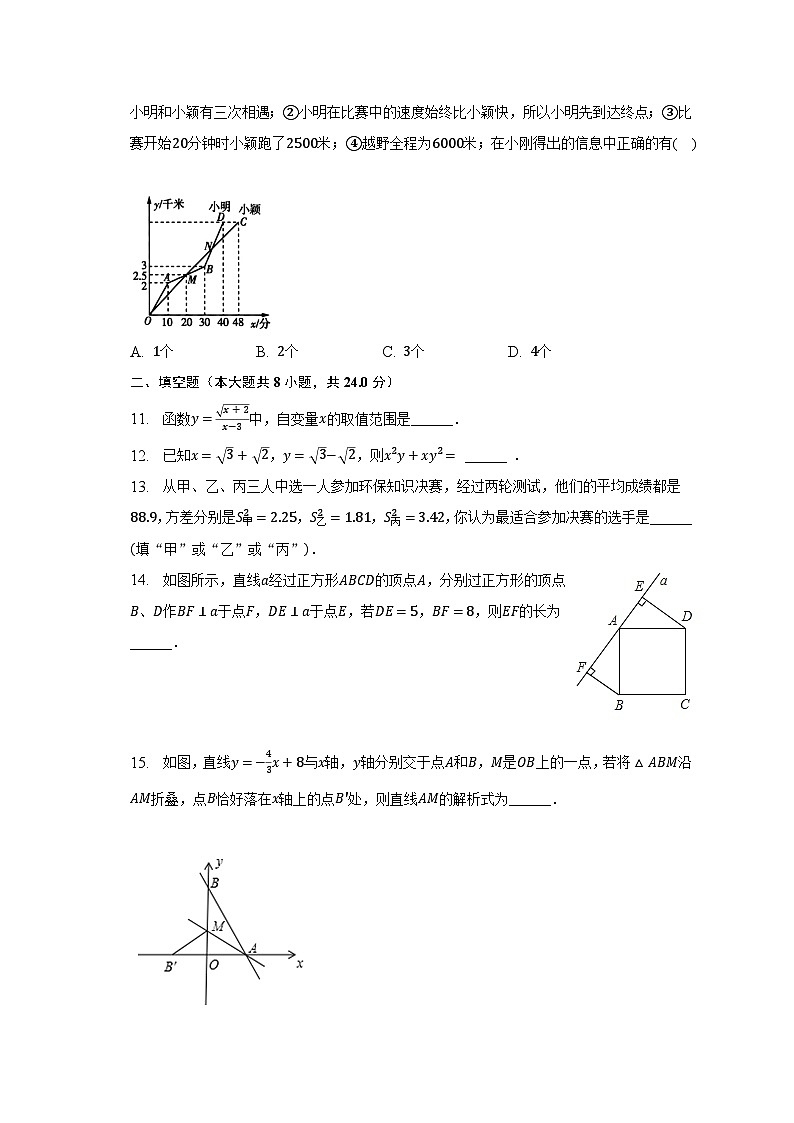
A. 13B. 14C. 14.5D. 15
4. 同一平面直角坐标系中，函数y=ax+b与y=bx+a的图象可能是( )
A. B. C. D.
5. 如图，在正方形ABCD中，点E是对角线上一点，连接AE，CE，若DE=AB，则∠AEC的度数为( )
A. 105°
B. 120°
C. 135°
D. 150°
6. 我们规定：对于任意的正数m，n的运算“Φ”为当mAB．
(1)作∠BAD的平分线交BC于点E，在AD上截取AF=AB，连接EF；(要求：尺规作图，保留作图痕迹，不写作法.)
(2)直接写出四边形ABEF的形状．
21. (本小题6.0分)
某校八年级甲、乙两班各有学生50人，为了解这两个班学生的身体素质情况，进行了抽样调查，过程如下，请补充完整．
(1)收集数据
从甲、乙两个班各随机抽取10名学生进行身体素质测试，测试成绩(百分制)如下：
甲班：65 75 75 80 60 50 75 90 85 65
乙班：90 55 80 70 55 70 95 80 65 70
(2)整理、描述数据
按如下分数段整理、描述这两组样本数据：
则m= ______ ，n= ______ ；
(3)分析数据
①两组样本数据的平均数、中位数、众数如下表：
则x= ______ ，y= ______ ．
②若规定测试成绩在80分以上的学生的身体素质为优秀，请估计乙班50名学生中身体素质为优秀的学生人数．
22. (本小题8.0分)
如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，求EF的长．
23. (本小题8.0分)
联想中垂线的性质，我们可引入如下概念：
定义：到三角形的两个顶点距离相等的点，叫做此三角形的“智慧心”．
(1)举例：如图①，在△ABC中，∠PAB=∠PBA，判断：点P ______ (填“是”或“不是”)△ABC的“智慧心”；
(2)应用：如图②，若CD为等边三角形ABC的高，“智慧心”P在高CD上，且PD=12AB，则∠APB的度数为______ ；
(3)探究：已知△ABC为直角三角形，∠A=90°，∠ABC=60°，AC=4，“智慧心”P在AC边上，则PA的长为______ ．
24. (本小题10.0分)
在近期“抗疫”期间，某药店销售A、B两种型号的口罩，已知销售80只A型和45只B型的利润为21元，销售40只A型和60只B型的利润为18元．
(1)求每只A型口罩和B型口罩的销售利润；
(2)该药店计划一次购进两种型号的口罩共2000只，其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍，设购进A型口罩x只，这2000只口罩的销售总利润为y元．
①求y关于x的函数关系式，并求出自变量x的取值范围；
②该药店购进A型、B型口罩各多少只，才能使销售总利润最大？
25. (本小题12.0分)
(1)【感知】如图①，四边形ABCD、CEFG均为正方形．BE与DG的数量关系为______．
(2)【拓展】如图②，四边形ABCD、CEFG均为菱形，且∠A=∠F.请判断BE与DG的数量关系，并说明理由
(3)【应用】如图③，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD延长线上．若AE=2ED，∠A=∠F，△EBC的面积为9，则菱形CEFG的面积为______．
26. (本小题12.0分)
如图所示，在平面直角坐标系中，四边形ABCD是菱形，点A的坐标为(−5,4)，点B，C在x轴上，点D在y轴上．
(1)求点B的坐标；
(2)动点P以每秒1个单位长度的速度从点O出发，沿射线OB方向运动，设点P运动的时间为t秒，连接PD，BD，设△PBD的面积为S(S≠0)，求S与t的函数关系式(请直接写出自变量t的取值范围)；
(3)在(2)的条件下，平面内是否存在点Q，使以A，C，P，Q为顶点的四边形为矩形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
答案和解析
1.【答案】B
【解析】解：A、 24÷ 6=2，不符合题意；
B、 54÷ 9= 6，符合题意；
C、 30÷ 6= 5，不符合题意；
D、 47÷ 149= 47×49=2 7，不符合题意；
故选：B．
根据二次根式的除法法则计算．
本题主要考查了二次根式的除法，掌握二次根式的除法运算法则是解题关键．
2.【答案】D
【解析】解：A、∵b2=(a+c)(a−c)，
∴b2=a2−c2即a2=c2+b2，
∴△ABC是直角三角形，故该选项不符合题意；
B、a：b：c=1： 3：2，设a=x,b= 3x,c=2x，
∴a2+b2=x2+3x2=4x2，c2=4x2，
∴a2+b2=c2，则△ABC是直角三角形，故该选项不符合题意；
C、∵∠C=∠A−∠B，∠C+∠B+∠A=180°，
∴2∠A=180°，
∴∠A=90°，
∴△ABC是直角三角形，故该选项不符合题意；
D、∠A：∠B：∠C=3：4：5，∠C+∠B+∠A=180°，
∴最大角为∠C=180°×53+4+5=75°，
∴△ABC不是直角三角形，故该选项符合题意；
故选：D．
根据勾股定理的逆定理，以及三角形的内角和定理进行计算即可解答．
本题考查了勾股定理的逆定理，三角形内角和定理，熟练掌握勾股定理的逆定理，以及三角形内角和定理是解题的关键．
3.【答案】C
【解析】解：平均数为(13×2+14×6+15×8+16×3+17×2+18×1)÷(2+6+8+3+2+1)=15(岁)，
故选：C．
根据平均数的意义和计算方法进行计算即可．
本题考查平均数，理解平均数的意义是正确解答的前提．
4.【答案】B
【解析】解：A，C选项中，两直线与y轴交于同一点，
∴a=b，
如果a=b，两条直线重合，不符合题意．
B选项中，两直线与y轴交点一个在x轴上方，一个在x轴下方，
∴a，b符号不同，符合题意．
D选项中，两条直线都是y随x增大而增大，则a，b都是正数，
∴两直线与y轴交点应该在x轴上方，不符合题意．
故选：B．
根据一次函数图象与系数的关系分别判断各选项．
本题考查一次函数的性质，解题关键是掌握一次函数图象与系数的关系．
5.【答案】C
【解析】解：∵四边形ABCD是正方形，
∴AD=DC=AB，∠ADB=∠EDC=45°，
在△ADE与△CDE中，
AD=CD∠ADB=∠EDCDE=DE，
∴△ADE≌△CDE(SAS)，
∴∠AED=∠CED，
∵DE=AB=AD，
∴∠AED=180°−45°2，
∴∠AEC=2∠AED=180°−45°=135°，
故选：C．
根据正方形的性质得出∠ADB=∠EDC，进而利用SAS证明△ADE与△CDE全等，利用全等三角形的性质和等腰三角形的性质解答即可．
此题考查正方形的性质，关键是根据正方形的性质得出∠ADB=∠EDC解答．
6.【答案】B
【解析】解：∵当m≥n时，mΦn=2 m− n，
∴3Φ2=2 3− 2，
∵当mS乙2，
∴最适合参加决赛的选手是乙．
故答案为：乙．
根据方差的定义，方差越小数据越稳定即可求解．
本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
14.【答案】13
【解析】解：∵四边形ABCD是正方形，
∴∠DAB=90°，AB=AD，
∵BF⊥a于点F，DE⊥a于点E，
∴∠DEA=∠BFA=∠BAD=90°，
∴∠BAF+∠DAE=90°，∠BAF+∠ABF=90°，
∴∠DAE=∠ABF，且AB=AD，∠DEA=∠BFA，
∴△ABF≌△DAE(SAS)
∴DE=AF=5，BF=AE=8，
∴EF=AF+AE=13，
故答案为：13．
由“SAS”可证△ABF≌△DAE，可得DE=AF=5，BF=AE=8，可得结论．
本题考查了正方形的性质，全等三角形的判定和性质，证明△ABF≌△DAE是本题的关键．
15.【答案】y=−12x+3
【解析】
【分析】
本题考查图形的翻折变换，待定系数法求解析式，勾股定理.解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
把x的值代入即可求出y的值，即是点的坐标，再把坐标代入就能求出解析式．
【解答】
解：法一：
当x=0时，y=−43x+8=8，即B(0,8)，
当y=0时，x=6，即A(6,0)，
所以AB=AB′=10，即B′(−4,0)，
因为点B与B′关于AM对称，
所以BB′的中点为(0−42,8+02)，即(−2,4)在直线AM上，
设直线AM的解析式为y=kx+b，把(−2,4)，(6,0)，代入可得：
y=−12x+3．
法二：
直线y=−43x+8与x轴，y轴分别交于点A和B，
∴A(6,0)，B(0,8)，
AB= 62+82=10，
∴AB′=10，
设OM=x，则B′M=BM=BO−MO=8−x，B′O=AB′−AO=10−6=4，
∴x2+42=(8−x)2，
x=3，
∴M(0,3)，
又A(6,0)，
直线AM的解析式为y=−12x+3．
故答案为y=−12x+3．
16.【答案】2.2
【解析】解：如图，过点A作AE⊥CD，则CE=AB=1.7，AE=BC= 6，AD=2.5，
Rt△ADE中，DE= AD2−AE2= (2.5)2−( 6)2=0.5，
∴CD=CE+ED=1.7+0.5=2.2．

故答案为：2.2．
如图，过点A作AE⊥CD，构建直角三角形，运用勾股定理求解．
本题考查勾股定理解直角三角形，关键是添加辅助线构造直角三角形．
17.【答案】245
【解析】解：∵四边形ABCD是菱形，
∴BO=DO=4，AO=CO，AC⊥BD，
∴BD=8，
∵S菱形ABCD=12AC×BD=24，
∴AC=6，
∴OC=12AC=3，
∴BC= OB2+OC2=5，
∵S菱形ABCD=BC×AH=24，
∴AH=245；
故答案为：245．
根据菱形面积=对角线积的一半可求AC，再根据勾股定理求出BC，然后由菱形的面积即可得出结果．
本题考查了菱形的性质、勾股定理以及菱形面积公式；熟练掌握菱形的性质，由勾股定理求出BC是解题的关键．
18.【答案】2n−1 3
【解析】解：∵四边形A0B1A1C1菱形，
∴A1B1=B1A0=2，
又∵∠A0B1A1=60°，
∴△A1B1A0是等边三角形，
∴点B1的横坐标为 3，
同理可求点B2的横坐标为2 3，点B3的横坐标为4 3，点B4的横坐标为8 3，
∴点Bn的横坐标为2n−1 3，
故答案为：2n−1 3．
由菱形的性质可得A1B1=B1A0=2，可证△A1B1A0是等边三角形，可得点B1的横坐标为 3，同理可证点B2的横坐标为2 3，点B3的横坐标为4 3，点B4的横坐标为8 3，即可求解．
本题考查了菱形的性质，等边三角形的性质，找出规律是解题的关键．
19.【答案】解：原式=(5x+3yx2−y2−2xx2−y2)÷1x2y−xy2
=5x+3y−2xx2−y2⋅(x2y−xy2)
=3(x+y)(x+y)(x−y)⋅xy(x−y)
=3xy．
当x= 5+1，y= 5−1时，
原式=3×( 5+1)( 5−1)
=3×(5−1)
=12．
【解析】先将分式化简，再代值计算即可．
本题考查分式的化简求值．正确化简是解题的关键．
20.【答案】解：(1)如图所示．

(2)四边形ABEF是菱形．理由如下：
∵四边形ABCD是平行四边形，
∴AD//BC．
∴∠DAE=∠AEB．
∵AE平分∠BAD，
∴∠BAE=∠DAE．
∴∠BAE=∠AEB，
∴BE=AB．
由(1)得AF=AB，
∴BE=AF．
又∵BE//AF，
∴四边形ABEF是平行四边形．
∵AF=AB，
∴四边形ABEF是菱形．
【解析】(1)以点A为圆心，适当长度为半径画弧，交AB、AD于两点；分别以两点为圆心，适当长度为半径画弧，两弧交于一点，连接该点与A点交BC于点E，以点A为圆心，AB长为半径画弧，交AD于点F，连接EF．
(2)由平行四边形的性质和角平分线得出∠BAE=∠AEB，证出BE=AB，由(1)得：AF=AB，得出BE=AF，即可得出结论．
本题考查了平行四边形的性质、作图一基本作图、等腰三角形的判定、菱形的判定；熟练掌握平行四边形的性质和角平分线作图，证明BE=AB是解决问题(2)的关键．
21.【答案】3 2 75 70
【解析】解：(2)由收集的数据可得：m=3，n=2，
故答案为：3，2；
(3)①加班成绩为：50，60，65，65，75，75，75，80，85，90，
∴甲班成绩的中位数x=75+752=75，
乙班成绩出现次数最多的是7(0分)，
∴乙班成绩的众数为y=70，
故答案为：75，70；
②根据题意得：50×410=20(名)，
答：估计乙班50名学生中身体素质为优秀的学生为20名．
(2)由收集的数据即可得到答案；
(3)①由众数和中位数的定义求解可得；②用总人数乘以乙班样本中优秀人数所占比例可得．
本题考查了众数、中位数以及样本估计总体，熟练掌握众数、中位数的定义以及用样本估计总体的计算方法是解题的关键．
22.【答案】解：由图形折叠可得BE=EG，DF=FG，
∵正方形ABCD的边长为3，BE=1，
∴EG=1，EC=3−1=2，CF=3−FG，
在直角△ECF中，
∴EF2=EC2+CF2，
∴(1+GF)2=22+(3−GF)2，
解得GF=32，
∴EF=1+32=52．
【解析】由图形折叠可得BE=EG，DF=FG，因为正方形ABCD的边长为3，BE=1，求出EG，EC，在直角△ECF中，运用勾股定理求出GF，再求出EF．
本题主要考查了折叠问题，解题的关键是找准不变的线段，利用勾股定理求解线段．
23.【答案】是 90° 2或43
【解析】解：(1)∵∠PAB=∠PBA，
∴PA=PB，
∴点P是△ABC的“智慧心”，
故答案为：是；
(2)连接PA、PB，

若PB=PC，则∠PCB=∠PBC，
∵CD为等边三角形ABC的高，
∴AD=BD，∠PCB=30°，
∴∠PBD=∠PBC=30°，
∴PD= 33DB= 36AB，这与已知PD=12AB矛盾，
∴PB≠PC，即PB=PC不存在，
同理可知，PA≠PC，即PA=PC不存在，
若PA=PB，
∵PD=12AB，
∴PD=BD，
∴∠BPD=45°，
∴∠APB=90°，
故答案为：90°；
(3)若PB=PC，设PC=x，则PA=4−x，

∵∠A=90°，∠ABC=60°，
∴∠ACB=30°，
∴BC=2AB，
由勾股定理得：AB2+AC2=BC2，即AB2+42=(2AB)2，
解得：AB=4 33，
在Rt△BAP中，BP2=PA2+AB2，即x2=(4−x)2+(4 33)2，
解得：x=83，
∴PA=4−83=43；
若PA=PC，则PA=12AC=2，
若PA=PB，由图知，在Rt△PBC中，这种情况不可能，
综上所述，PA的长为2或43，
故答案为：2或43．
(1)根据等腰三角形的判定定理得到PA=PB，根据“智慧心”的定义判断；
(2)分PB=PC、PA=PC、PA=PB三种情况，根据等边三角形的性质和“智慧心”的定义解答；
(3)根据勾股定理求出PB=PC、PA=PC、PA=PB三种情况，根据勾股定理解答．
本题考查了等边三角形的性质，直角三角形的性质，勾股定理的应用，理解“智慧心”的定义是解题的关键．
24.【答案】解：(1)设每只A型口罩销售利润为a元，每只B型口罩销售利润为b元，根据题意得：
80a+45b=2140a+60b=18，
解得a=0.15b=0.2，
答：每只A型口罩销售利润为0.15元，每只B型口罩销售利润为0.2元；
(2)①根据题意得，y=0.15x+0.2(2000−x)，即y=−0.05x+400；
根据题意得，2000−x≥x2000−x≤3x，解得500≤x≤1000，
∴y=−0.05x+400(500≤x≤1000)；
②∵y=−0.05x+400，k=−0.05