人教版九年级上册第22章《二次函数》单元测试卷
展开
这是一份人教版九年级上册第22章《二次函数》单元测试卷,共6页。
人教版九年级上册第22章《二次函数》单元测试卷一.选择题(共10小题,满分30分,每小题3分)1.下列函数中属于二次函数的是( )A.y=x(x+1) B.x2y=1 C.y=2x2﹣2(x2+1) D.y=![]() 2.二次函数y=
2.二次函数y=![]() x2+3x+
x2+3x+![]() 化为y=(x﹣h)2+k的形式,结果正确的是( )A.
化为y=(x﹣h)2+k的形式,结果正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.二次函数y=﹣x2﹣8x+c的最大值为0,则c的值等于( )A.4 B.﹣4 C.﹣16 D.164.二次函数的图象如图所示,则其解析式是( )
3.二次函数y=﹣x2﹣8x+c的最大值为0,则c的值等于( )A.4 B.﹣4 C.﹣16 D.164.二次函数的图象如图所示,则其解析式是( )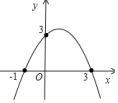 A.y=﹣x2+2x+3 B.y=x2﹣2x﹣3 C.y=﹣x2﹣2x+3 D.y=﹣x2﹣2x﹣35.在同一坐标系中,抛物线y=4x2,y=
A.y=﹣x2+2x+3 B.y=x2﹣2x﹣3 C.y=﹣x2﹣2x+3 D.y=﹣x2﹣2x﹣35.在同一坐标系中,抛物线y=4x2,y=![]() x2,y=﹣
x2,y=﹣![]() x2的共同特点是( )A.关于y轴对称,开口向上 B.关于y轴对称,y随x的增大而增大 C.关于y轴对称,y随x的增大而减小 D.关于y轴对称,顶点是原点6.将抛物线y=x2﹣2向右平移1个单位长度后,所得抛物线的解析式为( )A.y=(x+1)2﹣2 B.y=(x﹣1)2﹣2 C.y=(x+2)2+1 D.y=(x﹣2)2+17.已知一次函数y=
x2的共同特点是( )A.关于y轴对称,开口向上 B.关于y轴对称,y随x的增大而增大 C.关于y轴对称,y随x的增大而减小 D.关于y轴对称,顶点是原点6.将抛物线y=x2﹣2向右平移1个单位长度后,所得抛物线的解析式为( )A.y=(x+1)2﹣2 B.y=(x﹣1)2﹣2 C.y=(x+2)2+1 D.y=(x﹣2)2+17.已知一次函数y=![]() x+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )
x+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )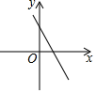 A.
A.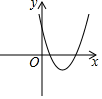 B.
B.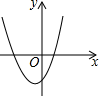 C.
C.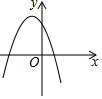 D.
D.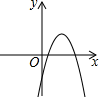 8.将一根长为50cm的铁丝弯成一个长方形(铁丝全部用完且无损耗)如图所示,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( )
8.将一根长为50cm的铁丝弯成一个长方形(铁丝全部用完且无损耗)如图所示,设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数关系式为( ) A.y=﹣x2+50x B.y=x2﹣50x C.y=﹣x2+25x D.y=﹣2x2+259.已知二次函数y=kx2﹣7x﹣7的图象与x轴有两个交点,则k的取值范围为( )A.k>﹣
A.y=﹣x2+50x B.y=x2﹣50x C.y=﹣x2+25x D.y=﹣2x2+259.已知二次函数y=kx2﹣7x﹣7的图象与x轴有两个交点,则k的取值范围为( )A.k>﹣![]() B.k>﹣
B.k>﹣![]() 且k≠0 C.k≥﹣
且k≠0 C.k≥﹣![]() D.k≥﹣
D.k≥﹣![]() 且k≠010.已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
且k≠010.已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )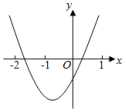 A.4个 B.3个 C.2个 D.1个二.填空题(共6小题,满分18分,每小题3分)11.若函数y=(m2+m)
A.4个 B.3个 C.2个 D.1个二.填空题(共6小题,满分18分,每小题3分)11.若函数y=(m2+m)![]() 是二次函数,则m= .12.抛物线y=2x2+3x+k﹣2经过点(﹣1,0),那么k= .13.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是 .(请用“>”连接排序)
是二次函数,则m= .12.抛物线y=2x2+3x+k﹣2经过点(﹣1,0),那么k= .13.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是 .(请用“>”连接排序)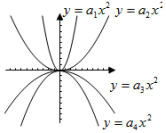 14.如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为 米.
14.如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为 米.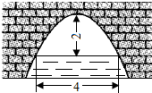 15.已知二次函数y=﹣4x2﹣8ax﹣a2+2a,当﹣1≤x≤1时,y的最大值为5,那么a的值为 .16.如图,函数
15.已知二次函数y=﹣4x2﹣8ax﹣a2+2a,当﹣1≤x≤1时,y的最大值为5,那么a的值为 .16.如图,函数![]() 的图象,若直线y=x+m与该图象只有一个交点,则m的取值范围为 .
的图象,若直线y=x+m与该图象只有一个交点,则m的取值范围为 .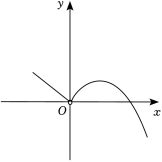 三.解答题(共6小题,满分52分)17.(6分)已知抛物线y=ax2经过点A(﹣2,﹣8).(1)求此抛物线的函数解析式;(2)写出这个二次函数图象的顶点坐标、对称轴;(3)判断点B(﹣1,﹣4)是否在此抛物线上;(4)求出此抛物线上纵坐标为﹣6的点的坐标. 18.(8分)(1)请在坐标系中画出二次函数y=x2﹣2x﹣1的大致图象.(2)根据方程的根与函数图象之间的关系.将方程x2﹣2x﹣1=0的根在图上近似的表示出来;(描点)(3)观察图象,直接写出方程x2﹣2x﹣1=0的根.(精确到0.1)
三.解答题(共6小题,满分52分)17.(6分)已知抛物线y=ax2经过点A(﹣2,﹣8).(1)求此抛物线的函数解析式;(2)写出这个二次函数图象的顶点坐标、对称轴;(3)判断点B(﹣1,﹣4)是否在此抛物线上;(4)求出此抛物线上纵坐标为﹣6的点的坐标. 18.(8分)(1)请在坐标系中画出二次函数y=x2﹣2x﹣1的大致图象.(2)根据方程的根与函数图象之间的关系.将方程x2﹣2x﹣1=0的根在图上近似的表示出来;(描点)(3)观察图象,直接写出方程x2﹣2x﹣1=0的根.(精确到0.1)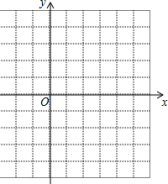 19.(8分)如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,(1)求抛物线的解析式;(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?
19.(8分)如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,(1)求抛物线的解析式;(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?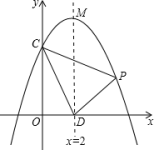 20.(8分)设二次函数y1=nx2+mx+n﹣5(m,n为常数,n≠0)且m+2n=3.(1)若该二次函数的图象过点(2,4),求二次函数的表达式;(2)函数y1的图象始终过一个定点M,求点M的坐标.(3)已知点P(x0,a)与Q(1,b)都在函数y1的图象上,若x0<1时,a>b,求x0的取值范围(用含n的代数式表示). 21.(10分)我市“佳禾”农场的十余种有机蔬菜在北京市场上颇具竞争力.某种有机蔬菜上市后,一经销商在市场价格为10元/千克时,从“佳禾”农场收购了某种有机蔬菜2000 千克存放入冷库中.据预测,该种蔬菜的市场价格每天每千克将上涨0.2元,但冷库存放这批蔬菜时每天需要支出各种费用合计148元,已知这种蔬菜在冷库中最多保存90天,同时,平均每天将会有6千克的蔬菜损坏不能出售.(1)若存放x天后,将这批蔬菜一次性出售,设这批蔬菜的销售总金额为y元,试写出y与x之间的函数关系式.(2)经销商想获得利润7200元,需将这批蔬菜存放多少天后出售?(利润=销售总金额﹣收购成本﹣各种费用)(3)经销商将这批蔬菜存放多少天后出售可获得最大利润?最大利润是多少? 22.(12分)如图,在平面直角坐标系中,直线y=﹣
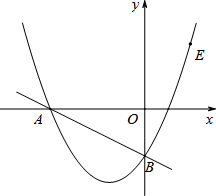
20.(8分)设二次函数y1=nx2+mx+n﹣5(m,n为常数,n≠0)且m+2n=3.(1)若该二次函数的图象过点(2,4),求二次函数的表达式;(2)函数y1的图象始终过一个定点M,求点M的坐标.(3)已知点P(x0,a)与Q(1,b)都在函数y1的图象上,若x0<1时,a>b,求x0的取值范围(用含n的代数式表示). 21.(10分)我市“佳禾”农场的十余种有机蔬菜在北京市场上颇具竞争力.某种有机蔬菜上市后,一经销商在市场价格为10元/千克时,从“佳禾”农场收购了某种有机蔬菜2000 千克存放入冷库中.据预测,该种蔬菜的市场价格每天每千克将上涨0.2元,但冷库存放这批蔬菜时每天需要支出各种费用合计148元,已知这种蔬菜在冷库中最多保存90天,同时,平均每天将会有6千克的蔬菜损坏不能出售.(1)若存放x天后,将这批蔬菜一次性出售,设这批蔬菜的销售总金额为y元,试写出y与x之间的函数关系式.(2)经销商想获得利润7200元,需将这批蔬菜存放多少天后出售?(利润=销售总金额﹣收购成本﹣各种费用)(3)经销商将这批蔬菜存放多少天后出售可获得最大利润?最大利润是多少? 22.(12分)如图,在平面直角坐标系中,直线y=﹣![]() x﹣2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.(1)求抛物线的解析式;(2)E为抛物线上第一象限部分上一点,当S△ABE=10时,求点E的坐标;(3)F为直线AB下方抛物线上一点,连接AF,当∠FAB=∠BAO时,求F点坐标.
x﹣2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.(1)求抛物线的解析式;(2)E为抛物线上第一象限部分上一点,当S△ABE=10时,求点E的坐标;(3)F为直线AB下方抛物线上一点,连接AF,当∠FAB=∠BAO时,求F点坐标.