2022-2023学年山东省滨州市滨城区七年级（下）期末数学试卷（含解析）

这是一份2022-2023学年山东省滨州市滨城区七年级（下）期末数学试卷（含解析），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 如图，直线a//b，∠1=40°，则∠2=( )
A. 130°
B. 140°
C. 150°
D. 160°
2. 下列说法不正确的是( )
A. 0的平方根是0
B. (−2)2 的平方根是2
C. 正数的平方根互为相反数
D. 一个正数的算术平方根一定大于这个数的相反数
3. 如图，下列结论中不正确的是( )
A. 若AD//BC，则∠1=∠B
B. 若∠1=∠2，则AD//BC
C. 若∠2=∠C，则AE//CD
D. 若AE//CD，则∠1+∠3=180°
4. 下列说法不成立的是( )
A. 若ac2y，则−a2x<−a2y
C. 若ac2b，则2−a<2−b
5. 在解二元一次方程组x−2y=2①4x−2y=5②时，下列方法中无法消元的是( )
A. ①−②
B. 由①变形得x=2+2y③，将③代入②
C. ①×4+②
D. 由②变形得2y=4x−5③，将③代入①
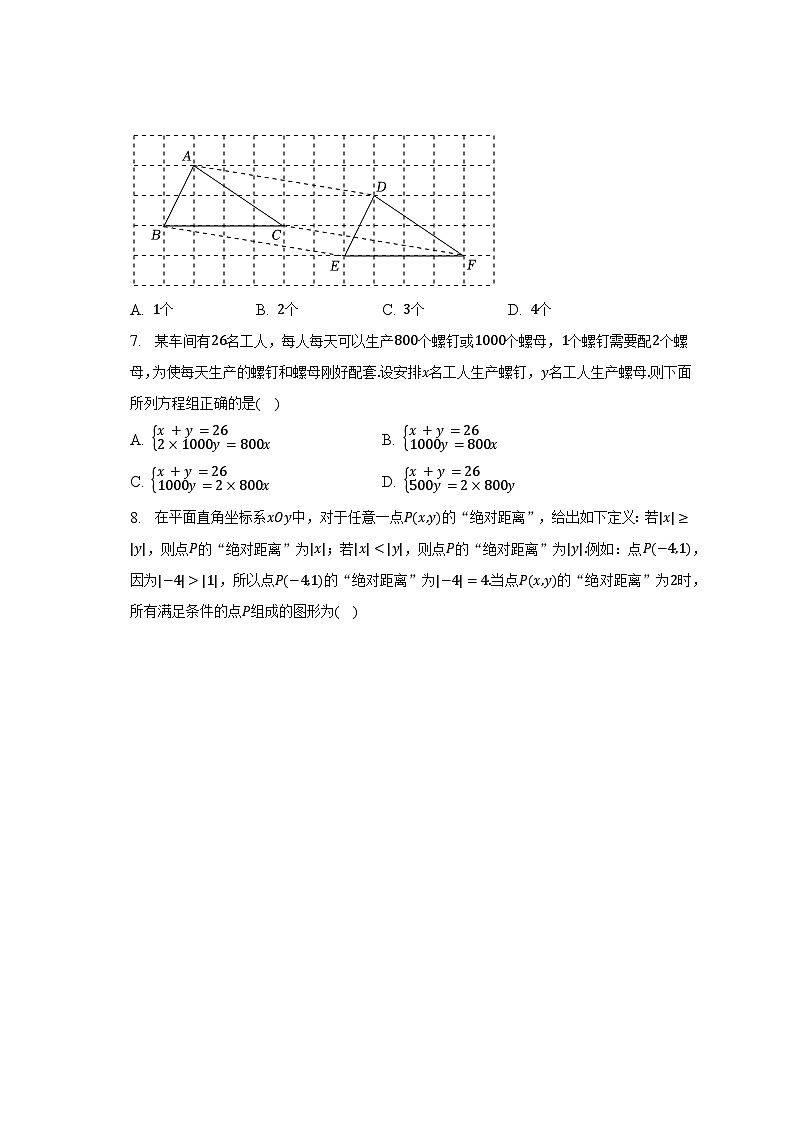
6. 如图，△ABC平移到△DEF的位置，则下列说法：①AD=CF=BE；②∠ACF+∠DAC=180°；③平移的方向是点C到点E的方向；④四边形ACFD，BCFE，ABED为平行四边形.其中说法正确的有( )
A. 1个B. 2个C. 3个D. 4个
7. 某车间有26名工人，每人每天可以生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套.设安排x名工人生产螺钉，y名工人生产螺母.则下面所列方程组正确的是( )
A. x+y=262×1000y=800xB. x+y=261000y=800x
C. x+y=261000y=2×800xD. x+y=26500y=2×800y
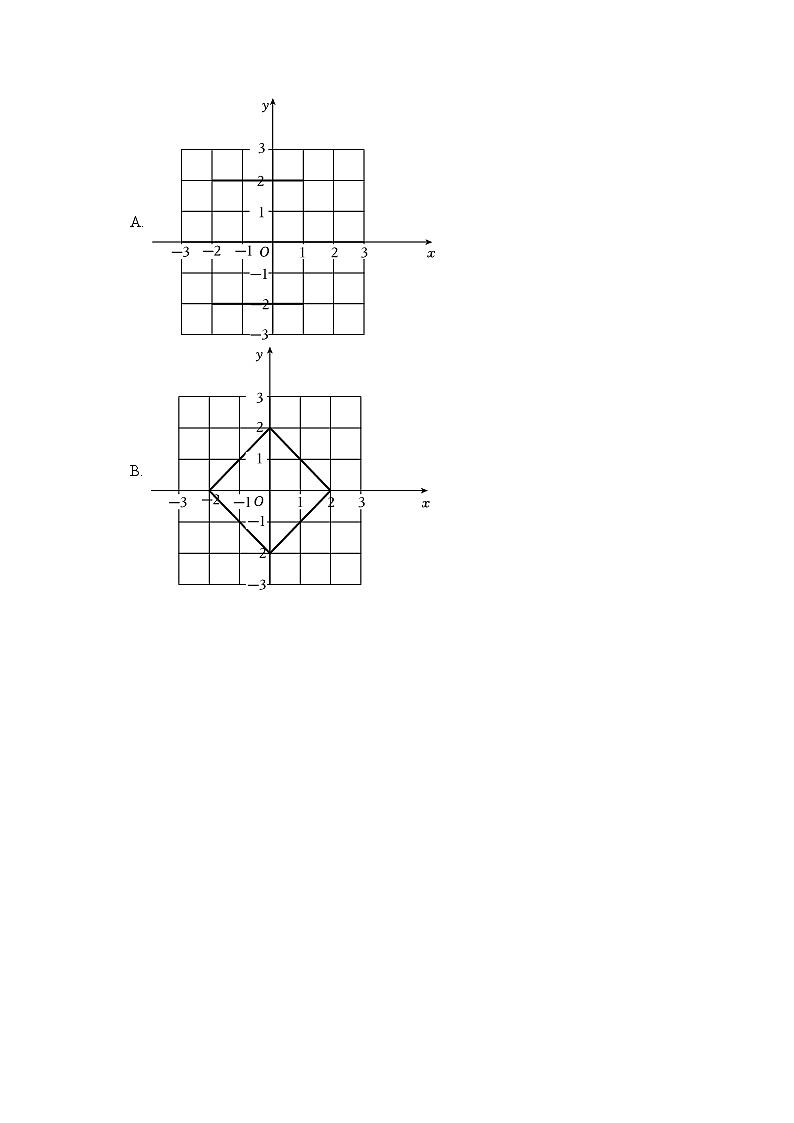
8. 在平面直角坐标系xOy中，对于任意一点P(x,y)的“绝对距离”，给出如下定义：若|x|≥|y|，则点P的“绝对距离”为|x|；若|x|<|y|，则点P的“绝对距离”为|y|.例如：点P(−4,1)，因为|−4|>|1|，所以点P(−4,1)的“绝对距离”为|−4|=4.当点P(x,y)的“绝对距离”为2时，所有满足条件的点P组成的图形为( )
A.
B.
C.
D.
二、填空题（本大题共8小题，共24.0分）
9. 已知点P(2−a,−5)，则点P到y轴的距离是______ ．
10. 2023年5月30日9时31分，搭载神舟十六号载人飞船的长征二号F遥十六运载火箭在酒泉卫星发射中心发射升空，航天员乘组状态良好，发射取得圆满成功.神舟十六号航天员乘组由景海鹏、朱杨柱、桂海潮3名航天员组成.发射前，科学家对飞船实施检查，最适宜的检查方式是______ (填“全面调查”或“抽样调查”)．
11. 如图所示，∠AOB的一边OB为平面镜，∠AOB=40°，一束光线(与水平线AO平行)从点C射入经平面镜上的点D后，反射光线落在OA上的点E处，则∠BCD的度数______ ．
12. 如图，已知直线l上，点P为直线l外一点，点B为直线l上的动点，PB≥4cm，则点P到直线l的距离是______ ．
13. 若关于x的不等式组2x−a<01−2x≥7的解集是x≤−3，则实数a的取值范围是______ ．
14. 关于x，y方程组2x+y=5x−2y=m的解也是方程2x−3y=1的解，则m= ______ ．
15. 已知平面直角坐标系中，A(3,4)，B(−2,1)，C(1,0)，延长AB与x轴交于一点P，若S△PBC=13S△ABC，则P点的坐标为______ ．
16. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等，例如图(1)就是一个幻方.图(2)是一个未完成的幻方，则x与y的和是______ ．
(1)
(2)
三、解答题（本大题共7小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题12.0分)
(1)计算：−32+ 25+|−1|−3−8；
(2)解二元一次方程组：3x−y+1=03x−y+43+2y=5；
(3)解不等式组：13x−1≤3−53xx−71518. (本小题10.0分)
2023年3月22日是第三十一届“世界水日”，某校举行了水资源保护知识竞赛.为了了解本次知识竞赛成绩的分布情况，从参赛学生中随机抽取了150名学生的初赛成绩进行统计，得到如下两幅不完整的统计图表．
(1)表中a= ______ ，b= ______ ，c= ______ ；
(2)请补全频数分布直方图；
(3)若该校共有360名学生，估计在知识竞赛中取得90分以上的学生大约有多少名？
19. (本小题10.0分)
已知∠1=∠2，∠3=∠4，∠5=∠A，试说明：BE//CF．
请完善下面解答过程，并填写理由．
解：∵∠3=∠4(已知)，
∴AE// ( )，
∴∠EDC= (两直线平行，内错角相等)，
∵∠5=∠A(已知)，
∴∠EDC= ( )，
∴DC//AB(同位角相等，两直线平行)，
∴∠5+∠ABC=180°( )，
即∠5+∠2+∠3=180°，
∵∠1=∠2(已知)，
∴∠5+∠1+∠3=180°(等量代换)，
即∠BCF+∠3=180°，
∴BE// ( ).
20. (本小题8.0分)
问题背景：
(1)已知点A(1,2)，B(5,2)，C(−1,−1)，D(3,−3)，在平面直角坐标系中描出这几个点，并分别找到线段AB和CD的中点M，N，然后写出它们的坐标，则点M为______ ，点N为______ ；
尝试应用：
(2)①结合上述结果，我们可以发现如果线段的两个端点坐标分别为(a,b)，(c,d)，则这条线段的中点坐标为______ ；
②若点P(−3,7)，Q(1,−3)，用我们发现的结论可以直接得到线段PQ的中点坐标为______ ．
21. (本小题12.0分)
已知：现有A型车和B型车载满货物一次可运货情况如表：
某物流公司现有35吨货物，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物．根据以上信息，解答下列问题：
(1)1辆A型车和1辆B型车都载满货物一次可分别运货多少吨？
(2)请你帮该物流公司设计租车方案；
(3)若A型车每辆需租金300元/次，B型车每辆需租金320元/次，请选出最省钱的租车方案，并求出最少租车费．
22. (本小题14.0分)
在平面直角坐标系中，点A(2,a)，B(b,2)，若a，b满足 3a−b−6+(a−b+2)2=0．

(1)求点A，B的坐标；
(2)如图1，连接OA，OB，求△OAB的面积；
(3)如图2，3将线段AB平移到EF，
①若点E在y轴上，点F在x轴上，点C(m,n)在线段EF上，试确定m，n应满足什么关系式？
②若点E在x轴上，点F在y轴上，点D在直线EF上，且点D的纵坐标为t，当满足12S△DOE≥23S△AOB时，求t的取值范围．
23. (本小题6.0分)
在人教版七年级上、下册分别学习了《一元一次方程》和《二元一次方程组》，请叙述学习“方程”的研究路径，并猜想在以后学习，我们还将学习哪些方程？请举例．
答案和解析
1.【答案】B
【解析】解：如图所示，

∵a//b，∠1=40°，
∴∠3=∠1=40°，
∴∠2=180°−∠3=140°，
故选：B．
根据平行线的性质得出∠3=∠1=40°，然后根据邻补角互补即可求解．
本题考查了平行线的性质，熟练掌握平行线的性质是解题的关键．
2.【答案】B
【解析】解：∵0的平方根是0，
∴选项A不符合题意；
∵(−2)2 的平方根是±2，
∴选项B符合题意；
∵正数的平方根互为相反数，
∴选项C不符合题意；
∵一个正数的算术平方根一定大于这个数的相反数，
∴选项D不符合题意，
故选：B．
运用平方根的知识进行逐一辨别、求解．
此题考查了运用平方根进行有关运算的能力，关键是能准确理解并运用以上知识．
3.【答案】A
【解析】解：A、∵AD//BC，
∴∠1=∠2，
∵∠2≠∠B，
∴∠1≠∠B，
故A符合题意；
B、∵∠1=∠2，
∴AD//BC(内错角相等，两直线平行)，
故B不符合题意；
C、∵∠2=∠C，
∴AE//CD(同位角相等，两直线平行)，
故C不符合题意；
D、∵AE//CD，
∴∠1+∠3=180°(两直线平行，同旁内角互补)，
故D不符合题意；
故选：A．
根据平行线的性质即可判断A和D；根据平行线的判定，即可判断B和C，即可解答．
本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解题的关键．
4.【答案】B
【解析】解：∵ac2∴c2>0，
∴根据不等式的性质2，得a∴选项A不符合题意；
∵x>y，−a2=0时，
−a2x<−a2y不成立，
∴选项B符合题意；
∵ac2∴c2>0，
∴根据不等式的性质2，得a∴选项C不符合题意；
∵a>b，
∴根据不等式的性质3，得−a<−b，
∴根据不等式的性质1，得2−aa<2−b，
∴选项D不符合题意，
故选：B．
运用不等式的性质进行逐一辨别、求解．
此题考查了不等式性质的应用能力，关键是能准确理解并运用该知识进行变形、求解．
5.【答案】C
【解析】解：A.①−②，可以消去y，故A不符合题意；
B.由①变形得x=2+2y③，将③代入②，可以消去x，故B不符合题意；
C.①×4+②，无法消元，故C符合题意；
D.由②变形得2y=4x−5③，将③代入①，可以消去y，故D不符合题意；
故选：C．
利用加减消元法和代入消元法，进行计算逐一判断即可解答．
本题考查了解二元一次方程组，熟练掌握加减消元法和代入消元法是解题的关键．
6.【答案】C
【解析】解：①由平移的性质可知，AD=CF=BE，因此①正确；
②由平移的性质可知，AD//CF，∴∠ACF+∠DAC=180°，因此②正确；
③平移的方向是点C到点F的方向，因此③不正确；
④由平移的性质可得，AB//DE，AD//CF//BE，AC//DF，所以四边形ACFD，BCFE，ABED为平行四边形，因此④正确；
综上所述，正确的有①②④，共3个，
故选：C．
根据平移的性质，平行线的性质和判断，平行四边形的判定逐项进行判断即可．
本题考查平移的性质，平行线的性质以及平行四边形的判定，掌握平移的性质是正确解答的关键．
7.【答案】C
【解析】解：由题意可得，x+y=26 1000y=2×800x ，
故选：C．
根据车间有26名工人，可得x+y=26，根据1个螺钉需要配两个螺母，可得到1000y=2×800x，然后即可列出相应的方程组．
本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．
8.【答案】D
【解析】解：∵点P(x,y)的“绝对距离”为2，
∴|x|=2，|y|≤2或|y|=2，|x|≤2，
即x=2时，−2≤y≤2，x=−2时，−2≤y≤2，y=2时，−2≤x≤2，y=−2时，−2≤x≤2，
即可确定点P组成的图形为图D中的正方形，
故选：D．
根据点P(x,y)的“绝对距离”为2，可知|x|=2，|y|≤2或|y|=2，|x|≤2，即可确定点P组成的图形．
本题考查了点的坐标，新定义，理解新定义是解题的关键．
9.【答案】|2−a|
【解析】解：已知点P(2−a,−5)，则点P到y轴的距离是|2−a|，
故答案为：|2−a|．
根据点到y轴的距离等于横坐标的绝对值，即可解答．
本题考查了点的坐标，熟练掌握点到y轴的距离等于横坐标的绝对值是解题的关键．
10.【答案】全面调查
【解析】解：2023年5月30日9时31分，搭载神舟十六号载人飞船的长征二号F遥十六运载火箭在酒泉卫星发射中心发射升空，航天员乘组状态良好，发射取得圆满成功．神舟十六号航天员乘组由景海鹏、朱杨柱、桂海潮3名航天员组成．发射前，科学家对飞船实施检查，最适宜的检查方式是全面调查．
故答案为：全面调查．
一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
本题考查了全面调查与抽样调查，由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
11.【答案】40°
【解析】解：∵CD//AO，
∴∠BCD=∠AOB，
∵∠AOB=40°，
∴∠BCD=40°，
故答案为：40°．
根据“两直线平行，同位角相等”求解即可．
此题考查了平行线的性质，熟记平行线的性质定理是解题的关键．
12.【答案】4cm
【解析】解：点B为直线l上的动点，PB≥4cm，则点P到直线l的距离是4cm．
故答案为：4cm．
直线外一点到直线的垂线段的长度，叫做点到直线的距离，由此即可得到答案．
本题考查点到直线的距离，关键是掌握点到直线的距离的定义．
13.【答案】a>−6
【解析】解：2x−a<0①1−2x≥7②，
解不等式①得：x解不等式②得：x≤−3，
∵关于x的不等式组的解集是x≤−3，
∴a2>−3，
故答案为：a>−6．
首先解每个不等式，然后根据不等式组的解集，即可求得答案．
本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
14.【答案】0
【解析】解：∵x、y满足方程组2x+y=5x−2y=m和方程2x−3y=1，
∴联立2x+y=52x−3y=1，
解得，x=2y=1，
将其代入x−2y=m，
得，2−2=m，
∴m=0，
故答案为：0．
由于x、y满足方程组2x+y=5x−2y=m和方程2x−3y=1，解方程组2x+y=52x−3y=1，即可得出m的值．
本题主要考查二元一次方程组的解，联立方程组，得出正确的解是解题的关键．
15.【答案】(−113,0)
【解析】解：过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，如图所示：
∵A(3,4)，B(−2,1)，C(1,0)，
∴BE=1，EC=1−(−2)=3，CD=3−1=2，DE=3−(−2)=5，AD=4，
∴S△ABC=S梯形ABED−S△BCE−S△ACD=12×(1+4)×5−12×1×3−12×2×4=7，
∴S△PBC=13×7=73，
设点P的坐标为(m,0)，
∵C(1,0)，
∴CP=1−m，
∴12(1−m)=73，
解得：m=−113，
∴点P的坐标为(−113,0)．
故答案为：(−113,0)．
过点A作AD⊥x轴于点D，过点B作BE⊥x轴于点E，根据A(3,4)，B(−2,1)，C(1,0)，求出S△ABC=7，得出S△PBC=13×7=73，设点P的坐标为(m,0)，得出12(1−m)=73，求出m的值，即可得出答案．
本题主要考查了平面直角坐标系中三角形的面积计算，解题的关键是作出辅助线，利用割补法求出△ABC的面积．
16.【答案】12
【解析】解：由题意可得：每一横行、每一竖列以及两条对角线上的3个数之和为x+20+6=26+x，
∴九宫格中左下角的数=(26+x)−(22+x)=4，
∴九宫格中间的数=(26+x)−(20+4)=2+x，
∴22+x+2+y=26+x，
解得：y=2，
由题意可得：x+x+2=20+y，
∴x=10，
∴x+y=12，
故答案为：12．
由每一横行、每一竖列以及两条对角线上的3个数之和相等可求九宫格中左下角的数和九宫格中间的数，列出方程可求x，y的值，即可求解．
本题考查了一元一次方程的应用，理解题意是解题的关键．
17.【答案】解：(1)原式=−9+5+1−(−2)
=−9+5+1+2
=−1；
(2)方程组整理得：3x−y=−1①3x+5y=11②，
②−①得：6y=12，
解得：y=2，
把y=2代入①得：3x−2=−1，
解得：x=13，
则原方程组的解为x=13y=2；
(3)13x−1≤3−53x①x−715解不等式①，得：x≤2，
解不等式②，得：x>−12，
∴不等式组的解集为−12解集表示在数轴上如下：

则其整数解是0、1、2．
【解析】(1)原式利用乘方的意义，算术平方根、立方根定义，以及绝对值的代数意义计算即可求出值；
(2)方程组整理后，利用加减消元法求出解即可；
(3)分别求出不等式组中两不等式的解集，找出两解集的公共部分确定出不等式组的解集，表示在数轴上，求出整数解即可．
此题考查了解一元一次不等式，解二元一次方程组，以及实数的运算，熟练掌握运算法则及各自的解法是解本题的关键．
18.【答案】30 0.3 0.4
【解析】解：(1)由题意得：a=150−15−45−60=30，b=45÷150=0.3，c=60÷150=0.4，
故答案为：30，0.3，0.4；
(2)补全频数分布直方图如下：

(3)360×0.4=144(名)，
答：估计在知识竞赛中取得90分以上的学生大约有144名．
(1)由抽取的人数减去其它三个组的频数得出a的值，再由频率的定义求出b、c即可；
(2)由(1)中a的值，补全频数分布直方图即可；
(3)用360乘样本中90分以上的学生的频率即可．
本题考查频数分布直方图、频数分布表、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．
19.【答案】BC 内错角相等，两直线平行 ∠5 ∠A 同位角相等，两直线平行 两直线平行，同旁内角互补 CF 同旁内角互补，两直线平行
【解析】解：∵∠3=∠4(已知)，
∴AE//BC(内错角相等，两直线平行)，
∴∠EDC=∠5(两直线平行，内错角相等)，
∵∠5=∠A(已知)，
∴∠EDC=∠A(等量代换)，
∴DC//AB(同位角相等，两直线平行)，
∴∠5+∠ABC=180°(两直线平行，同旁内角互补)，
即∠5+∠2+∠3=180°，
∵∠1=∠2(已知)，
∴∠5+∠1+∠3=180°(等量代换)，
即∠BCF+∠3=180°，
∴BE//CF(同旁内角互补，两直线平行)．
故答案为：BC；内错角相等，两直线平行；∠5；∠A；同位角相等，两直线平行；两直线平行，同旁内角互补；CF；同旁内角互补，两直线平行．
按照所给的证明思路，利用平行线的判定与性质定理，完善证明过程即可．
此题主要考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解答此题的关键．
20.【答案】(3,2) (1,−2) (a+c2,b+d2) (−1,2)
【解析】解：((1)如图，点A(1,2)，B(5,2)，C(−1,−1)，D(3,−3)在平面直角坐标系中描出它们如下：

线段AB和CD中点M、N的坐标分别为M(1+52,2+22)，N(−1+32,−1−32)，
故答案为：(3,2)，(1,−2)，
(2)①若线段的两个端点的坐标分别为(a,b)，(c,d)，则线段的中点坐标为(a+c2,b+d2)，
故答案为：(a+c2,b+d2)；
②∵P(−3,7)，Q(1,−3)，
∴由中点坐标公式得(−3+12,7−32)，即(−1,2)，
故答案为：(−1,2)．
(1)根据坐标的确定方法直接描点，分别读出各点的纵横坐标，即可得到各中点的坐标；
(2)①根据(1)中的坐标与中点坐标找到规律；
②利用①中的规律即可答题．
本题考查了坐标与图形性质，熟记平面直角坐标系中线段中点的横坐标为对应线段的两个端点的横坐标的平均数，中点的纵坐标为对应线段的两个端点的纵坐标的平均数是解题的关键．
21.【答案】解：(1)设l辆A型车载满货物一次可运货x吨，l辆B型车载满货物一次可运货y吨，
依题意得：3x+2y=172x+3y=18，
解得：x=3y=4．
答：l辆A型车载满货物一次可运货3吨，l辆B型车载满货物一次可运货4吨．
(2)依题意得：3a+4b=35，
∴b=35−3a4，
又∵a，b均为自然数，
∴a=1b=8或a=5b=5或a=9b=2，
∴共有3种租车方案，
方案1：租用A型车1辆，B型车8辆；
方案2：租用A型车5辆，B型车5辆；
方案3：租用A型车9辆，B型车2辆．
(3)选择方案1所需租车费为1×300+8×320=2860(元)；
选择方案2所需租车费为5×300+5×320=3100(元)；
选择方案3所需租车费为9×300+2×320=3340(元)．
∵2860<3100<3340，
∴最省钱的租车方案是方案1：租用A型车1辆，B型车8辆，最少租车费为2860元．
【解析】(1)设l辆A型车载满货物一次可运货x吨，l辆B型车载满货物一次可运货y吨，根据表格中的数据，即可得出关于x，y的二元一次方程组，解之即可得出结论；
(2)根据租用的车一次运完35吨货物且恰好每辆车都载满货物，即可得出关于a，b的二元一次方程，再结合a，b均为自然数，即可得出各租车方案；
(3)分别求出选择各方案所需租车费用，比较后即可得出结论．
本题考查了二元一次方程组的应用、二元一次方程的应用以及有理数的混合运算，找准等量关系，正确列出二元一次方程组(或二元一次方程)是解题的关键．
22.【答案】解：(1)∵ 3a−b−6+(a−b+2)2=0，
∴3a−b−6=0a−b+2=0，
解得a=4b=6，
∴点A(2,4)，B(6,2)；
(2)分别过点A，B作AC⊥x轴于C，BD⊥x轴于D，

∵点A(2,4)，B(6,2)；
∴AC=4，OC=2，OD=6，BD=2，CD=6−2=4，
∴S△AOB=S△AOC+S梯形ACDB−S△BOD=12×2×4+12(4+2)×4−12×6×2=4+12−6=10．
(3)①如图，作CM⊥x轴于M，CN⊥y轴于N，连接OC，

∵点A(2,4)，B(6,2)，
∴点E(0,2)，点F(4,0)，
即OE=2，OF=4，
∴S△EOF=12×4×2=4，
又∵S△EOF=S△EOC+S△COE，
∴4=12×2×m+12×4×n=m+2n，
∴m、n满足的关系式为：m+2n=4．
②∵点A(2,4)，B(6,2)，
∴点E(−4,0)，OE=4，
∵点D在直线EF上，且D点的纵坐标为t，
∴S△DOE=12×4×|t|=2|t|，
∵12S△DOE≥23S△AOB，
∴12×2|t|≥23×10，
∴|t|≥203，
解得t≤−203或t≥203，
∴当满足12S△DOE≥23S△AOB时，t的取值范围是t≤−203或t≥203．
【解析】(1)根据非负数的性质得，3a−b−6=0a−b+2=0，解方程即可；
(2)分别过点A，B作AC⊥x轴于C，BD⊥x轴于D，根据S△AOB=S△AOC+S梯形ACDB−S△BOD，代入计算即可；
(3)①作CM⊥x轴于M，CN⊥y轴于N，连接OC，由平移的性质得出点E、F的坐标，再根据S△EOF=S△EOC+S△COE，从而得出m和n的关系；
②由①同理可解决问题．
本题是三角形综合题，主要考查了非负数的性质，平移的性质，三角形的面积等知识，利用和差关系表示三角形的面积是解题的关键．
23.【答案】解：路径：方程的定义一方程的解一解方程—方程的应用；我们将来还可能研究一元
二次方程、一元三次方程、二元二次方程组等等(只要按照元和次数两方面作答均可以)．
如：一元三次方程x3+2x+1=0．
【解析】根据一元一次方程和二元一次方程组的定义得出答案即可．
本题考查了二元一次方程组，二元一次方程等知识点，能熟记一元一次方程，二元一次方程组的定义是解此题的关键，注意：①只含有一个未知数，并且所含未知数的最高次数是1的整式方程叫一元一次方程，②由几个二元一次方程组成，并且共含有两个不同的未知数，并且所含未知数的项的最高次数都是1，且每个方程都是整式方程，这样的方程组叫二元一次方程组．
4
9
2
3
5
7
8
1
6
x
6
20
22
y
成绩x/分
频数
频率
60≤x<70
15
0.1
70≤x<80
a
0.2
80≤x<90
60
b
90≤x<100
45
c
A型车(辆)
B型车(辆)
共运货(吨)
3
2
17
2
3
18