


2022-2023学年湖南省长沙市雨花区雅礼中学七年级数学第二学期期末达标检测模拟试题含答案
展开2022-2023学年湖南省长沙市雨花区雅礼中学七年级数学第二学期期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.如图,在四个均由十六个小正方形组成的正方形网格中,各有一个三角形ABC,那么这四个三角形中,不是直角三角形的是( )
A.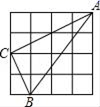 B.
B.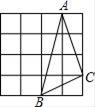
C.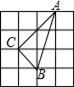 D.
D.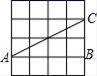
2.由下列条件不能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C B.∠A:∠B:∠C=1:3:2
C.a=2,b=3,c=4 D.(b+c)(b-c)=a²
3.有19位同学参加歌咏比赛,所得的分数互不相同,取得分前10位的同学进入决赛,某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学分数的( )
A.平均数 B.中位数 C.众数 D.方差
4.下列事件中,属于随机事件的是( )
A.抛出的篮球往下落 B.在只有白球的袋子里摸出一个红球
C.购买![]() 张彩票,中一等奖 D.地球绕太阳公转
张彩票,中一等奖 D.地球绕太阳公转
5.a,b,c为常数,且![]() ,则关于x的方程
,则关于x的方程![]() 根的情况是
根的情况是![]()
![]()
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.有一根为0
6.下列图形中,既是轴对称又是中心对称图形的是( )
A.菱形 B.等边三角形 C.平行四边形 D.直角三角形
7.某校艺术节的乒乓球比赛中,小东同学顺利进入决赛.有同学预测“小东夺冠的可能性是80%”,则对该同学的说法理解最合理的是( )
A.小东夺冠的可能性较大 B.如果小东和他的对手比赛10局,他一定会赢8局
C.小东夺冠的可能性较小 D.小东肯定会赢
8.如图,在△ABC中,D,E,F分别是AB,BC,AC边的中点.如果添加一个条件,使四边形ADEF是菱形,则添加的条件为( )
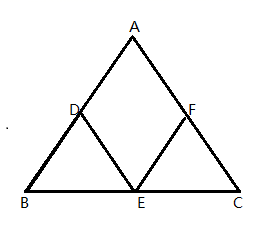
A.AB=AC B.AC=BC C.∠A=90° D.∠A=60°
9.如图,正方形网格中的每个小正方形的边长为1,将![]() 绕旋转中心旋转某个角度后得到
绕旋转中心旋转某个角度后得到![]() ,其中点A,B,C的对应点是点
,其中点A,B,C的对应点是点![]() ,
,![]() ,
,![]() ,那么旋转中心是( )
,那么旋转中心是( )
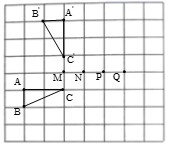
A.点Q B.点P C.点N D.点M
10.有一组数据7、11、12、7、7、8、11,下列说法错误的是( )
A.中位数是7 B.平均数是9 C.众数是7 D.极差为5
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .
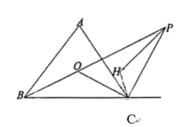
12.已知在△ABC中,∠ABC和∠ACB的角平分线交于O,且∠ABC的角平分线与∠ACB的外角平分线交于P,∠OPC和∠OCP角平分线交于H,∠H=117.5°,则∠A=________
13.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,将
,将![]() 绕点
绕点![]() 旋转至
旋转至![]() ,连接
,连接![]() ,
,![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 的最大值为_________.
的最大值为_________.
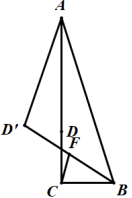
14.已知线段a,b,c能组成直角三角形,若a=3,b=4,则c=_____.
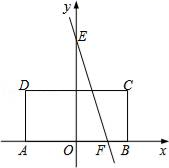
15.如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2, AD=1,点E的坐标为(0,2).点F(x,0)在边AB上运动,若过点E、F的直线将矩形ABCD的周长分成2:1两部分,则x的值为__.
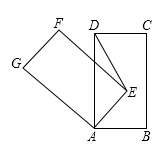
16.如图,将一个![]() 智屏手机抽象成一个的矩形
智屏手机抽象成一个的矩形![]() ,其中
,其中![]() ,
,![]() ,然后将它围绕顶点
,然后将它围绕顶点![]() 逆时针旋转一周,旋转过程中
逆时针旋转一周,旋转过程中![]() 、
、![]() 、
、![]() 、
、![]() 的对应点依次为
的对应点依次为![]() 、
、![]() 、
、![]() 、
、![]() ,则当
,则当![]() 为直角三角形时,若旋转角为
为直角三角形时,若旋转角为![]() ,则
,则![]() 的大小为______.
的大小为______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)人教版八年级下册第19章《一次函数》中“思考”:这两个函数的图象形状都是直线,并且倾斜程度相同,函数![]() 的图象经过原点,函数
的图象经过原点,函数![]() 的图象经与y轴交于点(0,5),即它可以看作直线
的图象经与y轴交于点(0,5),即它可以看作直线![]() 向上平移5个单位长度而得到。比较一次函数解析式
向上平移5个单位长度而得到。比较一次函数解析式![]() 与正比例函数解析式
与正比例函数解析式![]() ,容易得出:一次函数
,容易得出:一次函数![]() 的图象可由直线
的图象可由直线![]() 通过向上(或向下)平移
通过向上(或向下)平移![]() 个单位得到(当b>0时,向上平移,当b<0时,向下平移)。
个单位得到(当b>0时,向上平移,当b<0时,向下平移)。
(结论应用)一次函数![]() 的图象可以看作正比例函数 的图象向 平移 个单位长度得到;
的图象可以看作正比例函数 的图象向 平移 个单位长度得到;
(类比思考)如果将直线![]() 的图象向右平移5个单位长度,那么得到的直线的函数解析式是怎样的呢?我们可以这样思考:在直线
的图象向右平移5个单位长度,那么得到的直线的函数解析式是怎样的呢?我们可以这样思考:在直线![]() 上任意取两点A(0,0)和B(1,
上任意取两点A(0,0)和B(1,![]() ),将点A(0,0)和B(1,
),将点A(0,0)和B(1,![]() )向右平移5个单位得到点C(5,0)和D(6,
)向右平移5个单位得到点C(5,0)和D(6,![]() ),连接CD,则直线CD就是直线AB向右平移5个单位长度后得到的直线,设直线CD的解析式为:
),连接CD,则直线CD就是直线AB向右平移5个单位长度后得到的直线,设直线CD的解析式为:![]() ,将C(5,0)和D(6,
,将C(5,0)和D(6,![]() )代入得到:
)代入得到:![]() 解得
解得![]() ,所以直线CD的解析式为:
,所以直线CD的解析式为:![]() ;①将直线
;①将直线![]() 向左平移5个单位长度,则平移后得到的直线解析式为 .②若先将直线
向左平移5个单位长度,则平移后得到的直线解析式为 .②若先将直线![]() 向左平移4个单位长度后,再向上平移5个单位长度,得到直线
向左平移4个单位长度后,再向上平移5个单位长度,得到直线![]() ,则直线
,则直线![]() 的解析式为: .
的解析式为: .
(拓展应用)已知直线![]() :
:![]() 与直线关于x轴对称,求直线的解析式.
与直线关于x轴对称,求直线的解析式.
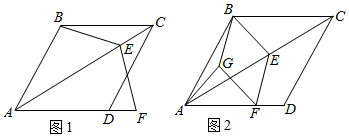
18.(8分)如图,在菱形ABCD中,∠ABC=120°,AB=4![]() ,E为对角线AC上的动点(点E不与A,C重合),连接BE,将射线EB绕点E逆时针旋转120°后交射线AD于点F.
,E为对角线AC上的动点(点E不与A,C重合),连接BE,将射线EB绕点E逆时针旋转120°后交射线AD于点F.
(1)如图1,当AE=AF时,求∠AEB的度数;
(2)如图2,分别过点B,F作EF,BE的平行线,且两直线相交于点G.
①试探究四边形BGFE的形状,并求出四边形BGFE的周长的最小值;
②连接AG,设CE=x,AG=y,请直接写出y与x之间满足的关系式,不必写出求解过程.
19.(8分)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() ,
,![]() 上,连接
上,连接![]() .
.
(1)将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,如图1,若
处,如图1,若![]() ,求
,求![]() 的长;
的长;
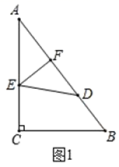
(2)将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,如图2,若
处,如图2,若![]() .
.
①求![]() 的长;
的长;
②求四边形![]() 的面积;
的面积;
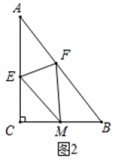
(3)若点![]() 在射线
在射线![]() 上,点
上,点![]() 在边
在边![]() 上,点
上,点![]() 关于
关于![]() 所在直线的对称点为点
所在直线的对称点为点![]() ,问:是否存在以
,问:是否存在以![]() 、
、![]() 为对边的平行四边形,若存在,求出
为对边的平行四边形,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
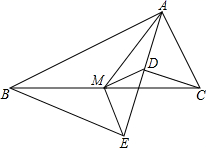
20.(8分)如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
(1)若AB=8,AC=4,求DE的长;
(2)求证:AB-AC=2DM.
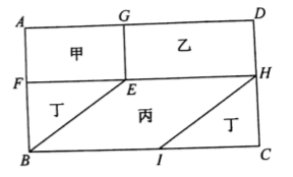
21.(8分)市政规划出一块矩形土地用于某项目开发,其中![]()
![]() ,设计分区如图所示,
,设计分区如图所示,![]() 为矩形内一点,作
为矩形内一点,作![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,
,![]() 过点
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,其中丙区域用于主建筑区,其余各区域均用于不同种类绿化.
,其中丙区域用于主建筑区,其余各区域均用于不同种类绿化.
![]() 若点
若点![]() 是
是![]() 的中点,求
的中点,求![]() 的长;
的长;
![]() 要求绿化占地面积不小于
要求绿化占地面积不小于![]() ,规定乙区域面积为
,规定乙区域面积为![]()
①若将甲区域设计成正方形形状,能否达到设计绿化要求?请说明理由;
②若主建筑丙区域不低于乙区域面积的![]() ,则
,则![]() 的最大值为
的最大值为 ![]() (请直接写出答案)
(请直接写出答案)
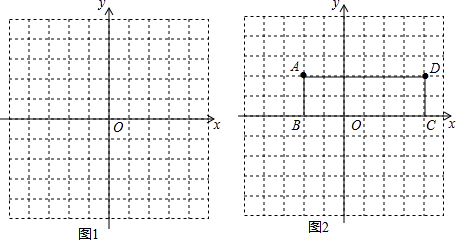
22.(10分)已知直线y=kx+3(1-k)(其中k为常数,k≠0),k取不同数值时,可得不同直线,请探究这些直线的共同特征.
实践操作
(1)当k=1时,直线l1的解析式为 ,请在图1中画出图象;当k=2时,直线l2的解析式为 ,请在图2中画出图象;
探索发现
(2)直线y=kx+3(1-k)必经过点( , );
类比迁移
(3)矩形ABCD如图2所示,若直线y=kx+k-2(k≠0)分矩形ABCD的面积为相等的两部分,请在图中直接画出这条直线.
23.(10分)解方程:2x2﹣4x+1=0.(用配方法)
24.(12分)小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:
(1)小帅的骑车速度为 千米/小时;点C的坐标为 ;
(2)求线段AB对应的函数表达式;
(3)当小帅到达乙地时,小泽距乙地还有多远?
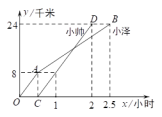
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、B
4、C
5、B
6、A
7、A
8、A
9、C
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1。
12、70°
13、![]() +2
+2
14、5或![]()
15、![]() 或﹣
或﹣![]() .
.
16、![]() 或
或![]() 或
或![]()
三、解下列各题(本大题共8小题,共72分)
17、
18、(1)45°;(2)①四边形BEFG是菱形,8![]() ;② y=
;② y=![]() (0<x<12)
(0<x<12)
19、 (1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)存在,
;(3)存在,![]() 或6.
或6.
20、(1)![]() ;(2)证明见解析.
;(2)证明见解析.
21、(1)90m;(2)①能达到设计绿化要求,理由见解析,②40
22、(1)y=x,见解析;y=2x-3,见解析;(2)(3,3);(3)见解析.
23、x1=1+![]() ,x2=1﹣
,x2=1﹣![]() .
.
24、 (1)16,C(0.5,0);(2)![]() ;(3)4千米.
;(3)4千米.
湖南省长沙市雨花区雅礼中学2023-2024学年九年级数学第一学期期末达标检测试题含答案: 这是一份湖南省长沙市雨花区雅礼中学2023-2024学年九年级数学第一学期期末达标检测试题含答案,共8页。试卷主要包含了的值为,已知抛物线y=x2+,若y=是二次函数,则m等于等内容,欢迎下载使用。
湖南省长沙市雨花区雅礼中学2023-2024学年数学八上期末复习检测试题含答案: 这是一份湖南省长沙市雨花区雅礼中学2023-2024学年数学八上期末复习检测试题含答案,共7页。试卷主要包含了如图,,于,于,,则的值为,如图,点A的坐标为等内容,欢迎下载使用。
2023-2024学年湖南长沙市雅礼洋湖实验中学八上数学期末达标检测模拟试题含答案: 这是一份2023-2024学年湖南长沙市雅礼洋湖实验中学八上数学期末达标检测模拟试题含答案,共7页。试卷主要包含了下列命题是假命题的是,二元一次方程组的解是等内容,欢迎下载使用。












