


2022-2023学年江苏省苏州昆山市、太仓市数学七年级第二学期期末学业水平测试试题含答案
展开2022-2023学年江苏省苏州昆山市、太仓市数学七年级第二学期期末学业水平测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.用配方法解方程![]() 时,配方后正确的是( )
时,配方后正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
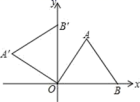
2.如图,△AOB是等边三角形,B(2,0),将△AOB绕O点逆时针方向旋转90°到△A′OB′位置,则A′坐标是( )
A.(﹣1,![]() ) B.(﹣
) B.(﹣![]() ,1) C.(
,1) C.(![]() ,﹣1) D.(1,﹣
,﹣1) D.(1,﹣![]() )
)
3. “凤鸣”文学社在学校举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,某组共互赠了210本图书,如果设该组共有x名同学,那么依题意,可列出的方程是( )
A.x(x+1)=210 B.x(x﹣1)=210
C.2x(x﹣1)=210 D.![]() x(x﹣1)=210
x(x﹣1)=210
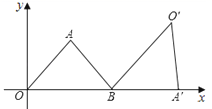
4.如图,△AOB为等腰三角形,顶点A的坐标(2,![]() ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A.(![]() ,
,![]() ) B.(
) B.(![]() ,
,![]() ) C.(
) C.(![]() ,
,![]() ) D.(
) D.(![]() ,4
,4![]() )
)
5.函数![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x>1 B.x<1 C.![]() D.
D.![]()
6.如图,函数y=![]() 与y=﹣kx+1(k≠0)在同一直角坐标系中的图象大致为( )
与y=﹣kx+1(k≠0)在同一直角坐标系中的图象大致为( )
A.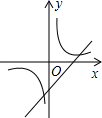 B.
B.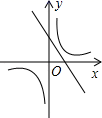
C.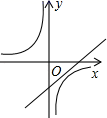 D.
D.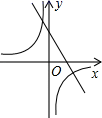
7.如图所示,正方形ABCD的边长为6,M在DC上,且DM=4,N是AC上的动点,则DN+MN的最小值是( )
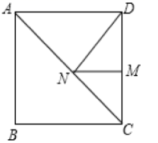
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,将点P(-2,3)向右平移n个单位后落在直线y=2x-1上的点P'处,则n等于( )
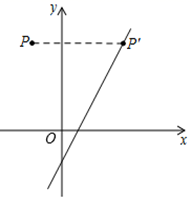
A.4 B.5 C.6 D.7
9.如图这个几何体的左视图正确的是( )
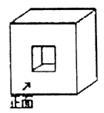
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知三角形两边长为2和6,要使该三角形为直角三角形,则第三边的长为( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.以上都不对
D.以上都不对
二、填空题(本大题共有6小题,每小题3分,共18分)
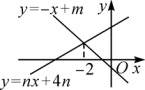
11.如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+4n的解集为____________.
12.已知一个样本的数据为1、2、3、4、x,它的平均数是3,则这个样本方差![]() =_______
=_______
13.已知m是方程x2﹣2018x+1=0的一个根,则代数式m2﹣2017m+![]() +3的值等于_____.
+3的值等于_____.
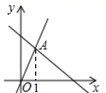
14.如图,函数![]() (
(![]() )和
)和![]() (
(![]() )的图象相交于点
)的图象相交于点![]() ,则不等式
,则不等式![]() 的解集为_________.
的解集为_________.
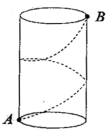
15.如图,圆柱体的高为8cm,底面周长为4cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图所示,则最短路程为_____.
16.用配方法解一元二次方程x2-mx=1时,可将原方程配方成(x-3)2=n,则m+n的值是 ________ .
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,D为AB上一点,△ACE≌△BCD,AD2+DB2=DE2,试判断△ABC的形状,并说明理由.
18.(8分)学校组织八年级350名学生参加“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
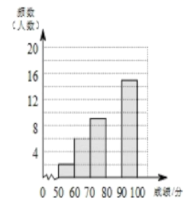
请根据所给信息,解答下列问题:
(1)求a和b的值;
(2)请补全频数分布直方图。
19.(8分)已知正方形![]() 与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
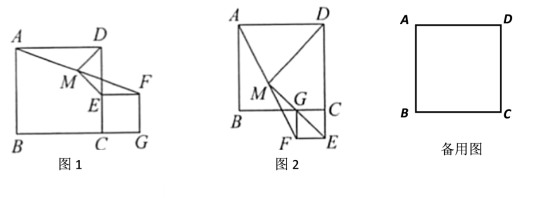
(1)如图1,点![]() 在上,点在的延长线上,
在上,点在的延长线上,
求证:![]() =ME,
=ME,![]() ⊥.ME
⊥.ME
简析: 由是的中点,AD∥EF,不妨延长EM交AD于点N,从而构造出一对全等的三角形,即 ≌ .由全等三角形性质,易证△DNE是 三角形,进而得出结论.
(2)如图2, 在![]() 的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
(3)当AB=5,CE=3时,正方形的顶点C、E、F、G按顺时针排列.若点![]() 在直线CD上,则DM= ;若点E在直线BC上,则DM= .
在直线CD上,则DM= ;若点E在直线BC上,则DM= .
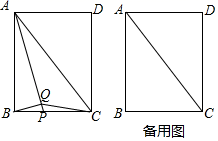
20.(8分)如图,在矩形![]() 中,
中,![]() 为对角线,点
为对角线,点![]() 为
为![]() 边上一动点,连结
边上一动点,连结![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
(1)证明:![]() ;
;
(2)当点![]() 为
为![]() 的中点时,若
的中点时,若![]() ,求
,求![]() 的度数;
的度数;
(3)当点![]() 运动到与点
运动到与点![]() 重合时,延长
重合时,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() .
.
21.(8分)新定义:[a,b,c]为二次函数y=ax2+bx+e(a≠0,a,b,c为实数)的“图象数”,如:y=-x2+2x+3的“图象数”为[-1,2,3]
(1)二次函数y=![]() x2-x-1的“图象数”为 .
x2-x-1的“图象数”为 .
(2)若图象数”是[m,m+1,m+1]的二次函数的图象与x轴只有一个交点,求m的值.
22.(10分)解分式方程:![]() =
=![]()
23.(10分)如图1,已知直线![]() :
:![]() 交
交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() .
.
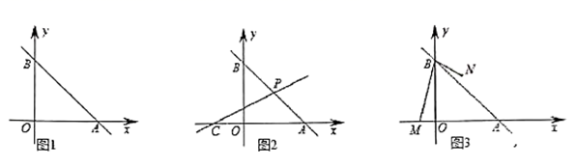
(1)直接写出![]() 的值为______.
的值为______.
(2)如图2,![]() 为
为![]() 轴负半轴上一点,过
轴负半轴上一点,过![]() 点的直线
点的直线![]() :
:![]() 经过
经过![]() 的中点
的中点![]() ,点
,点![]() 为
为![]() 轴上一动点,过
轴上一动点,过![]() 作
作![]() 轴分别交直线
轴分别交直线![]() 、
、![]() 于
于![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(3)如图3,已知点![]() ,点
,点![]() 为直线
为直线![]() 右侧一点,且满足
右侧一点,且满足![]() ,求点
,求点![]() 坐标.
坐标.
24.(12分)关于x的方程:![]() -
-![]() =1.
=1.
(1)当a=3时,求这个方程的解;
(2)若这个方程有增根,求a的值.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、B
4、C
5、C
6、B
7、B
8、A
9、C
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]() <-1
<-1
12、2
13、1
14、![]()
15、10cm
16、16
三、解下列各题(本大题共8小题,共72分)
17、△ABC是等腰直角三角形,理由见解析.
18、(1)18,0.18;(2)见解析
19、(1)等腰直角;(2)结论仍成立,见解析;(3)![]() 或
或![]() ,
,![]() .
.
20、(1)见解析;(2)53°;(3) ![]()
21、(1)[![]() ,−1,−1];(2)m1=−1,m2=
,−1,−1];(2)m1=−1,m2=![]() .
.
22、x=1
23、(1)k=-1;(2)![]() 或
或![]() ;(3)
;(3)![]()
24、(1)x=-2;(2)a=-3.
江苏省苏州市昆山市、太仓市2023-2024学年数学九上期末联考模拟试题含答案: 这是一份江苏省苏州市昆山市、太仓市2023-2024学年数学九上期末联考模拟试题含答案,共7页。试卷主要包含了方程x2=3x的解为,一元二次方程的根的情况是等内容,欢迎下载使用。
江苏省苏州昆山市、太仓市2023-2024学年数学九年级第一学期期末综合测试模拟试题含答案: 这是一份江苏省苏州昆山市、太仓市2023-2024学年数学九年级第一学期期末综合测试模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,抛物线y=的对称轴方程为等内容,欢迎下载使用。
江苏省昆山市、太仓市2023-2024学年九上数学期末预测试题含答案: 这是一份江苏省昆山市、太仓市2023-2024学年九上数学期末预测试题含答案,共7页。试卷主要包含了如图,点,已知抛物线具有如下性质,抛物线的顶点坐标是等内容,欢迎下载使用。












