


2022-2023学年湖南省湘潭市数学七下期末质量检测模拟试题含答案
展开2022-2023学年湖南省湘潭市数学七下期末质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.![]() 等于( )
等于( )
A.2 B.0 C.![]() D.-2019
D.-2019
2.已知一组数据1,l,![]() ,7,3,5,3,1的众数是1,则这组数据的中位数是( ).
,7,3,5,3,1的众数是1,则这组数据的中位数是( ).
A.1 B.1.5 C.3 D.5
3.为了保障艺术节表演的整体效果,某校在操场中标记了几个关键位置,如图是利用平面直角坐标系画出的关键位置分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示点A的坐标为![]() ,表示点B的坐标为
,表示点B的坐标为![]() ,则表示其他位置的点的坐标正确的是( )
,则表示其他位置的点的坐标正确的是( )
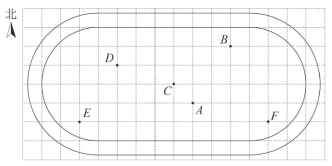
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列4个命题:
①对角线相等且互相平分的四边形是正方形;
②有三个角是直角的四边形是矩形;
③对角线互相垂直的平行四边形是菱形;
④一组对边平行,另一组对边相等的四边形是平行四边形
其中正确的是( )
A.②③ B.② C.①②④ D.③④
5.将点A(-2,-3)向左平移3个单位,再向上平移2个单位得到点B,则B的坐标是( )
A.(1,-3) B.(-2,1) C.(-5,-1) D.(-5,-5)
6.一次函数y=kx+b,当k<0,b<0时,它的图象大致为( )
A.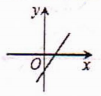 B.
B.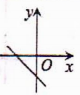 C.
C.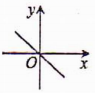 D.
D.
7.将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A.y=﹣3x+2 B.y=﹣3x﹣2 C.y=﹣3(x+2) D.y=﹣3(x﹣2)
8.关于x的一元二次方程![]() 的两实数根分别为
的两实数根分别为![]() 、
、![]() ,且
,且![]() ,则m的值为( )
,则m的值为( )
A.![]() B.
B.![]() C.
C.![]() D.0
D.0
9.正方形具有而菱形不具有的性质是( )
A.对角线平分一组对角 B.对角互补
C.四边相等 D.对边平行
10.如图,![]()
![]() 的对角线AC,BD相交于点O,
的对角线AC,BD相交于点O,![]() 是AB中点,且AE+EO=4,则
是AB中点,且AE+EO=4,则![]() 的周长为
的周长为![]()
![]()
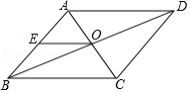
A.20 B.16 C.12 D.8
二、填空题(本大题共有6小题,每小题3分,共18分)
11.如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是_________.

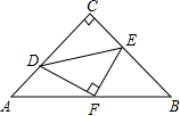
12.如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE;②四边形CDFE不可能是正方形;③△DFE是等腰直角三角形;④S四边形CDFE=![]() S△ABC.上述结论中始终正确的有______.(填序号)
S△ABC.上述结论中始终正确的有______.(填序号)
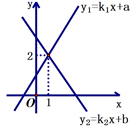
13.如图,直线![]() 与
与![]() 的交点坐标为
的交点坐标为![]() ,当
,当![]() 时,则
时,则![]() 的取值范围是__________.
的取值范围是__________.
14.已知点(2,7)在函数y=ax+3的图象上,则a的值为____.
15.如图,在矩形ABCD中,AD=10,AB=8,点P在AD上,且BP=BC,点M在线段BP上,点N在线段BC的延长线上,且MP=NC,连接MN交线段PC于点F,过点M作ME⊥PC于点E,则EF= _______.

16.为方便市民出行,2019年北京地铁推出了电子定期票,电子定期票在使用有效期限内,支持单人不限次数乘坐北京轨道交通全路网(不含机场线)所有线路,电子定期票包括一日票、二日票、三日票、五日票及七日票共五个种类,价格如下表:
种类 | 一日票 | 二日票 | 三日票 | 五日票 | 七日票 |
单价(元/张) | 20 | 30 | 40 | 70 | 90 |
某人需要连续6天不限次数乘坐地铁,若决定购买电子定期票,则总费用最低为____元.
三、解下列各题(本大题共8小题,共72分)
17.(8分)为了从甲、乙两名学生中选拨一人参加射击比赛,对他们的射击水平进行了测验,两人在相同条件下各射靶6次,命中的环数如下:
甲:7,8,6,10,10,7
乙:7, 7,8,8,10,8,
如果你是教练你会选拨谁参加比赛?为什么?
18.(8分)已知等腰三角形的周长为![]() , 底边长
, 底边长![]() 是腰长
是腰长![]() 的函数.
的函数.
![]() 写出这个函数关系式;
写出这个函数关系式;
![]() 求自变量
求自变量![]() 的取值范围;
的取值范围;
![]() 画出这个函数的图象.
画出这个函数的图象.
19.(8分)如图,E、F是平行四边形ABCD的对角线AC上的点,且CE=AF.
求证:BE∥DF.
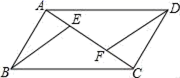
20.(8分)已知![]() (如图),点
(如图),点![]() 分别在边
分别在边![]() 上,且四边形
上,且四边形![]() 是菱形
是菱形
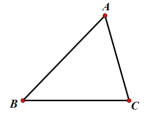
(1)请使用直尺与圆规,分别确定点![]() 的具体位置(不写作法,保留画图痕迹);
的具体位置(不写作法,保留画图痕迹);
(2)如果![]() ,点
,点![]() 在边
在边![]() 上,且满足
上,且满足![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)当![]() 时,求
时,求![]() 的值。
的值。
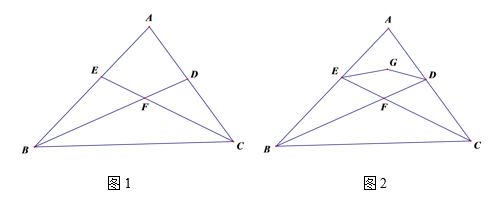
21.(8分)如图1,在![]() ABC中,∠A=80°,BD、CE分别平分∠ABC、∠ACB,BD与CE交于点F.
ABC中,∠A=80°,BD、CE分别平分∠ABC、∠ACB,BD与CE交于点F.
(1)求∠BFC的度数;
(2)如图2,EG、DG分别平分∠AEF、∠ADF, EG与DG交于点G ,求∠EGD的度数.
22.(10分)定义:对于给定的一次函数y=ax+b(a≠0),把形如![]() 的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
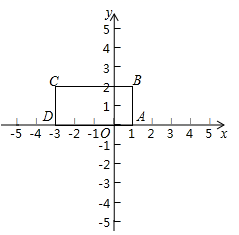
(1)已知函数y=2x+l.
①若点P(-1,m)在这个一次函数的衍生函数图像上,则m= .
②这个一次函数的衍生函数图像与矩形ABCD的边的交点坐标分别为 .
(2)当函数y=kx-3(k>0)的衍生函数的图象与矩形ABCD有2个交点时,k的取值范围是 .
23.(10分)一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.
,那么称这个四位数为“和平数”.
例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(2)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后的这两个“和平数”为一组“相关和平数”.
例如:1423与4132为一组“相关和平数”
求证:任意的一组“相关和平数”之和是1111的倍数.
(3)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”;
24.(12分)某商店计划购进甲、乙两种商品,乙种商品的进价是甲种商品进价的九折,用3600元购买乙种商品要比购买甲种商品多买10件.
(1)求甲、乙两种商品的进价各是多少元?
(2)该商店计划购进甲、乙两种商品共80件,且乙种商品的数量不低于甲种商品数量的3倍.甲种商品的售价定为每件80元,乙种商品的售价定为每件70元,若甲、乙两种商品都能卖完,求该商店能获得的最大利润.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、B
3、B
4、A
5、C
6、B
7、A
8、A
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、①③④
13、![]()
14、1.
15、![]()
16、1
三、解下列各题(本大题共8小题,共72分)
17、应选乙参加比赛.
18、(1)![]() ;(2)
;(2)![]() ;(3)见详解.
;(3)见详解.
19、证明见解析.
20、(1)详见解析;(2)![]() ;(3)
;(3)![]()
21、(1)130〬(2)155〬
22、(1)①1,②(![]() ,2)或(
,2)或(![]() ,,0);(2)1<k<1;
,,0);(2)1<k<1;
23、(1)1001,9999;(2)见详解;(3)2754和1
24、(1)甲、乙两种商品的进价各是40元/件、36元/件;(2)该商店获得的最大利润是2840元.
湖南省张家界市名校2022-2023学年七下数学期末教学质量检测模拟试题含答案: 这是一份湖南省张家界市名校2022-2023学年七下数学期末教学质量检测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列分式是最简分式的是,下列各点在反比例函数图象上的是等内容,欢迎下载使用。
湖南省澧县张公庙中学2022-2023学年数学七下期末教学质量检测模拟试题含答案: 这是一份湖南省澧县张公庙中学2022-2023学年数学七下期末教学质量检测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,在平面直角坐标系中,点P等内容,欢迎下载使用。
2022-2023学年湖南省邵阳市绥宁县七下数学期末质量检测模拟试题含答案: 这是一份2022-2023学年湖南省邵阳市绥宁县七下数学期末质量检测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下面是某八年级,若点,若分式的值为0,则的取值为,不等式组的解集是,下列各式中计算正确的是等内容,欢迎下载使用。












