2022-2023学年湖南省澧县七年级数学第二学期期末教学质量检测模拟试题含答案

2022-2023学年湖南省澧县七年级数学第二学期期末教学质量检测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．如图，直线经过点A(a，)和点B(，0)，直线经过点A，则当时，x的取值范围是（    ）

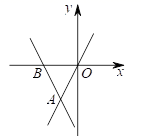
A．x>-1 B．x<-1 C．x>-2 D．x<-2

2．用配方法解方程时，原方程应变形为（  ）

A． B． C． D．

3．下列各组数据中，不能作为直角三角形边长的是（  ）

A． B． C． D．

4．对于函数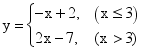下列说法正确的是　　

A．当时，y随x的增大而增大 B．当时，y随x的增大而减小

C．当时，y随x的增大而减小 D．当时，

5．某地开挖一条480米的渠道，开工后，实际每天比原计划多挖20米，结果提前4天完成任务，若设原计划每天挖米，那么所列方程正确的是(　　)

A． B．

C． D．

6．点到轴的距离为（    ）

A．3 B．4 C．5 D．

7．计算（）3÷的结果是（　　）

A． B．y2 C．y4 D．x2y2

8．平面直角坐标系中，点A的坐标为，将线段OA绕原点O逆时针旋转得到，则点的坐标是　　

A． B． C． D．

9．若关于x的不等式组的解集为x＜3，则k的取值范围为（　　）

A．k＞1 B．k＜1 C．k≥1 D．k≤1

10．已知空气的单位质量是0.001239g/cm3，用科学记数法表示该数为（   ）

A． B． C． D．

11．函数中，自变量x的取值范围是（ ）

A．x＞1 B．x＜1 C． D．

12．下列由线段、、组成的三角形中，不是直角三角形的为（   ）

A．，， B．，，

C．，， D．，，

二、填空题（每题4分，满分20分，将答案填在答题纸上）

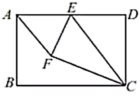
13．如图，矩形中，，，是边上一点，连接，将沿翻折，点的对应点是，连接，当是直角三角形时，则的值是________

14．已知点和都在第三象限的角平分线上，则_______．

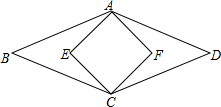
15．如图，B、E、F、D四点在同一条直线上，菱形ABCD的面积为120cm2，正方形AECF的面积为50cm2，则菱形的边长为_____cm．

16．化简：＝__________．

17．如图，已知，，，当时，______.

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）为保护环境，我市公交公司计划购买A型和B型两种环保节能公交车共10辆．若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．

（1）求购买A型和B型公交车每辆各需多少万元？

（2）预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？

（3）在（2）的条件下，哪种购车方案总费用最少？最少总费用是多少万元？

19．（5分）如图所示，矩形OABC的邻边OA、OC分别与x、y轴重合，矩形OABC的对称中心P(4，3)，点Q由O向A以每秒1个单位速度运动，点M由C向B以每秒2个单位速度运动，点N由B向C以每秒2个单位速度运动，设运动时间为t秒，三点同时出发，当一点到达终点时同时停止.

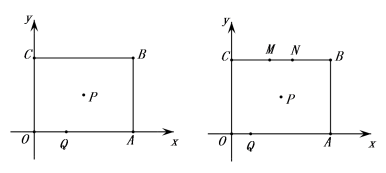
（1）根据题意，可得点B坐标为__________，AC＝_________；

（2）求点Q运动几秒时，△PCQ周长最小?

（3）在点M、N、Q的运动过程中，能否使以点O、Q、M、N为顶点的四边形是平行四边形？若能，请求出t值；若不能，请说明理由．

20．（8分）已知关于x的一元二次方程x2﹣2tx+t2﹣2t+4＝1．

（1）当t＝3时，解这个方程；

（2）若m，n是方程的两个实数根，设Q＝（m﹣2）（n﹣2），试求Q的最小值．

21．（10分）在综合与实践课上，老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.

（1）奋进小组用图1中的矩形纸片ABCD，按照如图2所示的方式，将矩形纸片沿对角线AC折叠，使点B落在点处，则与重合部分的三角形的类型是________.

（2）勤学小组将图2中的纸片展平，再次折叠，如图3，使点A与点C重合，折痕为EF，然后展平，则以点A、F、C、E为顶点的四边形是什么特殊四边形？请说明理由．

（3）创新小组用图4中的矩形纸片ABCD进行操作，其中，，先沿对角线BD对折，点C落在点的位置，交AD于点G，再按照如图5所示的方式折叠一次，使点D与点A重合，得折痕EN，EN交AD于点M．则EM的长为________cm.

22．（10分）在正方形ABCD中，P是对角线AC上的点，连接BP、DP.

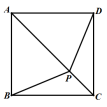
⑴求证：BP=DP；

⑵如果AB=AP，求∠ABP的度数.

23．（12分）若抛物线上，它与轴交于，与轴交于、，是抛物线上、之间的一点，

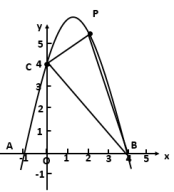
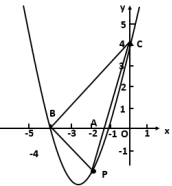
（1）当时，求抛物线的方程，并求出当面积最大时的的横坐标．

（2）当时，求抛物线的方程及的坐标，并求当面积最大时的横坐标．

（3）根据（1）、（2）推断的横坐标与的横坐标有何关系？

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、A

2、A

3、C

4、C

5、C

6、A

7、B

8、A

9、C

10、C

11、C

12、D

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、3或1

14、-6

15、1．

16、2x

17、1或

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）购买A型公交车每辆需100万元，购买B型公交车每辆需150万元．

（2）三种方案：①购买A型公交车6辆，则B型公交车4辆；②购买A型公交车7辆，则B型公交车3辆；③购买A型公交车8辆，则B型公交车2辆；

（3）购买A型公交车8辆，B型公交车2辆费用最少，最少费用为1100万元．

19、（1）10  （2）  （3）或

20、（2）x2＝3﹣，x2＝3+；（2）Q的最小值是﹣2．

21、（1）等腰三角形（或钝角三角形）；（2）菱形，理由详见解析；（3）.

22、 (1)证明见解析；（2）67.5°．

23、（1）2；（2）－2；（3）的横坐标等于的横坐标的一半