2022-2023学年湖南省常德芷兰实验学校七年级数学第二学期期末教学质量检测模拟试题含答案

这是一份2022-2023学年湖南省常德芷兰实验学校七年级数学第二学期期末教学质量检测模拟试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，设表示两个数中的最大值，例如等内容，欢迎下载使用。
2022-2023学年湖南省常德芷兰实验学校七年级数学第二学期期末教学质量检测模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．如图，在中，，，垂足为，点是边的中点，，，则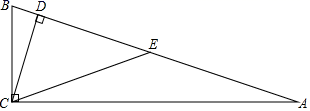（　　）A．8 B．7.5 C．7 D．62．下列命题是真命题的是（    ）A．对角线互相垂直且相等的四边形是正方形B．对角线相互平分的四边形是菱形C．对角线相互垂直的四边形是平行四边形D．对角线相等的平行四边形是矩形3．体育课上，某班三名同学分别进行了6次短跑训练，要判断哪一名同学的短跑成绩比较稳定，通常需要比较三名同学短跑成绩的 （    ）A．平均数 B．频数 C．方差 D．中位数4．如图，平行四边形ABCD中，M是BC的中点，且AM=9，BD=12，AD=10，则ABCD的面积是（　　）
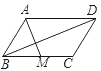 A．30 B．36 C．54 D．725．用反证法证明“三角形中至少有一个内角大于或等于60°”时，应先假设（　　）A．有一个内角小于60° B．每一个内角都小于60°C．有一个内角大于60° D．每一个内角都大于60°6．刘翔在出征北京奥运会前刻苦进行110米跨栏训练，教练对他20次的训练成绩进行统计分析，判断他的成绩是否稳定，则教练需要知道刘翔这20次成绩的（　　）A．众数 B．平均数 C．频数 D．方差7．如图，在平面直角坐标系中，菱形ABCD的顶点A在y轴上，已知B(﹣3，0)、C(2，0)，则点D的坐标为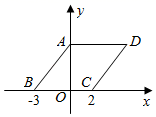（    ）A．(4，5) B．(5，4) C．(5，3) D．(4，3)8．设表示两个数中的最大值，例如：，，则关于的函数可表示为（  ）A． B． C． D．9．若从边形的一个顶点出发，最多可以作3条对角线，则该边形的内角和是（    ）A． B． C． D．10．如图，在矩形ABCD中，E，F，G，H分别为边AB，DA，CD，BC的中点．若AB＝2，AD＝4，则图中阴影部分的面积为(　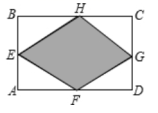　)A．3 B．4 C．6 D．811．若直线y=－2x－4与直线y=4x＋b的交点在第三象限，则b的取值范围是（    ）A．－4<b<8 B．－4<b<0 C．b<－4或b>8 D．－4≤6≤812．如图，菱形ABCD的对角线AC，BD相交于点O，E，F分别是AB，BC边上的中点，连接EF.若，BD=4，则菱形ABCD的周长为（    ）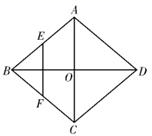A．4 B． C． D．28二、填空题（每题4分，满分20分，将答案填在答题纸上）13．如图所示，工人师傅做一个矩形铝合金窗框分下面三个步骤进行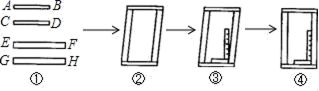先截出两对符合规格的铝合金窗料（如图①所示），使AB＝CD，EF＝GH．（1）摆放成如图②的四边形，则这时窗框的形状是平行四边形，它的依据是　   　．（2）将直尺紧靠窗框的一个角（如图③），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④，说明窗框合格，这时窗框是矩形，它的依据是　   　．14．计算的结果是_____．15．已知一次函数y=kx+b的图像过点（-1,0）和点（0,2），则该一次函数的解析式是______。16．如图，∠XOY=45°，一把直角三角尺△ABC的两个顶点A、B分别在OX，OY上移动，其中AB=10，那么点O到顶点A的距离的最大值为_____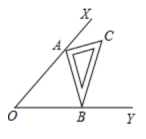． 17．如图，在△ABC中，点D、E分别在AB、AC上，∠ADE=∠C，如果AE=4cm，△ACE的面积是4cm2，四边形BCED的面积是5cm2，那么AB的长是  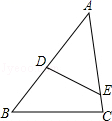       ．三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）如图，AD是△ABC的中线，AE∥BC，BE交AD于点F，且AF=DF.(1)求证:△AFE≌ODFB；(2)求证:四边形ADCE是平行四边形；(3)当AB、AC之间满足什么条件时，四边形ADCE是矩形. 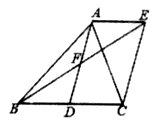  19．（5分）用无刻度的直尺绘图.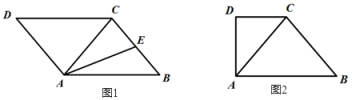（1）如图1，在中，AC为对角线，AC=BC，AE是△ABC的中线．画出△ABC的高CH（2）如图2，在直角梯形中，，AC为对角线，AC=BC，画出△ABC的高CH．   20．（8分）如图，直线L：与x轴、y轴分别交于A、B两点，在y轴上有一点C（0，4）,线段OA上的动点M（与O，A不重合）从A点以每秒1个单位的速度沿x轴向左移动。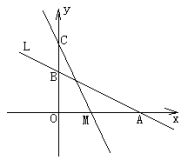（1）求A、B两点的坐标；（2）求△COM的面积S与M的移动时间t之间的函数关系式，并写出t的取值范围；（3）当t何值时△COM≌△AOB，并求此时M点的坐标。   21．（10分）如图，在平面直角坐标系中，四边形为正方形，已知点、，点、在第二象限内.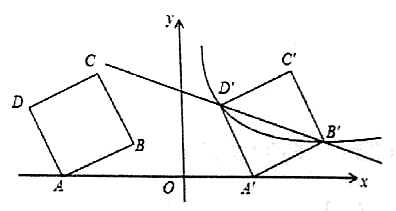（1）点的坐标___________；（2）将正方形以每秒个单位的速度沿轴向右平移秒，若存在某一时刻，使在第一象限内点、两点的对应点、正好落在某反比例函数的图象上，请求出此时的值以及这个反比例函数的解析式；（3）在（2）的情况下，问是否存在轴上的点和反比例函数图象上的点，使得以、、、四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点、的坐标；若不存在，请说明理由.   22．（10分）计算：（1）（2）6÷+（1﹣）2   23．（12分）如图，菱形的对角线和交于点，，，求和的长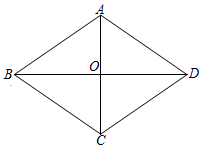．   参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、B2、D3、C4、D5、B6、D7、B8、D9、B10、B11、A12、C 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、14、 15、y=2x+216、1017、6cm． 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、（1）见解析；（2）见解析；（3）当AB=AC时，四边形ADCE是矩形.19、见解析.20、（1）A（4，0）、B（0，2）（2）当0<t<4时， S△OCM=8-2t；（3）当t=2秒时△COM≌△AOB，此时M（2，0）21、（1）点坐标为；（2），；（3）存在，，或，或，22、（1）+；（2）2+1．23、