


2022-2023学年湖北省十堰市丹江口市七下数学期末联考试题含答案
展开2022-2023学年湖北省十堰市丹江口市七下数学期末联考试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.在![]() ABCD中,∠A:∠B:∠C:∠D的值可以是( )
ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A.1:2:3:4 B.3:4:4:3 C.3:3:4:4 D.3:4:3:4
2.计算![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.11名同学参加数学竞赛初赛,他们的等分互不相同,按从高分录到低分的原则,取前6名同学参加复赛,现在小明同学已经知道自己的分数,如果他想知道自己能否进入复赛,那么还需知道所有参赛学生成绩的( )
A.平均数 B.中位数 C.众数 D.方差
4.在平面直角坐标系中,作点A(3,4)关于x轴对称的点A′,再将点A′向左平移6个单位,得到点B,则点B的坐标为( )
A.(4,-3) B.(-4,3) C.(-3,4) D.(-3,-4)
5.下列说法:![]() 矩形的对角线互相垂直且平分;
矩形的对角线互相垂直且平分;![]() 菱形的四边相等;
菱形的四边相等;![]() 一组对边平行,另一组对边相等的四边形是平行四边形;
一组对边平行,另一组对边相等的四边形是平行四边形;![]() 正方形的对角线相等,并且互相垂直平分.其中正确的个数是( )
正方形的对角线相等,并且互相垂直平分.其中正确的个数是( )
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
6.下列说法正确的是( ).
A.掷一颗骰子,点数一定小于等于6;
B.抛一枚硬币,反面一定朝上;
C.为了解一种灯泡的使用寿命,宜采用普查的方法;
D.“明天的降水概率为90%”,表示明天会有90%的地方下雨.
7.等腰三角形的底边和腰长分别是10和12,则底边上的高是( )
A.13 B.8 C.![]() D.
D.![]()
8.一个正多边形每个外角都是30°,则这个多边形边数为( )
A.10 B.11 C.12 D.13
9.如图,不等式组![]() 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.计算![]() +
+![]() 的值等于( )
的值等于( )
A.![]() B.4
B.4![]() C.5
C.5![]() D.2
D.2![]() +2
+2![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在Rt△ABC中,∠C=90°,AC=5,BC=12,则连结两条直角边中点的线段长为_______.
12.若![]() ,则m-n的值为_____.
,则m-n的值为_____.
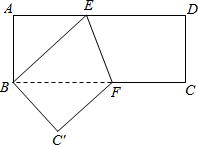
13.如图,将一张矩形纸片ABCD沿EF折叠,使点D与点B重合,点C落在C'的位置上,若∠BFE=67°,则∠ABE的度数为_____.
14.设x1,x2是一元二次方程x2﹣x﹣1=0的两根,则x1+x2+x1x2=_____.
15.已知A(﹣2,2),B(2,3),若要在x轴上找一点P,使AP+BP最短,此时点P的坐标为_____
16.已知a2-2ab+b2=6,则a-b=_________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)文具商店里的画夹每个定价为20元,水彩每盒5元,其制定两种优惠办法:①买一个面夹赠送一盒水彩;②按总价的92%付款.一美术教师欲购买画夹4个,水彩若干盒(不少于4盒),设购买水彩x盒,付款y元.
(1)试分别建立两种优惠办法中y与x的函数关系式;
(2)美术老师购买水彩30盒,通过计算说明那种方法更省钱.
18.(8分)如图,⊿![]() 是直角三角形,且
是直角三角形,且![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形,![]() 为
为![]() 的中点,
的中点,![]() 平分
平分![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
求证:![]()

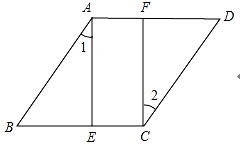
19.(8分)如图,点E,F在菱形ABCD的对边上,AE⊥BC.∠1=∠1.
(1)判断四边形AECF的形状,并证明你的结论.
(1)若AE=4,AF=1,试求菱形ABCD的面积.
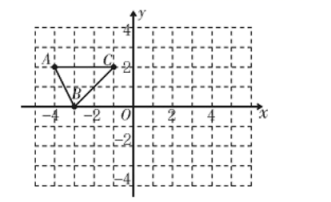
20.(8分)如图,在平面直角坐标系中,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() .
.
(1)将![]() 先向右平移4个单位长度,再向上平移2个单位长度,得到
先向右平移4个单位长度,再向上平移2个单位长度,得到![]() ,画出
,画出![]() ;
;
(2)![]() 与
与![]() 关于原点
关于原点![]() 成中心对称,画出
成中心对称,画出![]() ;
;
(3)![]() 和
和![]() 关于点
关于点![]() 成中心对称,请在图中画出点
成中心对称,请在图中画出点![]() 的位置.
的位置.
21.(8分)如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 的中点,连接
的中点,连接![]() 并延长与
并延长与![]() 的延长线相交于点
的延长线相交于点![]() .
.
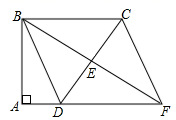
(1)求证:四边形![]() 是平行四边形;(2)若
是平行四边形;(2)若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
22.(10分)已知平行四边形ABCD的两边AB、BC的长是关于x的方程x2-mx+![]() -
-![]() =0的两个实数根.
=0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么平行四边形ABCD的周长是多少?
23.(10分)已知x=![]() +1 , y=
+1 , y=![]() -1 , 求x2+xy+y2的值.
-1 , 求x2+xy+y2的值.
24.(12分)垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
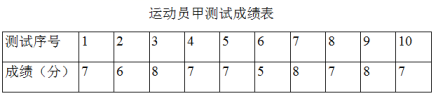
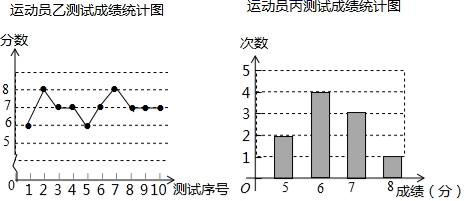
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
参考答案
一、选择题(每小题3分,共30分)
1、D
2、A
3、B
4、D
5、B
6、A
7、D
8、C
9、B
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、6.5
12、4
13、44°
14、1
15、(-0.4,0)
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、 (1)见解析;(2)①更省钱.
18、证明见解析.
19、四边形AECF是矩形,理由见解析;(1)菱形ABCD的面积=10.
20、(1)详见解析;(2)详见解析;(3)详见解析
21、(1)见解析;(2)四边形![]() 的面积
的面积![]() .
.
22、(1)m=1时,四边形ABCD是菱形,菱形ABCD的边长是![]() ;(2)平行四边形ABCD的周长是1.
;(2)平行四边形ABCD的周长是1.
23、7
24、(1)众数是7,中位数是7;(2)乙,理由见解析












