


2022-2023学年浙江省嘉兴市十学校七年级数学第二学期期末达标检测模拟试题含答案
展开这是一份2022-2023学年浙江省嘉兴市十学校七年级数学第二学期期末达标检测模拟试题含答案,共8页。试卷主要包含了如图,丝带重叠的部分一定是等内容,欢迎下载使用。
2022-2023学年浙江省嘉兴市十学校七年级数学第二学期期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.已知一组数据共有![]() 个数,前面
个数,前面![]() 个数的平均数是
个数的平均数是![]() ,后面
,后面![]() 个数的平均数是
个数的平均数是![]() ,则这
,则这![]() 个数的平均数是( )
个数的平均数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.直角三角形中,两直角边分别是6和8.则斜边上的中线长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.如图,在平面直角坐标系中,一次函数![]() 经过
经过![]() ,
,![]() 两点,则不等式
两点,则不等式![]() 的解是
的解是![]()
![]()

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如图,在锐角三角形ABC中,AB=![]() ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
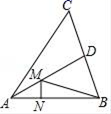
A.4 B.5 C.6 D.10
5.如图,丝带重叠的部分一定是( )

A.菱形 B.矩形 C.正方形 D.都有可能
6.在四边形![]() 中,
中,![]() ,再补充一个条件使得四边形
,再补充一个条件使得四边形![]() 为菱形,这个条件可以是( )
为菱形,这个条件可以是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 与
与![]() 互相平分
互相平分
7.如图,矩形![]() 的对角线
的对角线![]() 相交于点
相交于点![]() ,
,![]() ,则
,则![]() 的周长为()
的周长为()
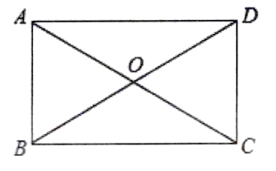
A.12 B.14 C.16 D.18
8.若二次根式![]() 在实数范围内有意义,则a的取值范围是( )
在实数范围内有意义,则a的取值范围是( )
A.a>1 B.a≥1 C.a=1 D.a≤1
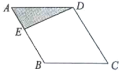
9.如图,点![]() 为菱形
为菱形![]() 边上的一个动点,并沿
边上的一个动点,并沿![]() →
→![]() →
→![]() →
→![]() 的路径移动,设点E经过的路径长为
的路径移动,设点E经过的路径长为![]() ,
,![]() 的面积为
的面积为![]() ,则下列图象能大致反映
,则下列图象能大致反映![]() 与
与![]() 的函数关系的是( )
的函数关系的是( )
A.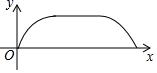 B.
B.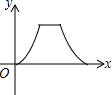
C.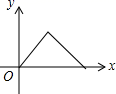 D.
D.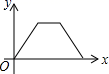
10.把一元二次方程2x2-3x-1=0配方后可得( )
A.![]()
![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在学校的卫生检查中,规定各班的教室卫生成绩占30%,环境卫生成绩占40%,个人卫生成绩占30%.八年级一班这三项成绩分别为85分,90分和95分,求该班卫生检查的总成绩_____.
12.已知![]() 是一次函数,则
是一次函数,则![]() __________.
__________.
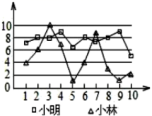
13.小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,根据图中的信息,成绩较稳定的是____.
14.如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是__.
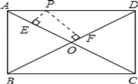
15.已知,![]() ,则
,则![]() ______.
______.
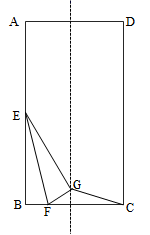
16.如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 是
是![]() 边上的一动点,将
边上的一动点,将![]() 沿
沿![]() 折叠,使得点
折叠,使得点![]() 落在
落在![]() 处,连接
处,连接![]() ,
,![]() ,当点
,当点![]() 落在矩形
落在矩形![]() 的对称轴上,则
的对称轴上,则![]() 的值为______.
的值为______.
三、解下列各题(本大题共8小题,共72分)
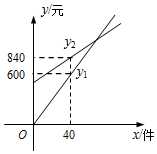
17.(8分)某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少8元.从图中信息解答如下问题(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用):
(1)求y1的函数解析式;
(2)请问方案二中每月付给销售人员的底薪是多少元?
(3)小丽应选择哪种销售方案,才能使月工资更多?
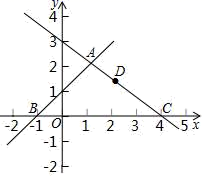
18.(8分)如图,在平面直角坐标系可中,直线y=x+1与y=﹣![]() x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
(1)求点A,B,C的坐标;
(2)在直线AB上是否存在点E使得四边形EODA为平行四边形?存在的话直接写出![]() 的值,不存在请说明理由;
的值,不存在请说明理由;
(3)当△CBD为等腰三角形时直接写出D坐标.
19.(8分)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒
点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒![]() 过点D作
过点D作![]() 于点F,连接DE、EF.
于点F,连接DE、EF.
![]() 求证:
求证:![]() ;
;
![]() 四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
![]() 当t为何值时,
当t为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
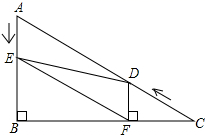
20.(8分)解不等式组: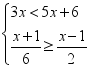 ,把它的解集在数轴上表示出来,并写出其整数解.
,把它的解集在数轴上表示出来,并写出其整数解.
21.(8分)平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”的
对于图形![]() 和图形
和图形![]() ,若图形
,若图形![]() 和图形
和图形![]() 分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形
分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形![]() 和图形
和图形![]() 是“中心轴对称”的.
是“中心轴对称”的.
特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的.
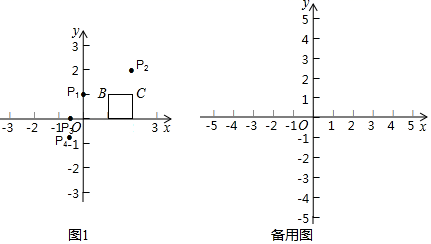
(1)如图1,在正方形ABCD中,点![]() ,点
,点![]() ,
,
①下列四个点![]() ,
,![]() ,
,![]() ,
,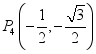 中,与点A是“中心轴对称”的是________;
中,与点A是“中心轴对称”的是________;
②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标![]() 的取值范围;
的取值范围;
(2)四边形GHJK的四个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,一次函数
,一次函数![]() 图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围.
图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围.
22.(10分)先化简再求值:![]() ,其中a=3.
,其中a=3.
23.(10分)计算:(- ![]() )2×(
)2×( ![]() )-2+(-2019)0
)-2+(-2019)0
24.(12分)(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
| 空调 | 彩电 |
进价(元/台) | 5400 | 3500 |
售价(元/台) | 6100 | 3900 |
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、D
4、B
5、A
6、D
7、A
8、B
9、D
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、90分.
12、![]()
13、小明
14、4.1
15、-5
16、2
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() ;(2)方案二中每月付给销售人员的底薪是560元;(3)当销售件数少于70件时,提成方案二好些;当销售件数等于70件时,两种提成方案一样;当销售件数多于70件时,提成方案一好些.
;(2)方案二中每月付给销售人员的底薪是560元;(3)当销售件数少于70件时,提成方案二好些;当销售件数等于70件时,两种提成方案一样;当销售件数多于70件时,提成方案一好些.
18、 (1)A(![]() ,
,![]() ),B(﹣1,0),C(4,0);(2)存在,
),B(﹣1,0),C(4,0);(2)存在,![]() =
=![]() ;(3)点D的坐标为(﹣
;(3)点D的坐标为(﹣![]() ,
,![]() )或(8,﹣3)或(0,3)或(
)或(8,﹣3)或(0,3)或(![]() ,
,![]() ).
).
19、(1)证明见解析;(2)能,理由见解析;(3)![]() 秒或4秒时,
秒或4秒时,![]() 为直角三角形.
为直角三角形.
20、![]() ,x的整数解为﹣1,﹣1,0,1,1.
,x的整数解为﹣1,﹣1,0,1,1.
21、(1)①P1,P1;②![]() ≤xE≤
≤xE≤![]() ;(2)2
;(2)2![]() ≤b≤2+2
≤b≤2+2![]() 或-2-2
或-2-2![]() ≤b≤-2
≤b≤-2![]() .
.
22、![]() ,
,![]() .
.
23、2
24、解:(1)设商场计划购进空调x台,则计划购进彩电(30﹣x)台,由题意,得
y=(6100﹣5400)x+(3900﹣3500)(30﹣x)=300x+12000。
(2)依题意,得![]() ,
,
解得10≤x≤![]() 。
。
∵x为整数,∴x=10,11,12。∴商场有三种方案可供选择:
方案1:购空调10台,购彩电20台;
方案2:购空调11台,购彩电19台;
方案3:购空调12台,购彩电18台。
(3)∵y=300x+12000,k=300>0,∴y随x的增大而增大。
∴当x=12时,y有最大值,y最大=300×12+12000=15600元.
故选择方案3:购空调12台,购彩电18台时,商场获利最大,最大利润是15600元。
相关试卷
这是一份浙江省嘉兴市十学校2023-2024学年数学九年级第一学期期末达标检测试题含答案,共8页。
这是一份辽宁省红旗学校2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案,共7页。试卷主要包含了使有意义的的取值范围是,已知二次函数等内容,欢迎下载使用。
这是一份浙江省嘉兴市海盐县2022-2023学年七年级数学第二学期期末复习检测模拟试题含答案,共7页。试卷主要包含了下列说法中,正确的是等内容,欢迎下载使用。












