


浙江省嘉兴市南湖区北师大南湖附校2022-2023学年数学七下期末达标检测模拟试题含答案
展开浙江省嘉兴市南湖区北师大南湖附校2022-2023学年数学七下期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.下列各图象中,( )表示y是x的一次函数.
A.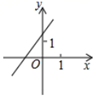 B.
B.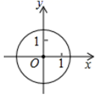
C.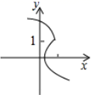 D.
D.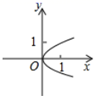
2.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AB=BC C.AC⊥BD D.AC=BD
3.今年我市某县6月1日到10日的每一天最高气温变化如折线图所示,则这10个最高气温的中位数和众数分别是( )
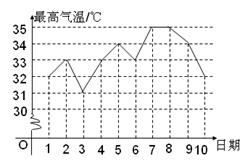
A.33℃ 33℃ B.33℃ 32℃ C.34℃ 33℃ D.35℃ 33℃
4.如图(图在第二页)所示是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是
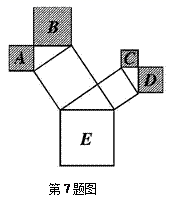
A.13 B.26 C.47 D.94
5.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则y1,y2,0的大小关系是( )
A.0<y1<y2 B.y1<0<y2
C.y1<y2<0 D.y2<0<y1
6.如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 上的一点,设
上的一点,设![]() ,则
,则![]() 的面积
的面积![]() 与
与![]() 之间的函数关系式是
之间的函数关系式是![]()
![]()
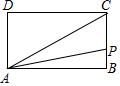
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.教练要从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛.两人在形同条件下各打了5发子弹,命中环数如下:甲:9、8、7、7、9;乙:10、8、9、7、1.应该选( )参加.
A.甲 B.乙 C.甲、乙都可以 D.无法确定
8.下列方程中,有实数根的方程是( )
A.x4+16=0 B.x2+2x+3=0 C.![]() D.
D.![]()
9.下列说法中正确的是( )
A.有一个角是直角的四边形是矩形
B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相垂直平分的四边形是正方形
D.两条对角线相等的菱形是正方形
10.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120° 的菱形,剪口与第二次折痕所成角的度数应为
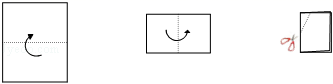
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
二、填空题(本大题共有6小题,每小题3分,共18分)
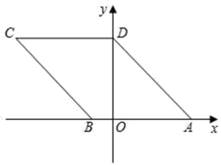
11.如图,若菱形ABCD的顶点A,B的坐标分别为(4,0),(﹣1,0),点D在y轴上,则点C的坐标是_____.
12.分解因式:x2-2x+1=__________.
13.已知直线![]() 在
在![]() 轴上的截距是-2,且与直线
轴上的截距是-2,且与直线![]() 平行,那么该直线的解析是______
平行,那么该直线的解析是______
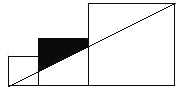
14.将边长分别为2、3、5的三个正方形按图所示的方式排列,则图中阴影部分的面积为 .
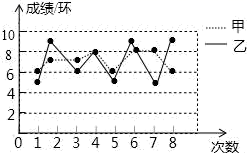
15.甲乙两人8次射击的成绩如图所示(单位:环)根据图中的信息判断,这8次射击中成绩比较稳定的是______(填“甲”或“乙”)
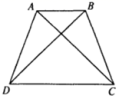
16.如图,在等腰梯形ABCD中,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积为__________cm1.
三、解下列各题(本大题共8小题,共72分)
17.(8分)实践与探究
宽与长的比是![]() (约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
(约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
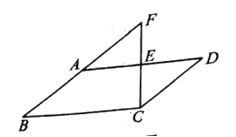
下面我们通过折纸得到黄金矩形。
第一步,在一张矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平。
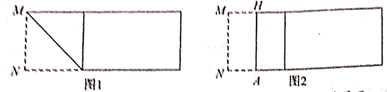
第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平,折痕是![]() 。
。
第三步,折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处,折痕为
处,折痕为![]() 。
。
第四步,展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ;过点
;过点![]() 折出折痕
折出折痕![]() ,使
,使![]() 。
。
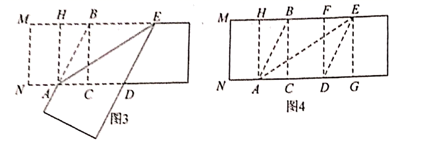
(1)上述第三步将![]() 折到
折到![]() 处后,得到一个四边形
处后,得到一个四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由。
的形状,并说明理由。
(2)上述第四步折出折痕![]() 后得到一个四边形
后得到一个四边形![]() ,这个四边形是黄金矩形,请你说明理由。(提示:设
,这个四边形是黄金矩形,请你说明理由。(提示:设![]() 的长度为2)
的长度为2)
(3)在图4中,再找出一个黄金矩形_______________________________(黄金矩形![]() 除外,直接写出答案,不需证明,可能参考数值:
除外,直接写出答案,不需证明,可能参考数值:![]() )
)
(4)请你举一个采用了黄金矩形设计的世界名建筑_________________________.
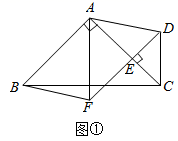
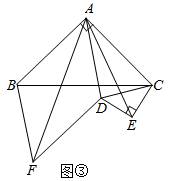
18.(8分)如图![]() ,在等腰
,在等腰![]() 中,
中,![]() ,点E在AC上
,点E在AC上![]() 且不与点A、C重合
且不与点A、C重合![]() ,在
,在![]() 的外部作等腰
的外部作等腰![]() ,使
,使![]() ,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
![]() 请直接写出线段AF,AE的数量关系;
请直接写出线段AF,AE的数量关系;
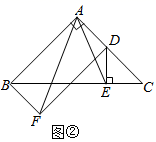
![]() 将
将![]() 绕点C逆时针旋转,当点E在线段BC上时,如图
绕点C逆时针旋转,当点E在线段BC上时,如图![]() ,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
![]() 若
若![]() ,
,![]() ,在图
,在图![]() 的基础上将
的基础上将![]() 绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
19.(8分)我们可用![]() 表示以
表示以![]() 为自变量的函数,如一次函数
为自变量的函数,如一次函数![]() ,可表示为
,可表示为![]() ,且
,且![]() ,
,![]() ,定义:若存在实数
,定义:若存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点,例如:
的不动点,例如:![]() ,令
,令![]() ,得
,得![]() ,那么
,那么![]() 的不动点是1.
的不动点是1.
(1)已知函数![]() ,求
,求![]() 的不动点.
的不动点.
(2)函数![]() (
(![]() 是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;
是常数)的图象上存在不动点吗?若存在,请求出不动点;若不存在,请说明理由;
(3)已知函数![]() (
(![]() ),当
),当![]() 时,若一次函数
时,若一次函数![]() 与二次函数
与二次函数![]() 的交点为
的交点为![]() ,即
,即![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且
的不动点,且![]() 两点关于直线
两点关于直线![]() 对称,求
对称,求![]() 的取值范围.
的取值范围.
20.(8分)某区举行“庆祝改革开放40周年”征文比赛,已知每篇参赛征文成绩记![]() 分
分![]() ,组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表:
,组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表:
征文比赛成绩频数分布表 | ||
分数段 | 频数 | 频率 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 |
| 1 |
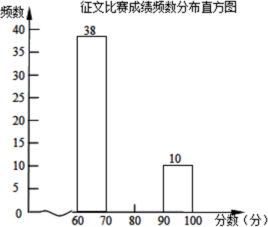
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中![]() 的值是 ;
的值是 ;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
21.(8分)先化简,再求值:(1﹣![]() )÷
)÷![]() .其中a从0,1,2,﹣1中选取.
.其中a从0,1,2,﹣1中选取.
22.(10分)如图,在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 的延长线相交于点
的延长线相交于点![]() ,
,
(1)求证:![]() ;
;
(2)若![]() ,
,![]() 且
且![]() ,求
,求![]() 的长.
的长.
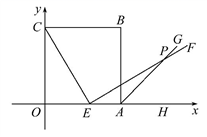
23.(10分)如图,边长为5的正方形OABC的顶点O在坐标原点处,点A,C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AG交于点P.
(1)求证:CE=EP.
(2)若点E的坐标为(3,0),在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,求出点M的坐标;若不存在,说明理由.
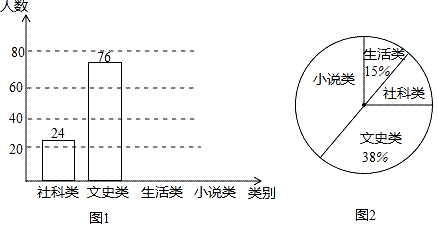
24.(12分)央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、D
3、A
4、C
5、B
6、D
7、A
8、C
9、D
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、(﹣5,3)
12、(x-1)1.
13、![]()
14、![]()
15、甲
16、2
三、解下列各题(本大题共8小题,共72分)
17、(1)四边形![]() 是菱形,见解析;(2)见解析;(3)黄金矩形
是菱形,见解析;(2)见解析;(3)黄金矩形![]() (或黄金矩形
(或黄金矩形![]() );(4)希腊的巴特农神庙(或巴黎圣母院).
);(4)希腊的巴特农神庙(或巴黎圣母院).
18、(1)证明见解析;(2)①![]() ②
②![]() 或
或![]() .
.
19、(1![]() 的不动点为0和2;(2)①
的不动点为0和2;(2)①![]() 时,有唯一的不动点
时,有唯一的不动点![]() ②
②![]() 时,有无数个不动点③
时,有无数个不动点③![]() 时,没有不动点;(3)
时,没有不动点;(3)![]() 的取值范围是
的取值范围是![]()
20、(1)0.2;(2)见解析;(3)300篇.
21、![]() ,
,![]()
22、(1)见解析;(2)![]() .
.
23、(1)证明见解析;(2)存在点M的坐标为(0,2).
24、(1)200;(2)补图见解析;(3)12;(4)300人.
2025届浙江省嘉兴市南湖区实验数学九年级第一学期开学达标检测模拟试题【含答案】: 这是一份2025届浙江省嘉兴市南湖区实验数学九年级第一学期开学达标检测模拟试题【含答案】,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙江省嘉兴市南湖区北师大南湖附校2023-2024学年数学九上期末学业水平测试模拟试题含答案: 这是一份浙江省嘉兴市南湖区北师大南湖附校2023-2024学年数学九上期末学业水平测试模拟试题含答案,共7页。试卷主要包含了若二次函数的图象经过点,在平面直角坐标系中,点P等内容,欢迎下载使用。
浙江省嘉兴市南湖区北师大南湖附校2023-2024学年数学九年级第一学期期末达标测试试题含答案: 这是一份浙江省嘉兴市南湖区北师大南湖附校2023-2024学年数学九年级第一学期期末达标测试试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,抛物线y=﹣,关于的一元二次方程根的情况是,下列事件中,是必然事件的是等内容,欢迎下载使用。












