2022-2023学年河南郑州七下数学期末综合测试模拟试题含答案

这是一份2022-2023学年河南郑州七下数学期末综合测试模拟试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，下列各式中，化简后能与合并的是，下列条件中能构成直角三角形的是，下列说法中，正确的是等内容，欢迎下载使用。
2022-2023学年河南郑州七下数学期末综合测试模拟试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1．已知是一次函数的图象上的两个点，则的大小关系是（  ）A． B． C． D．不能确定2．如图，正方形ABCD的边长为1，其面积标记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2，…，按照此规律继续下去，则S2018的值为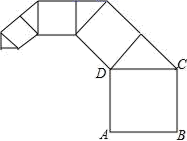（　　）A． B． C． D．3．甲、乙、丙三人进行射击测试，每人10次射击的平均成绩恰好都是9.2环，方差分别是，.，在本次射击测试中，成绩最稳定的是（   ）A．甲 B．乙 C．丙 D．无法确定 4．一艘轮船和一艘快艇沿相同路线从甲港岀发匀速行驶至乙港，行驶路程随时间变化的图象如图，则下列结论错误的是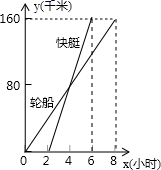（　　）A．轮船的速度为20千米时 B．轮船比快艇先出发2小时C．快艇到达乙港用了6小时 D．快艇的速度为40千米时5．下列各式中，化简后能与合并的是(  )A． B． C． D．6．用配方法解方程x2-8x+9=0时，原方程可变形为（　　）A．（x-4）2=9 B．（x-4）2=7 C．（x-4）2=-9 D．（x-4）2=-77．下列条件中能构成直角三角形的是（         ）A．a＝3，b＝4，c＝6 B．a＝5，b＝6，c＝7C．a＝6，b＝8，c＝9 D．a＝5，b＝12，c＝138．在同一平面直角坐标系中，函数与的图象大致是（    ）A． B． C． 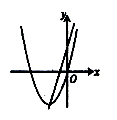D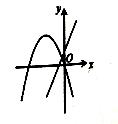．9．为迎接“义务教育均衡发展”检查，我市抽查了某校七年级8个班的班额人数，抽查数据统计如下：52,49,56,54,52,51,55,54，这四组数据的众数是（ ）A．52和54    B．52C．53    D．5410．下列说法中，正确的是（    ）A．有两边相等的平行四边形是菱形B．两条对角线互相垂直平分的四边形是菱形C．两条对角线相等且互相平分的四边形是菱形D．四个角相等的四边形是菱形二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，正方形AFCE中，D是边CE上一点，把绕点A顺时针旋转90°，点D对应点交CF延长线于点B，若四边形ABCD的面积是、则AC长__________cm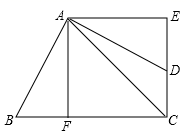．12．一般地，在平面直角坐标系中，我们求点到直线间的距离，可用下面的公式求解：点到直线的距离公式是：如：求：点到直线的距离．解：由点到直线的距离公式，得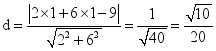根据平行线的性质，我们利用点到直线的距离公式，也可以求两平行线间的距离．则两条平行线：和：间的距离是______．13．如图，在平面直角坐标系中，菱形ABCD的顶点A在y轴上，且点A坐标为（0，4），BC在x轴正半轴上，点C在B点右侧，反比例函数（x＞0）的图象分别交边AD，CD于E，F，连结BF，已知，BC=k，AE=CF，且S四边形ABFD=20，则k= _________． 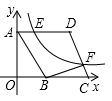14．若关于的方程的解为正数，则的取值范围是__________.15．使式子的值为0，则a的值为_______.16．已知命题：全等三角形的对应角相等.这个命题的逆命题是：__________．三、解下列各题(本大题共8小题，共72分)17．（8分）某校为灾区开展了“献出我们的爱”赈灾捐款活动，九年级（1）班50名同学积极参加了这次赈灾捐款活动，因不慎，表中数据有一处被墨水污染，已无法看清，但已知全班平均每人捐款38元.捐款（元）101530 5060人数361111136（1）根据以上信息可知，被污染处的数据为     .（2）该班捐款金额的众数为     ，中位数为     .（3）如果用九年级（1）班捐款情况作为一个样本，请估计全校2000人中捐款在40元以上（包括40元）的人数是多少？   18．（8分）如图，在平直角坐标系xOy中，直线与反比例函数的图象关于点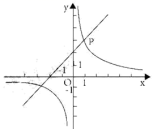（1）求点P的坐标及反比例函数的解析式；（2）点是x轴上的一个动点，若，直接写出n的取值范围．   19．（8分）为了解某校八年级男生的体能情况，体育老师随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制成图1和图2两幅尚不完整的统计图．(1)本次抽测的男生有　   人，抽测成绩的众数是　   ； (2)请你将图2的统计图补充完整；(3)若规定引体向上5次以上（含5次）为体能达标，则该校400名八年级男生中估计有多少人体能达标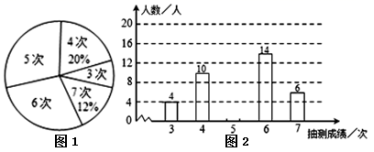？   20．（8分）（1）如图1，正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，延长CD到点G，使DG=BE，连结EF，AG．求证：①∠BEA =∠G，② EF=FG．（2）如图2，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°，若BM=1，CN=3，求MN的长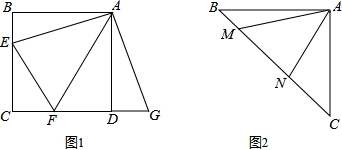．   21．（8分）目前节能灯在城市已基本普及，今年山东省面向县级及农村地区推广,为响应号召，某商场计划购进甲，乙两种节能灯共只，这两种节能灯的进价、售价如下表: 进价（元/只）售价（元/只）甲型乙型 (1)如何进货，进货款恰好为元?(2)设商场购进甲种节能灯只，求出商场销售完节能灯时总利润与购进甲种节能灯之间的函数关系式;(3)如何进货，商场销售完节能灯时获利最多且不超过进货价的，此时利润为多少元？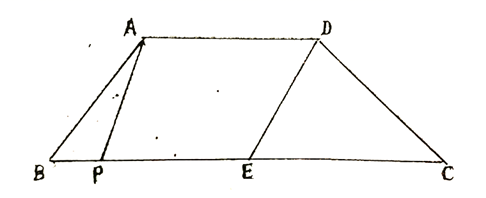   22．（10分）计算：2÷×．   23．（10分）如图，在梯形中中，，是的中点，，，，，点是边上一动点，设的长为.（1）当的值为多少时，以点为顶点的三角形为直角三角形；（2）当的值为多少时，以点为顶点的四边形为平行四边形；（3）点在边上运动的过程中，以为顶点的四边形能否构成菱形？试说明理由.   24．（12分）在数学拓展课上，老师让同学们探讨特殊四边形的做法：如图，先作线段，作射线（为锐角），过作射线平行于，再作和的平分线分别交和于点和，连接，则四边形为菱形；（1）你认为该作法正确吗？请说明理由.（2）若，并且四边形的面积为，在上取一点，使得.请问图中存在这样的点吗？若存在，则求出的长；若不存在，请说明理由.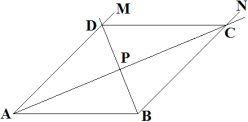   参考答案 一、选择题(每小题3分,共30分)1、C2、B3、B4、C5、B6、B7、D8、C9、A10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、212、13、14、且15、16、对应角相等的三角形全等 三、解下列各题(本大题共8小题，共72分)17、（1）40；（2）50，40；（3）1200人18、（1）；（2）19、（1）50，5次；（2）见解析；（3）该校400名八年级男生中有288人体能达标20、（1）①见解析②见解析（1）21、（1）乙型节能灯为800； （2）； （3）购进乙型节能灯只时的最大利润为元.22、24．23、（1）当的值为3或8时，以点为顶点的三角形为直角三角形；（2）当的值为1或11时，以点为顶点的四边形为平行四边形；（3）以点为顶点的四边形能构成菱形，理由详见解析.24、（1）作法正确（2）或