


2022-2023学年河北省张家口市第一中学数学七下期末经典模拟试题含答案
展开2022-2023学年河北省张家口市第一中学数学七下期末经典模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,![]() 为
为![]() 的平分线,
的平分线,![]() 于
于![]() ,
,![]() ,
,![]() ,则点
,则点![]() 到射线
到射线![]() 的距离为( )
的距离为( )
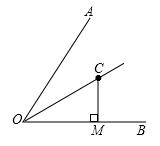
A.2 B.3 C.4 D.5
2.下列二次根式中,不能与![]() 合并的是( )
合并的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.如图,线段AB两端点的坐标分别为A(-1,0),B(1,1),把线段AB平移到CD位置,若线段CD两端点的坐标分别为C(1,a),D(b,4),则a+b的值为( )
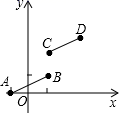
A.7 B.6 C.5 D.4
4.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=( )
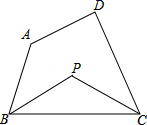
A.90°-![]() α B.90°+
α B.90°+ ![]() α C.
α C.![]() D.360°-α
D.360°-α
5.一次函数![]() 的图象经过( )
的图象经过( )
A.一、二、三象限 B.一、二、四象限
C.二、三、四象限 D.一、三、四象限
6.若![]() ,则下列式子成立的是( )
,则下列式子成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.如图,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,过点
的中点,过点![]() 作
作![]() ∥
∥![]() 交
交![]() 的延长线于点
的延长线于点![]() ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )

A.![]() B.
B.![]()
C.![]() <
<![]() D.
D.![]() >
>![]()
8.下列四个图形分别是四届国际数学家大会的会标,其中不属于中心对称图形的是( )
A.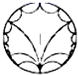 B.
B. C.
C. D.
D.
9.直线y=kx+b不经过第三象限,则k、b应满足( )
A.k>0,b<0 B.k<0,b>0 C.k<0 b<0 D.k<0,b≥0
10.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长是( )
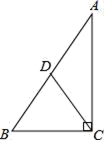
A.6 B.5 C.4 D.3
11.如表记录了甲、乙、丙、丁四名学生最近几次数学综合测试成绩的平均数与方差:
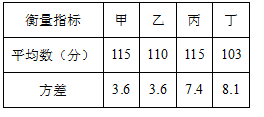
根据表中数据,要从中选择一名成好且发挥稳定的同学参加竟赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
12.如图,△ABC中,CD⊥AB于D,且E是AC的中点.若AD=6,DE=5,则CD的长等于( )
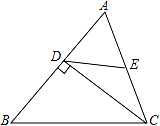
A.7 B.8 C.9 D.10
二、填空题(每题4分,满分20分,将答案填在答题纸上)
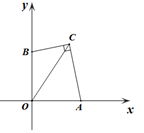
13.如图,在平面直角坐标系xOy中,A,B两点分别在x轴,y轴的正半轴上,且OA=OB,点C在第一象限,OC=3,连接BC,AC,若∠BCA=90°,则BC+AC的值为_________.
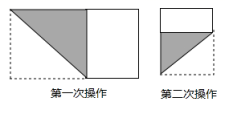
14.把长为20,宽为a的长方形纸片(10<a<20),如图那样折一下,剪下一个边长等于长方形宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如此反复操作下去,若在第n次操作后,剩下的长方形为正方形,则操作停止.当n=3时,a的值为________.
15.如图,已知等边![]() 的边长为8,
的边长为8,![]() 是中线
是中线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 下方作等边
下方作等边![]() ,连接
,连接![]() 并延长至点
并延长至点![]() 为
为![]() 上一点,且
上一点,且![]() ,则
,则![]() 的长为_________.
的长为_________.
16.计算:(﹣4ab2)2÷(2a2b)0=_____.
17.如果![]() +
+![]() =2012,
=2012, ![]() -
-![]() =1,那么
=1,那么![]()
![]() =_________.
=_________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)某数码专营店销售甲、乙两种品牌智能手机,这两种手机的进价和售价如下表所示:
| 甲 | 乙 |
进价(元/部) | 4300 | 3600 |
售价(元/部) | 4800 | 4200 |
(1)该店销售记录显示.三月份销售甲、乙两种手机共17部,且销售甲种手机的利润恰好是销售乙种手机利润的2倍,求该店三月份售出甲种手机和乙种手机各多少部?
(2)根据市场调研,该店四月份计划购进这两种手机共20部,要求购进乙种手机数不超过甲种手机数的![]() ,而用于购买这两种手机的资金低于81500元,请通过计算设计所有可能的进货方案.
,而用于购买这两种手机的资金低于81500元,请通过计算设计所有可能的进货方案.
(3)在(2)的条件下,该店打算将四月份按计划购进的20部手机全部售出后,所获得利润的30%用于购买A,B两款教学仪器捐赠给某希望小学.已知购买A仪器每台300元,购买B仪器每台570元,且所捐的钱恰好用完,试问该店捐赠A,B两款仪器一共多少台?(直接写出所有可能的结果即可)
19.(5分)先化简,再求值: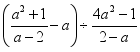 ,其中
,其中![]() 是满足不等式组
是满足不等式组![]() 的整数解.
的整数解.
20.(8分)世界上大部分国家都使用摄氏温度(℃),但美国,英国等国家的天气预报都使用华氏温度(℉),两种计量之间有如下对应:
摄氏温度(℃) | … | 0 | 10 | … |
华氏温度(℉) | … | 32 | 50 | … |
已知华氏温度y(℉)是摄氏温度x(℃)的一次函数.
求该一次函数的解析式;
当华氏温度14℉时,求其所对应的摄氏温度.
21.(10分)问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
类比探究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)
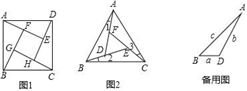
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.
(2)△DEF是否为正三角形?请说明理由.
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.
22.(10分)计算题
(1)因式分解:1a2b﹣6ab2+1b1
(2)解不等式组: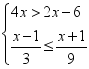
(1)先化简,再求值:(1+![]() )÷
)÷![]() ,其中a=﹣1.
,其中a=﹣1.
23.(12分)学校为了提高学生跳远科目的成绩,对全校500名九年级学生开展了为期一个月的跳远科目强化训练.王老师为了了解学生的训练情况,强化训练前,随机抽取了该年级部分学生进行跳远测试,经过一个月的强化训练后,再次测得这部分学生的成绩,将两次测得的成绩制作成如图所示的统计图和不完整的统计表
训练后学生成绩统计表
成绩/分数 | 6分 | 7分 | 8分 | 9分 | 10分 |
人数/人 | 1 | 3 | 8 | 5 | n |
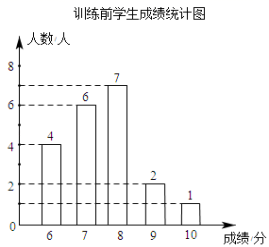
根据以上信息回答下列问题
(1)训练后学生成绩统计表中n= ,并补充完成下表:
| 平均分 | 中位数 | 众数 |
训练前 | 7.5 |
| 8 |
训练后 |
| 8 |
|
(2)若跳远成绩9分及以上为优秀,估计该校九年级学生训练后比训练前达到优秀的人数增加了多少?
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、C
3、B
4、C
5、D
6、B
7、B
8、A
9、D.
10、C
11、A
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、12或2
15、1
16、16a2b1
17、1.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)售出甲手机12部,乙手机5部;可能的方案为:①购进甲手机12部,乙手机8部;②购进甲手机13部,乙手机7部;(3)该店捐赠A,B两款仪器一共9台或8台.
19、化简得:![]() 求值得:
求值得:![]() .
.
20、(1)y=1.8x+1;(2)华氏温度14℉所对应的摄氏温度是-2℃.
21、 (1)见解析;(1)△DEF是正三角形;理由见解析;(3)c1=a1+ab+b1
22、(2)2b(a﹣b)2;(2)﹣2<x≤2;(2)a+2;﹣2.
23、(1)3;7.5;8.3;8;(2)估计该校九年级学生训练后比训练前达到优秀的人数增加了125人
2022-2023学年黑龙江省鸡西中学数学七下期末经典模拟试题含答案: 这是一份2022-2023学年黑龙江省鸡西中学数学七下期末经典模拟试题含答案,共7页。试卷主要包含了若,则的值是,下列事件中是必然事件的是,计算等内容,欢迎下载使用。
2022-2023学年重庆市育才中学数学七下期末经典模拟试题含答案: 这是一份2022-2023学年重庆市育才中学数学七下期末经典模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,函数y=中自变量x的取值范围是等内容,欢迎下载使用。
2022-2023学年湖北省恩施州东城中学数学七下期末经典模拟试题含答案: 这是一份2022-2023学年湖北省恩施州东城中学数学七下期末经典模拟试题含答案,共7页。试卷主要包含了下列计算错误的是,使代数式有意义的x的取值范围,某居民今年1至6月份等内容,欢迎下载使用。












