


2022-2023学年河北省保定市雄县七下数学期末监测试题含答案
展开2022-2023学年河北省保定市雄县七下数学期末监测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.如果a为任意实数, 下列各式中一定有意义的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是( )
A.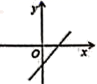 B.
B.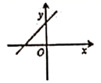 C.
C.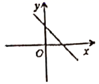 D.
D.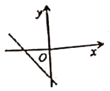
3.要使式子![]() 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A.x>0 B.x≥﹣3 C.x≥3 D.x≤3
4.多项式 x2 4 因式分解的结果是( )
A.x 22 B.x 22 C.x 2x 2 D.x 4x 4
5.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )
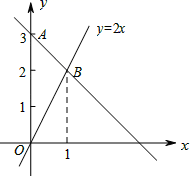
A.y=2x+3 B.y=x﹣3 C.y=2x﹣3 D.y=﹣x+3
6.下列二次根式中,属于最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.下列事件是确定事件的是( )
A.射击运动员只射击1次,就命中靶心
B.打开电视,正在播放新闻
C.任意一个三角形,它的内角和等于180°
D.抛一枚质地均匀的正方体骰子,朝上一面的点数为6
8.矩形的对角线一定( )
A.互相垂直平分且相等 B.互相平分且相等
C.互相垂直且相等 D.互相垂直平分
9.下列等式从左到右的变形,属于因式分解的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.关于一个四边形是不是正方形,有如下条件①对角线互相垂直且相等的平行四边形;②对角线互相垂直的矩形;③对角线相等的菱形;④对角线互相垂直平分且相等的四边形;以上条件,能判定正方形的是( )
A.①②③ B.②③④ C.①③④ D.①②③④
二、填空题(本大题共有6小题,每小题3分,共18分)
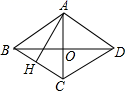
11.如图,在菱形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,已知BO=4,S菱形ABCD=24,则
,已知BO=4,S菱形ABCD=24,则![]() ___.
___.
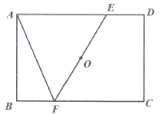
12.如图,在矩形![]() 中,
中,![]() ,过矩形
,过矩形![]() 的对角线交点
的对角线交点![]() 作直线分别交
作直线分别交![]() 、
、![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() ____.
____.
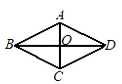
13.如图,菱形ABCD的周长为12,∠B=60°,则菱形的面积为_________m2
14.有甲、乙两张纸条,甲纸条的宽度是乙纸条宽的2倍,如图,将这两张纸条交叉重叠地放在一起,重合部分为四边形ABCD.则AB与BC的数量关系为 .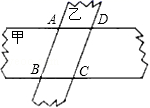
15.函数![]() 中自变量x的取值范围是_______.
中自变量x的取值范围是_______.
16.在●〇●〇〇●〇〇〇●〇〇〇〇●〇〇〇〇〇中,空心圈“〇”出现的频率是_____.
三、解下列各题(本大题共8小题,共72分)
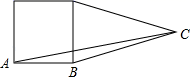
17.(8分)(1)计算:40372﹣4×2018×2019;
(2)将边长为1的一个正方形和一个底边为1的等腰三角形如图摆放,求△ABC的面积.
18.(8分)数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=1.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
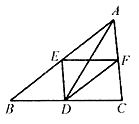
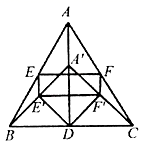
19.(8分)在![]() 中,D,E,F分别是三边
中,D,E,F分别是三边![]() ,
,![]() ,
,![]() 上的中点,连接
上的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,已知
,已知![]() .
.
(1)观察猜想:如图,当![]() 时,①四边形
时,①四边形![]() 的对角线
的对角线![]() 与
与![]() 的数量关系是________;②四边形
的数量关系是________;②四边形![]() 的形状是_______;
的形状是_______;
(2)数学思考:如图,当![]() 时,(1)中的结论①,②是否发生变化?若发生变化,请说明理由;
时,(1)中的结论①,②是否发生变化?若发生变化,请说明理由;
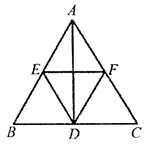
(3)拓展延伸:如图,将上图的点A沿![]() 向下平移到
向下平移到![]() 点,使得
点,使得![]() ,已知
,已知![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求四边形
的中点,求四边形![]() 与四边形
与四边形![]() 的面积比.
的面积比.
20.(8分)某校餐厅计划购买12张餐桌和一批餐椅,现从甲、乙两商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为50元.甲商场称:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌椅均按报价的八五折销售.那么,学校应如何购买更优惠?
21.(8分)绿谷商场“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示:
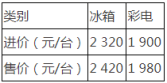
(1)按国家政策,农民购买“家电下乡”产品可享受售价13%的政府补贴.农民田大伯到该商场购买了冰箱、彩电各一台,可以享受多少元的政府补贴?
(2)为满足农民需求,商场决定用不超过85000元采购冰箱、彩电共40台,且冰箱的数量不少于彩电数量的![]() .
.
①请你帮助该商场设计相应的进货方案;
②哪种进货方案商场获得利润最大(利润=售价-进价),最大利润是多少?
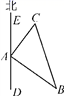
22.(10分)如图,甲、乙两船从港口A同时出发,甲船以30海里/时的速度向北偏东35°的方向航行,乙船以40海里/时的速度向另一方向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,则乙船航行的方向是南偏东多少度?
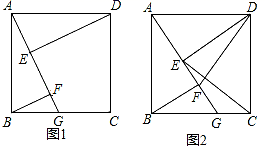
23.(10分)如图1,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)求证:DE=AF;
(2)若AB=4,BG=3,求AF的长;
(3)如图2,连接DF、CE,判断线段DF与CE的位置关系并证明.
24.(12分)化简:
(1)2ab﹣a2+(a﹣b)2
(2)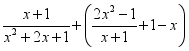
参考答案
一、选择题(每小题3分,共30分)
1、C
2、A
3、D
4、C
5、D
6、C
7、C
8、B
9、B
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、![]() 或
或![]()
13、![]()
14、AB=2BC.
15、x≥-3
16、0.1
三、解下列各题(本大题共8小题,共72分)
17、(1)1;(2)![]() .
.
18、详见解析
19、(1)①![]() ,②平行四边形;(2)结论①不变,结论②由平行四边形变为菱形,理由详见解析;(3)
,②平行四边形;(2)结论①不变,结论②由平行四边形变为菱形,理由详见解析;(3)![]()
20、当购买的餐椅大于等于9少于32把时,到甲商场购买更优惠.
21、(1)572元;(2)①见解析;②3620元.
22、乙船航行的方向为南偏东55°.
23、(1)证明见解析;(2)![]() ;(3)DF⊥CE;证明见解析.
;(3)DF⊥CE;证明见解析.
24、(1)b2;(2)![]() .
.
河北省保定市雄县2022-2023学年八年级下学期期末数学试题: 这是一份河北省保定市雄县2022-2023学年八年级下学期期末数学试题,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
河北省保定市雄县2022-2023学年八年级下学期期末数学试题(含答案): 这是一份河北省保定市雄县2022-2023学年八年级下学期期末数学试题(含答案),共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
河北省保定市雄县2022-2023学年七年级下学期期末数学试题(含答案): 这是一份河北省保定市雄县2022-2023学年七年级下学期期末数学试题(含答案),共9页。试卷主要包含了答案须用黑色字迹的签字笔书写,解以下两个方程组,已知,则下列不等式错误的是,已知,则的值是,下列命题正确的是等内容,欢迎下载使用。












