2022-2023学年江西省抚州市临川区第四中学七年级数学第二学期期末联考试题含答案

2022-2023学年江西省抚州市临川区第四中学七年级数学第二学期期末联考试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．随机抽取10名八年级同学调查每天使用零花钱的情况，结果如下表，则这10名同学每天使用零花钱的中位数是（  ）

A．2元 B．3元 C．4元 D．5元

2．如图，的中线、交于点，连接，点、分别为、的中点，，，则四边形的周长为（    ）

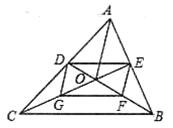
A．12 B．14 C．16 D．18

3．如图，在菱形ABCD中，对角线AC，BD相交于点O. 下列结论中不一定成立的是（   ）

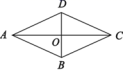
A．AB∥CD B．OA=OC

C．AC⊥BD D．AC=BD

4．下列调查中，适合普查的事件是（　）

A．调查华为手机的使用寿命v

B．调查市九年级学生的心理健康情况

C．调查你班学生打网络游戏的情况

D．调查中央电视台《中国舆论场》的节目收视率

5．如图，在正方形OABC中，点A的坐标是（﹣3，1），点B的纵坐标是4，则B，C两点的坐标分别是（　　）

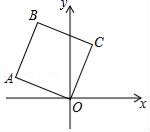
A．（﹣2，4），（1，3） B．（﹣2，4），（2，3）

C．（﹣3，4），（1，4） D．（﹣3，4），（1，3）

6．下列数中不是有理数的是（　　）

A．﹣3.14 B．0 C． D．π

7．如图，已知一次函数y=kx+b（k，b为常数，且k≠0）的图象与x轴交于点A（3，0），若正比例函数y=mx（m为常数，且m≠0）的图象与一次函数的图象相交于点P，且点P的横坐标为1，则关于x的不等式（k-m）x+b＜0的解集为（　　）

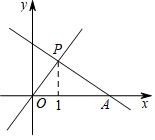
A． B． C． D．

8．如图，正方形的对角线是菱形的一边，则等于（ ）

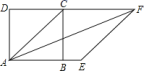
A．135° B．45° C．22.5° D．30°

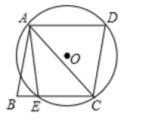
9．如图，四边形ABCD是菱形，圆O经过点A、C、D，与BC相交于点E，连接AC、AE．若，则（    ）

A． B． C． D．

10．定义新运算“”如下：当时，；当时，，若，则的取值范围是（      ）

A．或 B．或

C．或 D．或

11．甲，乙两个样本的容量相同，甲样本的方差为0.102，乙样本的方差是0.06，那么（ ）

A．甲的波动比乙的波动大 B．乙的波动比甲的波动大

C．甲，乙的波动大小一样 D．甲，乙的波动大小无法确定

12．观察下列一组数：1，1，，，，，______。按照这组数的规律横线上的数是（    ）

A． B． C． D．

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．方程的解是________.

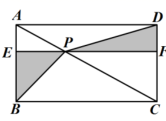
14．如图，在矩形中，点在对角线上，过点作，分别交，于点，，连结，.若，，图中阴影部分的面积为，则矩形的周长为_______.

15．甲、乙、丙、丁四人进行射击测试，每人10次射击成绩平均数均是9.2环，方差分别为，，，，则成绩最稳定的是______．

16．已知1＜x＜5，化简+|x-5|=____．

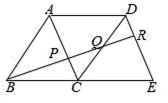
17．如图将△ABC沿BC平移得△DCE，连AD,R是DE上的一点，且DR：RE＝1：2,BR分别与AC,CD相交于点P,Q，则BP：PQ：QR＝__．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）数学活动课上，老师提出了一个问题：如图1，A、B两点被池塘隔开，在AB外选一点，连接AC和BC，怎样测出A、B两点的距离？

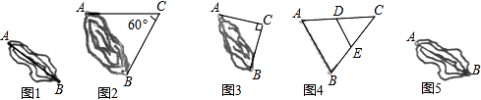
（活动探究）学生以小组展开讨论，总结出以下方法：

⑴如图2，选取点C，使AC=BC=a，∠C=60°；

⑵如图3，选取点C，使AC=BC=b，∠C=90°；

⑶如图4，选取点C，连接AC，BC，然后取AC、BC的中点D、E，量得DE=c…

（活动总结）

（1）请根据上述三种方法，依次写出A、B两点的距离．（用含字母的代数式表示）并写出方法⑶所根据的定理．AB=________，AB=________，AB=________．定理：________．

（2）请你再设计一种测量方法，（图5）画出图形，简要说明过程及结果即可．

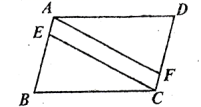
19．（5分）如图，在中，点、分别是、上的点，且.求证：四边形是平行四边形.

20．（8分）计算：，

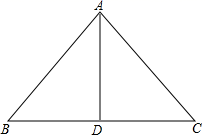
21．（10分）在△ABC中，AB＝AC＝10，D为BC边上的中点，BD＝6，连接AD．

（1）尺规作图：作AC边的中垂线交AD于点P；（保留作图痕迹，不要求写作法和证明）

（2）连接CP，求△DPC的周长．

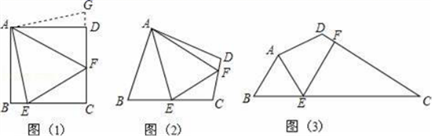
22．（10分）问题：如图(1)，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．

（发现证明）小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图（1）证明上述结论．

（类比引申）如图(2)，四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足                      关系时，仍有EF=BE+FD．

（探究应用）如图(3)，在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据：=1.41，=1.73）

23．（12分）近年，教育部多次明确表示，今后中小学生参加体育活动情况、学生体质健康状况和运动技能等级纳入初中、高中学业水平考试，纳入学生综合素质评价体系．为更好掌握学生体育水平，制定合适的学生体育课内容，某初级中学对本校初一，初二两个年级的学生进行了体育水平检测．为了解情况，现从两个年级抽样调查了部分学生的检测成绩，过程如下：

（收集数据）从初一、初二年级分别随机抽取了20名学生的水平检测分数，数据如下：

（整理数据）按如下分段整理样本数据：

（分析数据）对样本数据边行如下统计：

（得出结论）

（1）根据统计，表格中a、b、c、d的值分别是　   　、　   　、　   　、　   　．

（2）若该校初一、初二年级的学生人数分别为800人和1000人，则估计在这次考试中，初一、初二成绩90分以上（含90分）的人数共有　   　人．

（3）根据以上数据，你认为　   　（填“初一“或“初二”）学生的体育整体水平较高．请说明理由（一条理由即可）．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、B

2、B

3、D

4、C

5、A

6、D

7、B

8、C

9、B

10、D

11、A

12、B

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、

14、

15、甲

16、4

17、2：1：1

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、见解析

19、见解析.

20、5-2

21、（1）见解析；（2）1

22、

23、（1）3、6、84.5、85；（2）490；（3） “初二”，理由详见解析．