


2022-2023学年广东省茂名市茂南区数学七下期末经典试题含答案
展开2022-2023学年广东省茂名市茂南区数学七下期末经典试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.宇宙船使用的陀螺仪直径要求误差不能超过0.00000012米.用科学记数法表示为( )
A.1.2×10﹣7米 B.1.2×107米 C.1.2×10﹣6米 D.1.2×106米
2.如图是一张直角三角形的纸片,两直角边AC=6 cm、BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )

A.4 cm B.5 cm C.6 cm D.10 cm
3.将一副三角尺按如图的方式摆放,其中l1∥l2,则∠α的度数是( )

A.30° B.45° C.60° D.70°
4.若一个多边形的内角和是外角和的3倍,则这个正多边形的边数是( )
A.10 B.9 C.8 D.6
5.平行四边形![]() 中,若
中,若![]() ,则
,则![]() 的度数为( ).
的度数为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.下列交通标志图案中,是中心对称图形的是( )
A. B.
B. C.
C. D.
D.
7.如图,李老师骑自行车上班,最初以某一速度匀速行进,路途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校.在课堂上,李老师请学生画出他行进的路程y(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是( )
A.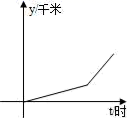 B.
B.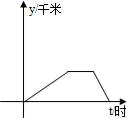
C.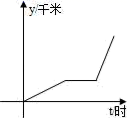 D.
D.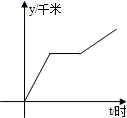
8.下列图形中,是中心对称图形但不是轴对称图形的是( )
A. B.
B. C.
C. D.
D.
9.如果![]() ,那么下列各式一定不成立的是( )
,那么下列各式一定不成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.对于反比例函数![]() ,当
,当![]() 时,y的取值范围是( )
时,y的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.下列图形中既是轴对称图形又是中心对称图形的是( )
A.等腰三角形 B.平行四边形 C.正五边形 D.正十边形
12.为参加学校举办的“诗意校园•致远方”朗诵艺术大赛,八年级“屈原读书社”组织了五次选拔赛,这五次选拔赛中,小明五次成绩的平均数是90,方差是2;小强五次成绩的平均数也是90,方差是14.1.下列说法正确的是( )
A.小明的成绩比小强稳定
B.小明、小强两人成绩一样稳定
C.小强的成绩比小明稳定
D.无法确定小明、小强的成绩谁更稳定
二、填空题(每题4分,满分20分,将答案填在答题纸上)
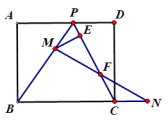
13.如图,在矩形ABCD中,AD=10,AB=8,点P在AD上,且BP=BC,点M在线段BP上,点N在线段BC的延长线上,且MP=NC,连接MN交线段PC于点F,过点M作ME⊥PC于点E,则EF= _______.
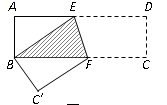
14.如图,在矩形ABCD中,AD=9cm,AB=3cm,将其折叠,使点D与点B重合,则重叠部分(△BEF)的面积为_________cm2.
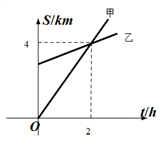
15.已知A地在B地的正南方3km处,甲、乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(km)与所行时间t(h)之间的函数关系如图所示,当他们行驶3h时,他们之间的距离为______km.
16.在函数y=![]() 中,自变量x的取值范围是____.
中,自变量x的取值范围是____.
17.甲、乙两人进行射击测试,每人10次射击的平均成绩恰好都是9.5环,方差分别是S甲2=0.90平方环,S乙2=1.22平方环,在本次射击测试中,甲、乙两人中成绩较稳定的是__.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)某校八年级甲,乙两班各有![]() 名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取
名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取![]() 名学生进行身体素质测试,测试成绩如下:
名学生进行身体素质测试,测试成绩如下:
甲班![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
乙班![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
整理上面数据,得到如下统计表:

样本数据的平均数、众数.中位数如下表所示:
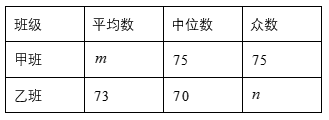
根据以上信息,解答下列问题:
(1)求表中![]() 的值
的值
(2)表中![]() 的值为( )
的值为( )
(3)若规定测试成绩在![]() 分以上(含
分以上(含![]() 分)的学生身体素质为优秀,请估计乙班
分)的学生身体素质为优秀,请估计乙班![]() 名学生中身体素质为优秀的学生的人数.
名学生中身体素质为优秀的学生的人数.
19.(5分)某公司欲招聘一名工作人员,对甲、乙两位应聘者进行面试和笔试,他们的成绩(百分制)如下表所示:
应聘者 | 面试 | 笔试 |
甲 | 87 | 90 |
乙 | 91 | 82 |
若公司分别赋予面试成绩和笔试成绩6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
20.(8分)如图,在平行四边形ABCD中,点E、F在对角线BD上,且BF=DE
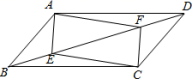
(1)求证:△ADE≌△CBF.
(2)若AE=3,AD=4,∠DAE=90°,该判断当BE的长度为多少时,四边形AECF为菱形,并说明理由.
21.(10分)某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.
(1)若小明获得1次抽奖机会,小明中奖是 事件;(填随机、必然、不可能)
(2)小明观察一段时间后发现,平均每8个人中会有1人抽中一等奖,2人抽中二等奖,若袋中共有24个球,请你估算袋中白球的数量;
(3)在(2)的条件下,如果在抽奖袋中减少3个白球,那么抽奖一次恰好抽中一等奖的概率是多少?请说明理由.
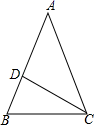
22.(10分)如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为D,CD=1.求AC的长.
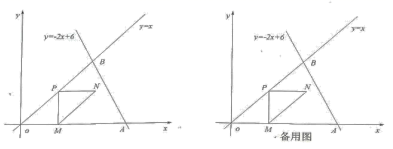
23.(12分)如图,直线y=-2x+6与x轴交于点A,与直线y=x交于点B.
(1)点A坐标为_____________.
(2)动点M从原点O出发,以每秒1个单位长度的速度沿着O→A的路线向终点A匀速运动,过点M作MP⊥x轴交直线y=x于点P,然后以MP为直角边向右作等腰直角△MPN.设运动t秒时,ΔMPN与ΔOAB重叠部分的面积为S.求S与t之间的函数关系式,并直接写出t的取值范围.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、B
3、C
4、C
5、B
6、C
7、C
8、A
9、C
10、A
11、D
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、7.1cm2
15、1.5
16、x≥-2且x≠1
17、甲
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)72;(2)70;(3)20.
19、甲将被录取
20、(1)证明见解析;(2)BE的长度为![]() 时,四边形AECF为菱形.
时,四边形AECF为菱形.
21、(1)必然;(2)15个;(3)![]() ,理由见解析.
,理由见解析.
22、AC=![]()
23、 (1)(3,0);(2)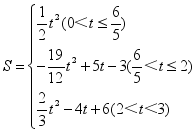
广东省茂名市茂南区2023-2024学年数学八上期末监测模拟试题含答案: 这是一份广东省茂名市茂南区2023-2024学年数学八上期末监测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
广东省茂名市茂南区2022-2023学年七年级上学期期末考试数学试题: 这是一份广东省茂名市茂南区2022-2023学年七年级上学期期末考试数学试题,共5页。
广东省茂名市茂南区2022-2023学年九年级上学期期末考试数学试题: 这是一份广东省茂名市茂南区2022-2023学年九年级上学期期末考试数学试题,共4页。












