


2022-2023学年山东省泰安宁阳县联考七下数学期末经典试题含答案
展开2022-2023学年山东省泰安宁阳县联考七下数学期末经典试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.点P(-2,3)关于y轴的对称点的坐标是( )
A.(2,3) B.(-2,3) C.(2,-3) D.(-2,-3)
2.设正比例函数![]() 的图象经过点
的图象经过点![]() ,且
,且![]() 的值随x值的增大而减小,则
的值随x值的增大而减小,则![]() ( )
( )
A.2 B.-2 C.4 D.-4
3.下列说法正确的是( )
A.![]() 是二项方程 B.
是二项方程 B.![]() 是二元二次方程
是二元二次方程
C.![]() 是分式方程 D.
是分式方程 D.![]() 是无理方程
是无理方程
4.已知4<m<5,则关于x的不等式组![]() 的整数解共有( )
的整数解共有( )
A.1个 B.2个 C.3个 D.4个
5.如图,已知▱ABCD中,点M是BC的中点,且AM=6,BD=12,AD=4![]() ,则该平行四边形的面积为( )
,则该平行四边形的面积为( )
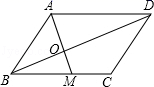
A.24![]() B.36 C.48 D.72
B.36 C.48 D.72
6.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
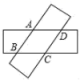
A.5 cm B.4.8 cm C.4.6 cm D.4 cm
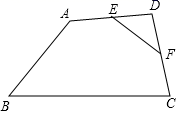
7.如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .若点
.若点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,则
的中点,则![]() 的长是
的长是![]()
![]()
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
8.下列二次根式中,可与![]() 合并的二次根式是
合并的二次根式是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.下表记录了甲、乙、丙、丁四名同学参加某区“中华魂”主题教育演讲比赛的相关数据:根据表中数据,要从中选择一名成绩好且发挥稳定的同学参加市级比赛,应该选择![]()
![]()
| 甲 | 乙 | 丙 | 丁 |
平均数 | 90 | 80 | 90 | 80 |
方差 |
|
|
|
|
A.甲 B.乙 C.丙 D.丁
10.如图,函数![]() (
(![]() )和
)和![]() (
(![]() )的图象相交于点A
)的图象相交于点A![]() ,则不等式
,则不等式![]() >
>![]() 的解集为( )
的解集为( )
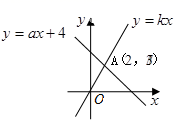
A.![]() >
>![]() B.
B.![]() <
<![]() C.
C.![]() >
>![]() D.
D.![]() <
<![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.一次函数y=2x的图象沿x轴正方向平移3个单位长度,则平移后的图象所对应的函数表达式为_____.
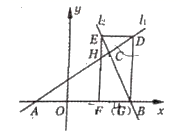
12.如图,已知直线![]() :
:![]() 与直线
与直线![]() :
:![]() 相交于点
相交于点![]() ,直线
,直线![]() 、
、![]() 分别交
分别交![]() 轴于
轴于![]() 、
、![]() 两点,矩形
两点,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,顶点
上,顶点![]() 、
、![]() 都在
都在![]() 轴上,且点
轴上,且点![]() 与
与![]() 点重合,那么
点重合,那么![]() __________________.
__________________.
13.若式子![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.如图,已知矩形![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,在
中点,在![]() 上取一点
上取一点![]() ,使
,使![]() 的面积等于
的面积等于![]() ,则
,则![]() 的长度为_______.
的长度为_______.
15.在![]() 中,若∠A=38°,则∠C=____________
中,若∠A=38°,则∠C=____________
16.菱形的周长为8,它的一个内角为60°,则菱形的较长的对角线长为__________.
三、解下列各题(本大题共8小题,共72分)
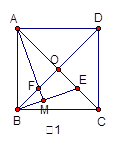
17.(8分)如图l,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM![]() BE,垂足为M,AM交BD于点F.
BE,垂足为M,AM交BD于点F.
(1)求证:OE=OF;
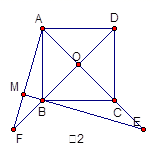
(2)如图2,若点E在AC的延长线上,AM![]() BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗.如果成立,请给出证明;如果不成立,请说明理由.
BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗.如果成立,请给出证明;如果不成立,请说明理由.
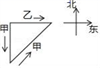
18.(8分)《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的![]() 速度为7,乙的速度为1.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲
速度为7,乙的速度为1.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲![]() 、乙各走了多远?
、乙各走了多远?
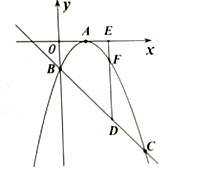
19.(8分)如图,已知二次函数![]() 的图象顶点在
的图象顶点在![]() 轴上,且
轴上,且![]() ,与一次函数
,与一次函数![]() 的图象交于
的图象交于![]() 轴上一点
轴上一点![]() 和另一交点
和另一交点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点
点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交抛物线于点
,交抛物线于点![]() ,请求出线段
,请求出线段![]() 的最大值.
的最大值.
20.(8分)在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
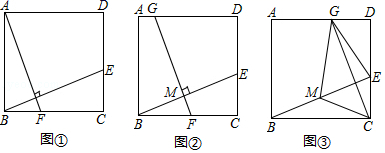
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
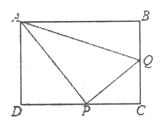
21.(8分)如图,在直角坐标系中,点![]() 为坐标原点,点
为坐标原点,点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,矩形
轴的正半轴上,矩形![]() 的边
的边![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过边
的图象经过边![]() 的中点
的中点![]() .
.
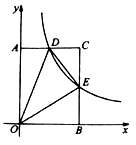
(1)求该反比例函数的表达式;
(2)求![]() 的面积.
的面积.
22.(10分)甲乙两位同学参加数学综合素质测试,各项成绩如下表:(单位:分)
| 数与代数 | 空间与图形 | 统计与概率 | 综合与实践 |
学生甲 | 93 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙同学成绩的中位数;
(2)如果数与代数,空间与图形,统计与概率,综合与实践的成绩按4:3:1:2计算,那么甲、乙同学的数学综合素质成绩分别为多少分?
23.(10分)如图,菱形ABCD的对角线AC和BD相交于点O,AB=![]() ,OA=a,OB=b,且a,b满足:
,OA=a,OB=b,且a,b满足:![]() .
.
(1)求菱形ABCD的面积;
(2)求![]() 的值.
的值.
24.(12分)如图,已知A、B两艘船同时从港口Q出发,船A以40km/h的速度向东航行;船B以30km/h的速度向北航行,它们离开港口2h后相距多远?
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、A
4、B
5、C
6、A
7、C
8、A
9、A
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、y=2x﹣6
12、2:5
13、B
14、![]()
15、38°
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)证明见解析;(2)成立,证明见解析.
18、甲走了24.5步,乙走了10.5步
19、 (1) ![]() ;(2)线段
;(2)线段![]() 的最大值为
的最大值为![]() .
.
20、(1)证明见解析;(1)1,2.
21、(1)![]() ;(2)
;(2)![]() .
.
22、(1)甲的中位数91.5,乙的中位数93;(2)甲的数学综合成绩92,乙的数学综合成绩91.1.
23、(1)4;(2)![]()
24、它们离开港口2h后相距100km.
山东省泰安市宁阳县2023-2024学年八年级数学第一学期期末经典模拟试题含答案: 这是一份山东省泰安市宁阳县2023-2024学年八年级数学第一学期期末经典模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
2023-2024学年山东省泰安宁阳县联考数学八上期末监测模拟试题含答案: 这是一份2023-2024学年山东省泰安宁阳县联考数学八上期末监测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列说法正确的是,下列图形具有稳定性的是,4的算术平方根是等内容,欢迎下载使用。
山东省鄄城县联考2022-2023学年七下数学期末经典模拟试题含答案: 这是一份山东省鄄城县联考2022-2023学年七下数学期末经典模拟试题含答案,共6页。试卷主要包含了多项式与的公因式是,下列变形是因式分解的是等内容,欢迎下载使用。












