山东省鄄城县联考2022-2023学年七下数学期末经典模拟试题含答案

山东省鄄城县联考2022-2023学年七下数学期末经典模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．下列各组数中不能作为直角三角形的三边长的是（　　）

A．，， B．6，8，10 C．7，24，25 D．，3，5

2．等边三角形的边长为2，则该三角形的面积为（　　）

A．4 B． C．2 D．3

3．（2011•潼南县）目前，全球淡水资源日益减少，提倡全社会节约用水．据测试：拧不紧的水龙头每分钟滴出100滴水，每滴水约0.05毫升．小康同学洗手后，没有把水龙头拧紧，水龙头以测试的速度滴水，当小康离开x分钟后，水龙头滴出y毫升的水，请写出y与x之间的函数关系式是（　　）

 A、y=0.05x  B、y=5x

 C、y=100x  D、y=0.05x+100

4．多项式与的公因式是(　　)

A． B． C． D．

5．下列各组数中，不是直角三角形的三条边的长的是（    ）

A．3，4，5 B．6，8，10 C．5，12，13 D．4，5，6

6．点（a，﹣1）在一次函数y＝﹣2x+1的图象上，则a的值为（　　）

A．a＝﹣3 B．a＝﹣1 C．a＝1 D．a＝2

7．如果下列各组数是三角形的三边，则能组成直角三角形的是（      ）

A． B． C． D．

8．下列变形是因式分解的是（　　）

A．x（x+1）＝x2+x B．m2n+2n＝n（m+2）

C．x2+x+1＝x（x+1）+1 D．x2+2x﹣3＝（x﹣1）（x+3）

9．下列命题，①4的平方根是2；②有两边和一角相等的两个三角形全等；③等腰三角形的底角必为锐角；④两组对角分别相等的四边形是平行四边形.其中真命题有(   )

A．4个 B．3个 C．2个 D．1个

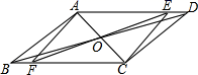
10．如图，平行四边形ABCD对角线AC、BD交于点O，∠ADB=20°，∠ACB=50°，过点O的直线交AD于点E，交BC于点F当点E从点A向点D移动过程中（点E与点A、点D不重合），四边形AFCE的形状变化依次是（　　）

A．平行四边形→矩形→平行四边形→菱形→平行四边形

B．平行四边形→矩形→平行四边形→正方形→平行四边形

C．平行四边形→菱形→平行四边形→矩形→平行四边形

D．平行四边形→矩形→菱形→正方形→平行四边形

11．一次函数的图像与y轴交点的坐标是（   ）

A．（0，-4） B．（0，4） C．（2，0） D．（-2，0）

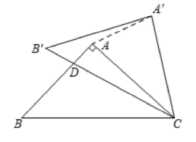
12．如图，中，，，将绕点顺时针旋转得到出，与相交于点，连接，则的度数为（   ）

A． B． C． D．

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如果点P（m+3，m+1）在x轴上，则点P的坐标为________

14．当1≤x≤5时，

15．若分式的值为零，则__________.

16．在一次捐款活动中，某班第一小组8名同学捐款的金额单位：元如下表所示：这8名同学捐款的平均金额为______元

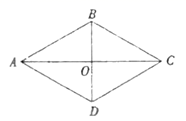
17．如图，菱形ABCD的周长是20，对角线AC、BD相交于点O.若BO=3，则菱形ABCD的面积为______.

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）目前节能灯在城市已基本普及，今年山东省面向县级及农村地区推广,为响应号召，某商场计划购进甲，乙两种节能灯共只，这两种节能灯的进价、售价如下表:

 (1)如何进货，进货款恰好为元?

(2)设商场购进甲种节能灯只，求出商场销售完节能灯时总利润与购进甲种节能灯之间的函数关系式;

(3)如何进货，商场销售完节能灯时获利最多且不超过进货价的，此时利润为多少元？

19．（5分）阅读下列材料并解答问题：

数学中有很多恒等式可以用图形的面积来得到例如，图1中阴影部分的面积可表示为；若将阴影部分剪下来，重新拼成一个矩形如图，它的长，宽分别是，，由图1，图2中阴影部分的面积相等，可得恒等式．

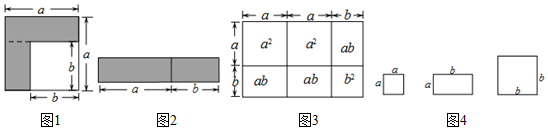
（1）观察图3，根据图形，写出一个代数恒等式：______；

（2）现有若干块长方形和正方形硬纸片如图4所示请你仿照图3，用拼图的方法推出恒等式，画出你的拼图并标出相关数据；

（3）利用前面推出的恒等式和计算：

①；

②．

20．（8分）如图1，在正方形ABCD中，E，F分别是AD，CD上两点，BE交AF于点G，且DE＝CF．

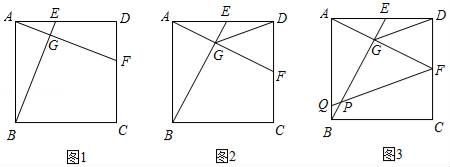
（1）写出BE与AF之间的关系，并证明你的结论；

（2）如图2，若AB＝2，点E为AD的中点，连接GD，试证明GD是∠EGF的角平分线，并求出GD的长；

（3）如图3，在（2）的条件下，作FQ∥DG交AB于点Q，请直接写出FQ的长．

21．（10分）如图，平面直角坐标系中，已知点，若对于平面内一点C，当是以AB为腰的等腰三角形时，称点C时线段AB的“等长点”．

请判断点，点是否是线段AB的“等长点”，并说明理由；

若点是线段AB的“等长点”，且，求m和n的值．

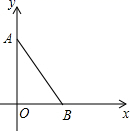
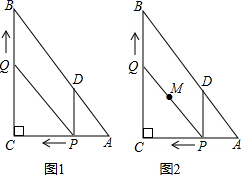
22．（10分）如图1，在中，，，，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作，交AB于点D，连接PQ，点P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒．

直接用含t的代数式分别表示：______，______；

是否存在t的值，使四边形PDBQ为平行四边形？若存在，求出t的值；若不存在，说明理由．

如图2，在整个运动过程中，求出线段PQ中点M所经过的路径长．

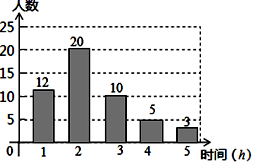
23．（12分）珠海市某中学在创建“书香校园”活动中，为了解学生的读书情况，某校抽样调查了部分同学在一周内的阅读时间，绘制如下统计图．根据图中信息，解答下列问题：

（1）被抽查学生阅读时间的中位数为　   　h，平均数为　   　h；

（2）若该校共有1500名学生，请你估算该校一周内阅读时间不少于3h的学生人数．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、A

2、B

3、：解：y=100×0.05x，

即y=5x．

故选B．

4、B

5、D

6、C

7、A

8、D

9、C

10、C

11、B

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、（2，0）

14、1．

15、-1

16、6.5

17、24

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）乙型节能灯为800； （2）； （3）购进乙型节能灯只时的最大利润为元.

19、（1）；（2）；（3）①1；②．

20、（1）BE＝AF，BE⊥AF;（2）GD是∠EGF的角平分线，证明见解析，GD＝；（3）FQ＝.

21、是线段AB的“等长点”，不是线段AB的“等长点”，理由见解析；，或，．

22、（1），；（2）详见解析；（3）2

23、（1）2h,2.34h;(2)540.