


2023年人教版九年级上册第22章《二次函数》章末测试卷
展开
这是一份2023年人教版九年级上册第22章《二次函数》章末测试卷,共6页。
2023年人教版九年级上册第22章《二次函数》章末测试卷一、选择题(共30分)1.下列函数中,属于二次函数的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.抛物线
2.抛物线![]() 的顶点坐标是( )A.
的顶点坐标是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.已知二次函数
3.已知二次函数![]() ,当函数值
,当函数值![]() 随
随![]() 值的增大而减小时,
值的增大而减小时,![]() 的取值范围是( )A.
的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.函数
4.函数![]() 与
与![]() 在同一直角坐标系中的大致图象可能是( )A.
在同一直角坐标系中的大致图象可能是( )A.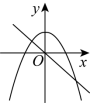 B.
B.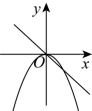 C.
C.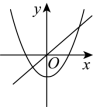 D.
D.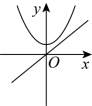 5.关于抛物线
5.关于抛物线![]() ,下列说法错误的是( )A.对称轴是直线
,下列说法错误的是( )A.对称轴是直线![]() B.最大值为
B.最大值为![]() C.当
C.当![]() 时,
时,![]() 随
随![]() 的增大而减小 D.与
的增大而减小 D.与![]() 轴只有一个交点6.已知点
轴只有一个交点6.已知点![]() ,
,![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,则
的图象上,则![]() ,
,![]() ,
,![]() 的大小关系是( )A.
的大小关系是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.与抛物线
7.与抛物线![]() 关于x轴对称的抛物线的解析式表示为( )A.
关于x轴对称的抛物线的解析式表示为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.下面的表格列出了函数
8.下面的表格列出了函数![]() (
(![]() 、
、![]() 、
、![]() 是常数,且
是常数,且![]() )的
)的![]() 与
与![]() 的部分对应值,那么方程
的部分对应值,那么方程![]() 的一个根
的一个根![]() 的取值范围是( )
的取值范围是( )![]() …6.176.186.196.20…
…6.176.186.196.20…![]() …
…![]()
![]() 0.020.04…A.
0.020.04…A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.二次函数
9.二次函数![]() 的图象如图所示,对称轴为直线
的图象如图所示,对称轴为直线![]() ,给出下列结论:①
,给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论有( )
,其中正确的结论有( )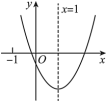 A.1个 B.2个 C.3个 D.4个10.如图,在正方形
A.1个 B.2个 C.3个 D.4个10.如图,在正方形![]() 中,
中,![]() ,动点M,N分别从点A,B同时出发,沿射线
,动点M,N分别从点A,B同时出发,沿射线![]() ,射线
,射线![]() 的方向匀速运动,且速度的大小相等,连接
的方向匀速运动,且速度的大小相等,连接![]() ,
,![]() ,
,![]() .设点M运动的路程为
.设点M运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,下列图像中能反映
,下列图像中能反映![]() 与
与![]() 之间函数关系的是( )
之间函数关系的是( )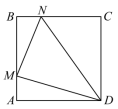 A.
A.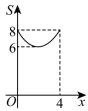 B.
B.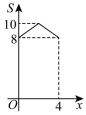 C.
C.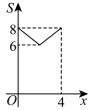 D.
D.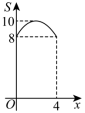 二、填空题(共24分)11.已知函数
二、填空题(共24分)11.已知函数![]() 是二次函数,则
是二次函数,则![]() .12.抛物线
.12.抛物线![]() 的开口方向 .(“向上”或“向下”)13.二次函数
的开口方向 .(“向上”或“向下”)13.二次函数![]() 中,当
中,当![]() 时,y的值是 .14.已知二次函数
时,y的值是 .14.已知二次函数![]() 的图象经过原点,则
的图象经过原点,则![]() 的值为 .15.若抛物线
的值为 .15.若抛物线![]() 与x轴有交点,则k的取值范围是 .16.将二次函数
与x轴有交点,则k的取值范围是 .16.将二次函数![]() 向左平移3个单位长度,再向上平移3个单位长度后,所得抛物线的解析式为 17.一个小球在空中飞行时,飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系式为
向左平移3个单位长度,再向上平移3个单位长度后,所得抛物线的解析式为 17.一个小球在空中飞行时,飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系式为![]() ,则小球从飞出到落地要用的时间为 s.18.如下图,抛物线
,则小球从飞出到落地要用的时间为 s.18.如下图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() 是抛物线上的动点,若
是抛物线上的动点,若![]() 的面积为5,则点
的面积为5,则点![]() 的坐标为 .
的坐标为 .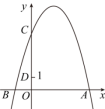 三、解答题(共66分)19.(6分)定义:如果函数图象上存在横、纵坐标相等的点,则称该点为函数的不动点.例如,点
三、解答题(共66分)19.(6分)定义:如果函数图象上存在横、纵坐标相等的点,则称该点为函数的不动点.例如,点![]() 是函数
是函数![]() 的不动点.已知二次函数
的不动点.已知二次函数![]() (
(![]() 是实数).(1)若点
是实数).(1)若点![]() 是该二次函数的一个不动点,求
是该二次函数的一个不动点,求![]() 的值;(2)若该二次函数始终存在不动点,求
的值;(2)若该二次函数始终存在不动点,求![]() 的取值范围. 20.(6分)已知二次函数
的取值范围. 20.(6分)已知二次函数![]() (
(![]() 为常数).(1)求证:不论
为常数).(1)求证:不论![]() 为何值,该函数图象与
为何值,该函数图象与![]() 轴总有两个公共点;(2)当
轴总有两个公共点;(2)当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值. 21.(6分)已知二次函数
的值. 21.(6分)已知二次函数![]() ,解答下列问题:
,解答下列问题: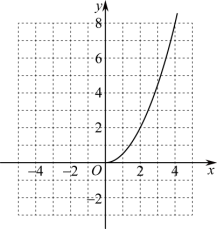 (1)根据已知的图像部分画出这个函数图象的另一部分(直接在网格中作图即可).(2)判断点
(1)根据已知的图像部分画出这个函数图象的另一部分(直接在网格中作图即可).(2)判断点![]() 是否在这个函数图象上,说明理由.(3)求当
是否在这个函数图象上,说明理由.(3)求当![]() 时对应的函数图象上的点的坐标. 22.(8分)如图,抛物线的顶点为C(1,9),与x轴交于A,B(4,0)两点.
时对应的函数图象上的点的坐标. 22.(8分)如图,抛物线的顶点为C(1,9),与x轴交于A,B(4,0)两点.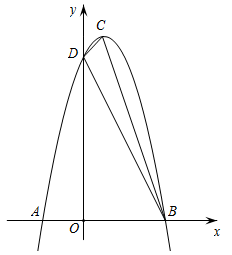 (1)求抛物线的解析式;(2)抛物线与
(1)求抛物线的解析式;(2)抛物线与![]() 轴交点为
轴交点为![]() ,求
,求![]() . 23.(8分)如图,抛物线
. 23.(8分)如图,抛物线![]() 与x轴交
与x轴交![]() 两点(A点在B点左侧),直线
两点(A点在B点左侧),直线![]() 与抛物线交于
与抛物线交于![]() 两点,其中C点的横坐标为
两点,其中C点的横坐标为![]() .
.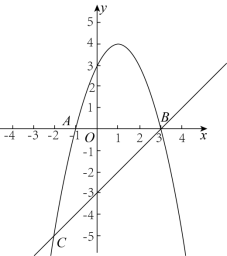 (1)求
(1)求![]() 两点的坐标;(2)求直线
两点的坐标;(2)求直线![]() 的函数表达式;(3)若P是线段
的函数表达式;(3)若P是线段![]() 上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段
上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段![]() 长度的最大值. 24.(10分)
长度的最大值. 24.(10分)![]() 年
年![]() 月
月![]() 日至
日至![]() 日,第
日,第![]() 届冬奥会在北京和张家口举办,这是中国历史上第一次举办冬奥会,吉祥物“冰墩墩”深受大家的喜爱.某超市在今年1月份销售“冰墩墩”
届冬奥会在北京和张家口举办,这是中国历史上第一次举办冬奥会,吉祥物“冰墩墩”深受大家的喜爱.某超市在今年1月份销售“冰墩墩”![]() 个,“冰墩墩”十分畅销,
个,“冰墩墩”十分畅销,![]() 、
、![]() 月份销售量持续走高,在售价不变的基础上,
月份销售量持续走高,在售价不变的基础上,![]() 月份的销售量达到
月份的销售量达到![]() 个.(1)求“冰墩墩”
个.(1)求“冰墩墩”![]() 、
、![]() 这两个月销售量的月平均增长率;(2)若“冰墩墩”每个进价
这两个月销售量的月平均增长率;(2)若“冰墩墩”每个进价![]() 元,原售价为每个
元,原售价为每个![]() 元,该超市在今年
元,该超市在今年![]() 月份进行降价促销,经调查发现,若“冰墩墩”在
月份进行降价促销,经调查发现,若“冰墩墩”在![]() 月份的基础上每个降价
月份的基础上每个降价![]() 元,销售量可增加
元,销售量可增加![]() 个,当“冰墩墩”每个售价为多少元时,出售“冰墩墩”在
个,当“冰墩墩”每个售价为多少元时,出售“冰墩墩”在![]() 月份利润最大,最大利润为多少元? 25.(10分)某公司为城市广场上一雕塑
月份利润最大,最大利润为多少元? 25.(10分)某公司为城市广场上一雕塑![]() 安装喷水装置.喷水口位于雕塑的顶端点B处,距离地面
安装喷水装置.喷水口位于雕塑的顶端点B处,距离地面![]() ,喷出的水柱轨迹呈抛物线型.据此建立如图的平面直角坐标系.若喷出的水柱轨迹
,喷出的水柱轨迹呈抛物线型.据此建立如图的平面直角坐标系.若喷出的水柱轨迹![]() 上,任意一点与支柱
上,任意一点与支柱![]() 的水平距离x(单位:
的水平距离x(单位:![]() )与广场地面的垂直高度为y(单位:
)与广场地面的垂直高度为y(单位:![]() )满足关系式
)满足关系式![]() ,且点
,且点![]() 在抛物线
在抛物线![]() 上
上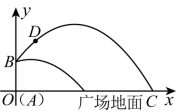 (1)求该抛物线的表达式;(2)求水柱落地点与雕塑
(1)求该抛物线的表达式;(2)求水柱落地点与雕塑![]() 的水平距离;(3)为实现动态喷水效果,广场管理处决定对喷水设施做如下设计改进:新喷水轨迹形成的抛物线形为
的水平距离;(3)为实现动态喷水效果,广场管理处决定对喷水设施做如下设计改进:新喷水轨迹形成的抛物线形为![]() ,把水柱喷水的半径(动态喷水时,点C到
,把水柱喷水的半径(动态喷水时,点C到![]() 的距离)控制在7
的距离)控制在7![]() 到14
到14![]() 之间,请探究改建后喷水池水柱的最大高度 26.(12分)在平面直角坐标系
之间,请探究改建后喷水池水柱的最大高度 26.(12分)在平面直角坐标系![]() 内,抛物线
内,抛物线![]() 交y轴于点C,过点C作x轴的平行线交该抛物线于点D.
交y轴于点C,过点C作x轴的平行线交该抛物线于点D.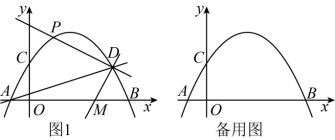 (1)求点C,D的坐标;(2)当
(1)求点C,D的坐标;(2)当![]() 时,如图1,该抛物线与x轴交于A,B两点(点A在点B的左侧),点P为直线
时,如图1,该抛物线与x轴交于A,B两点(点A在点B的左侧),点P为直线![]() 上方抛物线上一点,将直线
上方抛物线上一点,将直线![]() 沿直线
沿直线![]() 翻折,交x轴于点
翻折,交x轴于点![]() ,求点P的坐标;(3)坐标平面内有两点
,求点P的坐标;(3)坐标平面内有两点![]() ,以线段
,以线段![]() 为边向上作正方形
为边向上作正方形![]() .①若
.①若![]() ,求正方形
,求正方形![]() 的边与抛物线的所有交点坐标;②当正方形
的边与抛物线的所有交点坐标;②当正方形![]() 的边与该抛物线有且仅有两个交点,且这两个交点到x轴的距离之差为
的边与该抛物线有且仅有两个交点,且这两个交点到x轴的距离之差为![]() 时,求a的值.
时,求a的值.






