

2022-2023学年山东省日照市七年级数学第二学期期末质量跟踪监视模拟试题含答案
展开2022-2023学年山东省日照市七年级数学第二学期期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若分式![]() 有意义,则x应满足的条件是( )
有意义,则x应满足的条件是( )
A.x≠0 B.x=2 C.x>2 D.x≠2
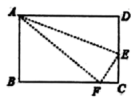
2.如图,在长方形![]() 中,
中,![]() ,在
,在![]() 上存在一点
上存在一点![]() ,沿直线
,沿直线![]() 把
把![]() 折叠,使点
折叠,使点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,若
处,若![]() 的面积为
的面积为![]() ,那么折叠的
,那么折叠的![]() 的面积为( )
的面积为( )![]()
A.30 B.20 C.![]() D.
D.![]()
3.下列各点中,与点(-3,4)在同一个反比例函数图像上的点是
A.(2,-3) B.(3,4) C.(2,-6) D.(-3,-4)
4.下列各式中,运算正确的是( )
A.![]() B.
B.![]()
C.2+![]() =2
=2![]() D.
D.![]()
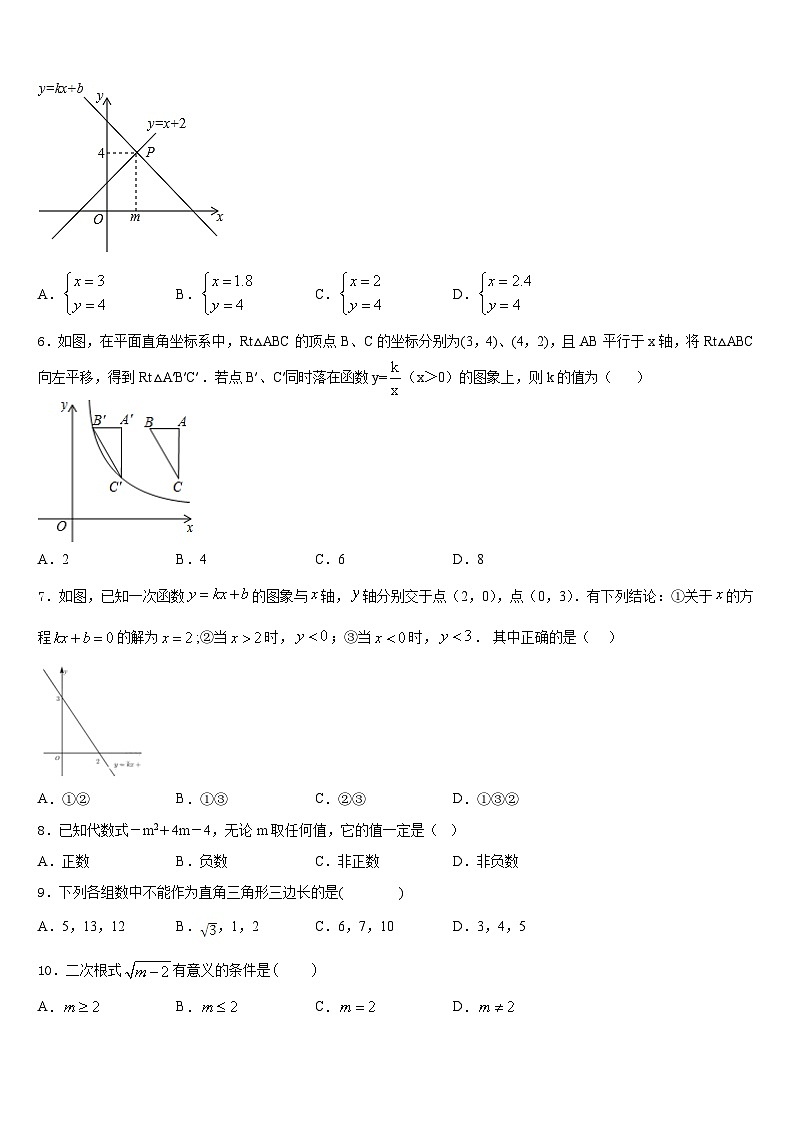
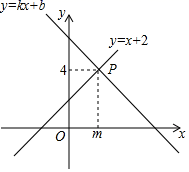
5.如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x,y的二元一次方程组![]() 的解是( )
的解是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
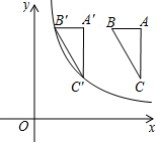
6.如图,在平面直角坐标系中,Rt△ABC的顶点B、C的坐标分别为(3,4)、(4,2),且AB平行于x轴,将Rt△ABC向左平移,得到Rt△A′B′C′.若点B′、C′同时落在函数y=![]() (x>0)的图象上,则k的值为( )
(x>0)的图象上,则k的值为( )
A.2 B.4 C.6 D.8
7.如图,已知一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴分别交于点(2,0),点(0,3).有下列结论:①关于
轴分别交于点(2,0),点(0,3).有下列结论:①关于![]() 的方程
的方程![]() 的解为
的解为![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() . 其中正确的是( )
. 其中正确的是( )
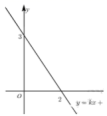
A.①② B.①③ C.②③ D.①③②
8.已知代数式-m2+4m-4,无论m取任何值,它的值一定是( )
A.正数 B.负数 C.非正数 D.非负数
9.下列各组数中不能作为直角三角形三边长的是( )
A.5,13,12 B.![]() ,1,2 C.6,7,10 D.3,4,5
,1,2 C.6,7,10 D.3,4,5
10.二次根式![]() 有意义的条件是
有意义的条件是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.关于![]() 的不等式
的不等式![]() 的解集在数轴上表示如下,则
的解集在数轴上表示如下,则![]() 的取值范围是( )
的取值范围是( )
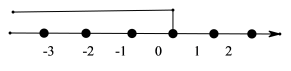
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知正比例函数![]() 的函数值
的函数值![]() 随
随![]() 的增大而减小,则一次函数
的增大而减小,则一次函数![]() 的图象大致是( )
的图象大致是( )
A.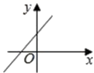 B.
B.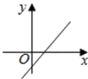 C.
C.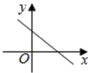 D.
D.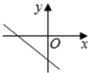
二、填空题(每题4分,满分20分,将答案填在答题纸上)
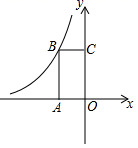
13.如图,点B是反比例函数![]() 在第二象限上的一点,且矩形OABC的面积为4,则k的值为_______________.
在第二象限上的一点,且矩形OABC的面积为4,则k的值为_______________.
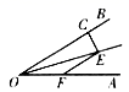
14.如图,点![]() 在
在![]() 的平分线上,
的平分线上,![]() ,垂足为
,垂足为![]() ,点
,点![]() 在
在![]() 上,若
上,若![]() ,则
,则![]() __.
__.
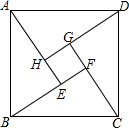
15.如图,在矩形ABCD,BE平分![]() ,交AD于点E,F是BE的中点,G是BC的中点,连按EC,若
,交AD于点E,F是BE的中点,G是BC的中点,连按EC,若![]() ,
,![]() ,则FG的长为________。
,则FG的长为________。
16.一组数据:5,8,7,6,9,则这组数据的方差是_____.
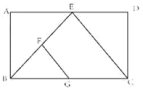
17.勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”.中国是发现和研究勾股定理最古老的国家之一.中国古代数学家称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,所以勾股定理也称为勾股弦定理.三国时期吴国赵爽创制了“勾股圆方图”(如图)证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的.若小正方形的边长是1,每个直角三角形的短的直角边长是3,则大正方形ABCD的面积是_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)某班同学进行数学测验,将所得成绩(得分取整数)进行整理分成五组,并绘制成频数直方图(如图),请结合直方图提供的信息,回答下列问题:
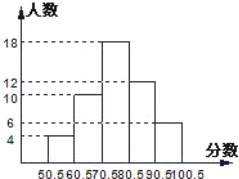
(1)该班共有多少名学生参加这次测验?
(2)求1.5~2.5这一分数段的频数是多少,频率是多少?
(3)若80分以上为优秀,则该班的优秀率是多少?
19.(5分)光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
| 每台甲型收割机的租金 | 每台乙型收割机的租金 |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
20.(8分)如图,P、Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.(顶点都在格点上的四边形称为格点四边形)
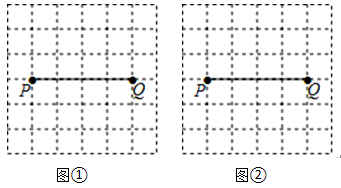
(1)在图①中画出一个面积最小的中心对称图形PAQB,
(2)在图②中画出一个四边形PCQD,使其是轴对称图形但不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.
21.(10分)已知:如图,在四边形![]() 中
中![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,且
,且![]() .
.
求证:四边形![]() 是平行四边形.
是平行四边形.
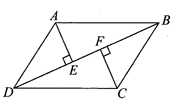
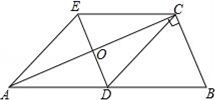
22.(10分)如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
求证:四边形ADCE是菱形.
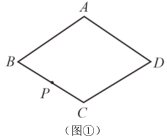
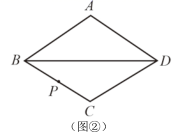
23.(12分)如图,在菱形ABCD中,点P是BC的中点,仅用无刻度的直尺按要求画图. (保
留作图痕迹,不写作法)
(1)在图①中画出AD的中点H;
(2)在图②中的菱形对角线BD上,找两个点E、F,使BE=DF.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、D
3、C
4、A
5、C
6、B
7、A
8、C
9、C
10、A
11、C
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、-1
14、1.
15、5
16、2
17、25
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)50;(2)频数:10 频率:0.2;(3)优秀率:36%
19、(1)y=200x+74000(10≤x≤30)
(2)有三种分配方案,
方案一:派往A地区的甲型联合收割机2台,乙型联合收割机28台,其余的全派往B地区;
方案二:派往A地区的甲型联合收割机1台,乙型联合收割机29台,其余的全派往B地区;
方案三:派往A地区的甲型联合收割机0台,乙型联合收割机30台,其余的全派往B地区;
(3)派往A地区30台乙型联合收割机,20台甲型联合收割机全部派往B地区,使该公司50台收割机每天获得租金最高.
20、(1)画图见解析;(2)画图见解析.
21、证明见解析.
22、证明见解析
23、见解析
山东省日照市莒县2023-2024学年九上数学期末质量跟踪监视试题含答案: 这是一份山东省日照市莒县2023-2024学年九上数学期末质量跟踪监视试题含答案,共8页。试卷主要包含了的值等于,如图,AB是⊙O的弦等内容,欢迎下载使用。
山东省日照市新营中学2023-2024学年八上数学期末质量跟踪监视试题含答案: 这是一份山东省日照市新营中学2023-2024学年八上数学期末质量跟踪监视试题含答案,共6页。
山东省潍坊联考2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案: 这是一份山东省潍坊联考2022-2023学年数学七年级第二学期期末质量跟踪监视模拟试题含答案,共7页。












