


2022-2023学年北京市延庆县名校七年级数学第二学期期末调研试题含答案
展开这是一份2022-2023学年北京市延庆县名校七年级数学第二学期期末调研试题含答案,共7页。
2022-2023学年北京市延庆县名校七年级数学第二学期期末调研试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.如图,点![]() 为
为![]() 的平分线
的平分线![]() 上的一点,
上的一点,![]() 于点
于点![]() .若
.若![]() ,则
,则![]() 到
到![]() 的距离为( )
的距离为( )
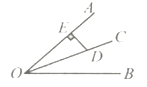
A.5 B.4 C.3.5 D.3
2.在数学活动课上,老师让同学们判定一个四边形门框是否为矩形,下面是某合作小组的四位同学的拟订方案,其中正确的是( )
A.测量对角线是否互相平分
B.测量两组对边是否分别相等
C.测量一组对角是否为直角
D.测量两组对边是否相等,再测量对角线是否相等
3.电视塔越高,从塔顶发射出的电磁波传播得越远,从而能收看到电视节目的区域就越广.电视塔高![]() (单位:
(单位:![]() )与电视节目信号的传播半径
)与电视节目信号的传播半径![]() (单位:
(单位:![]() )之间存在近似关系
)之间存在近似关系![]() ,其中
,其中![]() 是地球半径.如果两个电视塔的高分别是
是地球半径.如果两个电视塔的高分别是![]()
![]() ,
,![]()
![]() ,那么它们的传播半径之比是
,那么它们的传播半径之比是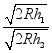 ,则式子
,则式子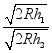 化简为( )
化简为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=2,则矩形的面积为( )
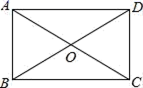
A.2![]() B.4
B.4![]() C.
C.![]() D.3
D.3![]()
5. 小马虎在下面的计算中只作对了一道题,他做对的题目是( )
A.![]() B.a3÷a=a2
B.a3÷a=a2
C.![]() D.
D.![]() =﹣1
=﹣1
6.若等腰![]() 的周长是
的周长是![]() ,一腰长为
,一腰长为![]() ,底边长为
,底边长为![]() ,则
,则![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围是
的取值范围是![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.在中国集邮总公司设计的2017年纪特邮票首日纪念戳图案中,可以看作中心对称图形的是( )
A. B.
B. C.
C. D.
D.
8.下列调查中,适合采用普查的是()
A.了解一批电视机的使用寿命
B.了解全省学生的家庭1周内丢弃塑料袋的数量
C.了解某校八(2)班学生的身高
D.了解淮安市中学生的近视率
9.一次函数y=ax+b与反比例函数![]() ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
A. B.
B.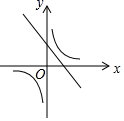 C.
C.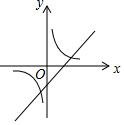 D.
D.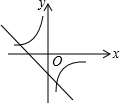
10.如图,等腰梯形 ABCD 的对角线 AC、BD 相交于 O,则图中的全等三 角形有( )
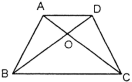
A.1 对 B.2 对 C.3 对 D.4 对
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知▱ABCD的周长为40,如果AB:BC=2:3,那么AB=_____.
12.如图,在平行四边形![]() 中,连接
中,连接![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,在
,在![]() 的延长线上取一点
的延长线上取一点![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的度数为____________
的度数为____________![]() .
.
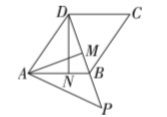
13.如图,矩形![]() 的面积为
的面积为![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于
于![]() ,沿
,沿![]() 将
将![]() 折叠,点
折叠,点![]() 的对应点刚好落在矩形两条对角线的交点
的对应点刚好落在矩形两条对角线的交点![]() 处.则
处.则![]() 的面积为________.
的面积为________.
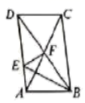
14.命题“全等三角形的面积相等”的逆命题是__________
15.某种药品原来售价100元,连续两次降价后售价为81元,若每次下降的百分率相同,则这个百分率是 .
16.一组数据﹣1,0,1,2,3的方差是_____.
三、解下列各题(本大题共8小题,共72分)
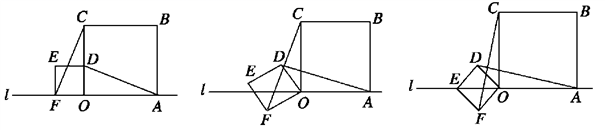
17.(8分)小明在数学活动课上,将边长为![]() 和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针针旋转一定的角度,如图b,试判断AD与CF还相等吗?说明理由.
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图c,请求出CF的长.
![]()
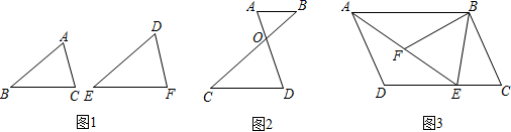
18.(8分)先阅读下面的材料,再解答下面的问题:如果两个三角形的形状相同,则称这两个三角形相似.如图1,△ABC与△DEF形状相同,则称△ABC与△DEF相似,记作△ABC∽△DEF.那么,如何说明两个三角形相似呢?我们可以用“两角分别相等的三角形相似”加以说明.用数学语言表示为:
如图1:在△ABC与△DEF中,∵∠A=∠D,∠B=∠E,∴△ABC∽△DEF.
请你利用上述定理解决下面的问题:
(1)下列说法:①有一个角为50°的两个等腰三角形相似;②有一个角为100°的两个等腰三角形相似;③有一个锐角相等的两个直角三角形相似;④两个等边三角形相似.其中正确的是______(填序号);
(2)如图2,已知AB∥CD,AD与BC相交于点O,试说明△ABO∽△DCO;
(3)如图3,在平行四边形ABCD中,E是DC上一点,连接AE.F为AE上一点,且∠BFE=∠C,求证:△ABF∽△EAD.
19.(8分)某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量净减少10个;定价每减少1元,销售量净增加10个.因受库存的影响,每批次进货个数不得超过180个,商店若将准备获利2000元,则应进货多少个?定价为多少元?
20.(8分)如图,已知过点B(1,0)的直线![]() 与直线
与直线![]() :
:![]() 相交于点P(-1,a).且l1与y轴相交于C点,l2与x轴相交于A点.
相交于点P(-1,a).且l1与y轴相交于C点,l2与x轴相交于A点.
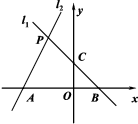
(1)求直线![]() 的解析式;
的解析式;
(2)求四边形![]() 的面积;
的面积;
(3)若点Q是x轴上一动点,连接PQ、CQ,当△QPC周长最小时,求点Q坐标.
21.(8分)已知:如图,在![]() 中,
中,![]() 。
。
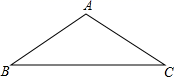
(1)尺规作图:作线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ;(保留作图痕迹,不写作法);
;(保留作图痕迹,不写作法);
(2)求证:![]() 是等腰三角形。
是等腰三角形。
22.(10分)我国南宋时期数学家秦九昭及古希腊的几何学家海伦对于问题:“已知三角形的三边,如何求三角形的面积”进行了研究,并得到了海伦—秦九昭公式:如果一个三角形的三条边分别为![]() ,记
,记![]() ,那么三角形的面积为
,那么三角形的面积为![]() ,请用此公式求解:在
,请用此公式求解:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
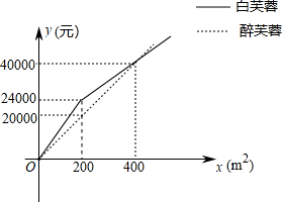
23.(10分)2019车8月8日至18日,第十八届“世警会”首次来到亚洲在成都举办武侯区以相关事宜为契机,进一步改善区域生态环境.在天府吴园道部分地段种植白芙蓉和醉芙蓉两种花卉.经市场调查,种植费用y(元)与种植面积x(m2)之间的函数关系如图所示.
(1)请直接写出两种花卉y与x的函数关系式;
(2)白芙蓉和醉芙蓉两种花卉的种植面积共1000m2,若白芙蓉的种植面积不少于100m2且不超过醉芙蓉种植面积的3倍,那么应该怎样分配两种花卉的种植面积才能使种植总费用最少?
24.(12分)先化简![]() ,然后在0、±1、±2这5个数中选取一个作为x的值代入求值.
,然后在0、±1、±2这5个数中选取一个作为x的值代入求值.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、D
3、D
4、B
5、B
6、C
7、C
8、C
9、C
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1.
12、25
13、![]()
14、如果两个三角形的面积相等,那么是全等三角形
15、10%.
16、1
三、解下列各题(本大题共8小题,共72分)
17、(2)详见解析(2)CF=![]()
18、(1)②③④;(2)见解析;(3)见解析
19、该商品每个定价为1元,进货100个.
20、(1)y=-x+1;(2)![]() ;(3)点Q坐标为(-
;(3)点Q坐标为(-![]() ,0)时△QPC周长最小
,0)时△QPC周长最小
21、(1)见解析;(2)![]() 是等腰三角形,见解析.
是等腰三角形,见解析.
22、![]()
23、(1)y=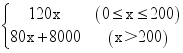 ,y=100x(x≥0);(2)当种植白芙蓉750m2,醉芙蓉250m2时,才能使种植总费用最少
,y=100x(x≥0);(2)当种植白芙蓉750m2,醉芙蓉250m2时,才能使种植总费用最少
24、![]() ,-
,-![]()
相关试卷
这是一份2023-2024学年北京市延庆县名校九年级数学第一学期期末学业质量监测试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,若,面积之比为,则相似比为等内容,欢迎下载使用。
这是一份2023-2024学年北京市延庆县名校数学八年级第一学期期末统考试题含答案,共7页。试卷主要包含了下列运算正确的是,下列计算正确的是,把通分,下列计算正确的是等内容,欢迎下载使用。
这是一份2023-2024学年北京市延庆县八上数学期末达标测试试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,若,则的值是等内容,欢迎下载使用。









