


2022-2023学年北京市崇文区名校数学七下期末调研模拟试题含答案
展开2022-2023学年北京市崇文区名校数学七下期末调研模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.已知一次函数![]() ,若y随着x的增大而增大,且它的图象与y轴交于负半轴,则直线
,若y随着x的增大而增大,且它的图象与y轴交于负半轴,则直线![]() 的大致图象是( )
的大致图象是( )
A.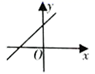 B.
B.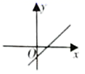 C.
C.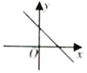 D.
D.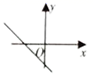
2.小明家、食堂,图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中,小明离家的距离y(km)与时间x(min)之间的对应关系,根据图象,下列说法正确的是( )
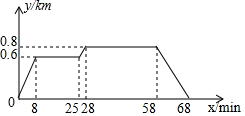
A.小明吃早餐用了25min
B.食堂到图书馆的距离为0.6km
C.小明读报用了30min
D.小明从图书馆回家的速度为0.8km/min
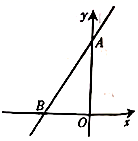
3.如图,直线![]() 过点
过点![]() 和点
和点![]() ,则方程
,则方程![]() 的解是( )
的解是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如图,在▱ABCD中,对角线AC的垂直平分线分别交AD、BC于点E、F,连接CE,若△CED的周长为6,则▱ABCD的周长为( )
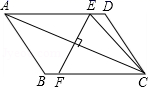
A.6 B.12 C.18 D.24
5.如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=AD,连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:①AH=DF;②∠AEF=45°;③S四边形EFHG=S△DEF+S△AGH;④BH平分∠ABE.其中不正确的结论有( )
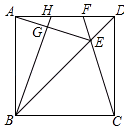
A.1个 B.2个 C.3个 D.4个
6.方程x2 = 2x的解是( )
A.x=2 B.x1=![]() ,x2= 0 C.x1=2,x2=0 D.x = 0
,x2= 0 C.x1=2,x2=0 D.x = 0
7.若代数式![]() 在实数范围内有意义,则a的取值范围是( )
在实数范围内有意义,则a的取值范围是( )
A.a≠0 B.a>2 C.a≥2 D.a≥2且a≠0
8.生物刘老师对本班50名学生的血型进行了统计,列出如下统计表,则本班O型血的有( )
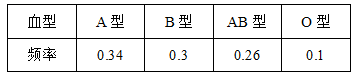
A.17人 B.15人 C.13人 D.5人
9.下列因式分解正确的是( )
A.2x2﹣2=2(x+1)(x﹣1) B.x2+2x﹣1=(x﹣1)2
C.x2﹣1=(x﹣1)2 D.x2﹣x+2=x(x﹣1)+2
10.如图,已知正方形面积为36平方厘米,圆与各边相接,则阴影部分的面积是( )平方厘米.(![]() )
)
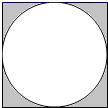
A.18 B.7.74 C.9 D.28.26
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在一个不透明的袋子中有若千个小球,这些球除颜色外无其他差别,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:
摸球实验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
“摸出黑球”的次数 | 36 | 387 | 2019 | 4009 | 19970 | 40008 |
“摸出黑球”的频率 (结果保留小数点后三位) | 0.360 | 0.387 | 0.404 | 0.401 | 0.399 | 0.400 |
根据试验所得数据,估计“摸出黑球”的概率是_______(结果保留小数点后一位).
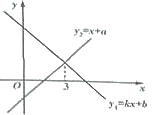
12.已知一次函数![]() 与
与![]() 图象如图所示,则下列结论:①
图象如图所示,则下列结论:①![]() ;②
;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 的解为
的解为![]() ;④当
;④当![]() ,
,![]() .其中正确的有_______(填序号).
.其中正确的有_______(填序号).
13.若a≠b,且a2﹣a=b2﹣b,则a+b=__.
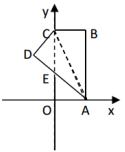
14.如图,在平面直角坐标系中,矩形![]() 的边
的边![]() 在
在![]() 轴上,边
轴上,边![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() .将矩形沿对角线
.将矩形沿对角线![]() 翻折,
翻折,![]() 点落在
点落在![]() 点的位置,且
点的位置,且![]() 交
交![]() 轴于点
轴于点![]() ,那么点
,那么点![]() 的坐标为______.
的坐标为______.
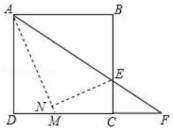
15.如图,正方形ABCD的边长为8,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,则NM的长为_____.
16.某学校八年级![]() 班有
班有![]() 名同学,
名同学,![]() 名男生的平均身高为
名男生的平均身高为![]() 名女生的平均身高
名女生的平均身高![]() ,则全班学生的平均身高是__________
,则全班学生的平均身高是__________![]() .
.
三、解下列各题(本大题共8小题,共72分)
17.(8分)定义:任意两个数![]() ,
,![]() ,按规则
,按规则![]() 得到一个新数
得到一个新数![]() ,称所得的新数
,称所得的新数![]() 为数
为数![]() ,
,![]() 的“传承数.”
的“传承数.”
(1)若![]() ,
,![]() ,求
,求![]() ,
,![]() 的“传承数”
的“传承数”![]() ;
;
(2)若![]() ,
,![]() ,且
,且![]() ,求
,求![]() ,
,![]() 的“传承数”
的“传承数”![]() ;
;
(3)若![]() ,
,![]() ,且
,且![]() ,
,![]() 的“传承数”
的“传承数”![]() 值为一个整数,则整数
值为一个整数,则整数![]() 的值是多少?
的值是多少?
18.(8分)已知一角的两边与另一个角的两边平行,分别结合下图,试探索这两个角之间的关系,并证明你的结论.
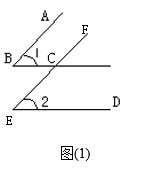
(1)如图(1)AB∥EF,BC∥DE,∠1与∠2的关系是:____________ .
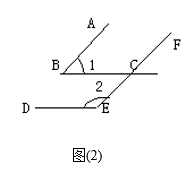
(2)如图(2)AB∥EF,BC∥DE, ∠1与∠2的关系是:____________
(3)经过上述证明,我们可以得到一个真命题:如果____ _____,那么____________.
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角分别是多少度?
19.(8分)已知矩形 ABCD 的一条边 AD=8,将矩形 ABCD 折叠,使得顶点 B 落在 CD 边上的 P 点处.
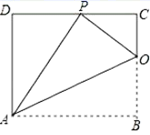
(1)求证:△OCP∽△PDA;
(2)若△OCP 与△PDA 的面积比为 1:4,求边 AB 的长;
20.(8分)先化简,再求值![]() ,其中x=1.
,其中x=1.
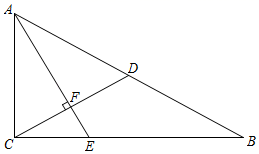
21.(8分)如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD于点F,交CB于点E,且∠EAB=∠DCB.
(1)求∠B的度数:
(2)求证:BC=3CE.
22.(10分)某市米厂接到加工大米任务,要求![]() 天内加工完
天内加工完![]() 大米.米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止,设甲、乙两车间各自加工大米数量
大米.米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止,设甲、乙两车间各自加工大米数量![]() 与甲车间加工时间
与甲车间加工时间![]() (天)之间的关系如图1所示;未加工大米
(天)之间的关系如图1所示;未加工大米![]() 与甲车间加工时间
与甲车间加工时间![]() (天)之间的关系如图2所示,请结合图像回答下列问题
(天)之间的关系如图2所示,请结合图像回答下列问题

(1)甲车间每天加工大米__________;![]() =______________;
=______________;
(2)直接写出乙车间维修设备后,乙车间加工大米数量![]() 与
与![]() (天)之间的函数关系式,并指出自变量的取值范围.
(天)之间的函数关系式,并指出自变量的取值范围.
23.(10分)第二届全国青年运动会将于2019年8月在太原开幕,这是山西历史上第一次举办全国大型综合性运动会,必将推动我市全民健康理念的提高.某体育用品商店近期购进甲、乙两种运动衫各50件,甲种用了2000元,乙种用了2400元.商店将甲种运动衫的销售单价定为60元,乙种运动衫的销售单价定为88元.该店销售一段时间后发现,甲种运动衫的销售不理想,于是将余下的运动衫按照七折销售;而乙种运动衫的销售价格不变.商店售完这两种运动衫至少可获利2460元,求甲种运动衫按原价销售件数的最小值.
24.(12分)如图,在平行四边形ABCD中(AB>AD),AF平分∠DAB,交CD于点F,DE平分∠ADC,交AB于点E,AF与DE交于点O,连接EF
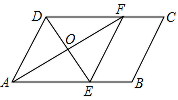
(1)求证:四边形AEFD为菱形;
(2)若AD=2,AB=3,∠DAB=60°,求平行四边形ABCD的面积.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、B
4、B
5、A
6、C
7、C
8、D
9、A
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、0.1
12、③④
13、1.
14、(0,![]() ).
).
15、![]()
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 为-2、0、2或4
为-2、0、2或4
18、(1)∠1=∠1,证明见解析;(1)∠1+∠1=180°,证明见解析;(3)一个角的两边与另一个角的两边分别平行,这两个角相等或互补;(4)这两个角分别是30°,30°或70°,110°.
19、(1)见解析;(2)边AB的长为10.
20、![]() ;
;![]() .
.
21、(1)∠B=30°;(2)详见解析.
22、解:(1)![]() ;
;![]() ; (2)
; (2)![]() ,
,![]()
23、甲种运动衫按原价销售件数的最小值为20 件.
24、(1)见解析;(2)3![]() .
.
北京市崇文区名校2023-2024学年九上数学期末监测模拟试题含答案: 这是一份北京市崇文区名校2023-2024学年九上数学期末监测模拟试题含答案,共7页。试卷主要包含了如图,在中,,,,,则的长为,在中,,若已知,则等内容,欢迎下载使用。
北京市崇文区名校2023-2024学年数学八上期末质量检测模拟试题含答案: 这是一份北京市崇文区名校2023-2024学年数学八上期末质量检测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,下列四组数据,能组成三角形的是,下列关于一次函数,下列各式计算正确的是,已知点在轴的负半轴,则点在等内容,欢迎下载使用。
辽宁省抚顺市名校2022-2023学年数学七下期末调研模拟试题含答案: 这是一份辽宁省抚顺市名校2022-2023学年数学七下期末调研模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,在平行四边形ABCD中,∠A,计算×的结果是等内容,欢迎下载使用。













