2022-2023学年北京市东城区七年级数学第二学期期末联考模拟试题含答案

2022-2023学年北京市东城区七年级数学第二学期期末联考模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

1．满足不等式的正整数是（   ）

A．2.5 B． C．-2 D．5

2．已知▱ABCD的周长为50cm，△ABC的周长为35cm，则对角线AC的长为（　　）

A．5cm B．10cm C．15cm D．20cm

3．方程x(x-2)=0的根是（    ）

A．x=0 B．x=2 C．x1=0，x2=2 D．x1=0，x2=-2

4．将直线向下平移2个单位，得到直线(　　)

A． B． C． D．

5．估计的值在下列哪两个整数之间（    ）

A．6和7之间 B．7和8之间 C．8和9之间 D．无法确定

6．下列等式从左到右的变形，属于因式分解的是（  ）

A． B．

C． D．

7．如图，将平行四边形ABCD折叠，使顶点D恰落在AB边上的点M处，折痕为AN，那么对于结论 ①MN∥BC，②MN=AM，下列说法正确的是（　　）

A．①②都对 B．①②都错

C．①对②错 D．①错②对

8．A、B、C分别表示三个村庄，米，米，米，某社区拟建一个文化活动中心，要求这三个村庄到活动中心的距离相等，则活动中心P的位置应在（  ）

A．AB的中点 B．BC的中点

C．AC的中点 D．的平分线与AB的交点

9．在直角三角形中，两条直角边的长分别为12和5，则斜边上的中线长是（　　）

A．6.5 B．8.5 C．13 D．

10．为测量操场上旗杆的高度，小丽同学想到了物理学中平面镜成像的原理，她拿出随身携带的镜子和卷尺，先将镜子放在脚下的地面上，然后后退，直到她站直身子刚好能从镜子里看到旗杆的顶端E，标记好脚掌中心位置为B，测得脚掌中心位置B到镜面中心C的距离是50cm，镜面中心C距离旗杆底部D的距离为4m，如图所示．已知小丽同学的身高是1.54m，眼睛位置A距离小丽头顶的距离是4cm，则旗杆DE的高度等于（　　）

A．10m    B．12m    C．12.4m    D．12.32m

二、填空题(本大题共有6小题，每小题3分，共18分)

11．甲、乙两人进行射击测试，每人10次射击成绩的平均数均是8.5环，方差分别是：，，则射击成绩较稳定的是______（填“甲”或“乙”）.

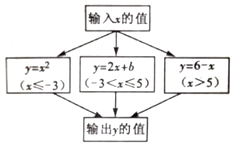
12．根据如图所示的程序计算函数y的值，若输入的x值是4或7时，输出的y值相等，则b等于（________）

13．把直线沿轴向上平移5个单位，则得到的直线的表达式为_________.

14．已知直线y＝x﹣3与y＝2x+2的交点为（﹣5，﹣8），则方程组的解是_____．

15．如图，矩形ABCD的两条对角线相交于点O，若∠AOD＝60°，AD＝2，则AC的长为_____．

16．若代数式在实数范围内有意义，则实数x的取值范围是__________.

三、解下列各题(本大题共8小题，共72分)

17．（8分）计算下列各题：

（1）                 

（2）

18．（8分）在平面直角坐标中，边长为 2 的正方形 OABC 的两顶点 A、C 分别在 y 轴、x 轴的正半轴上，点 O 在原点.现将正方形 OABC 绕 O 点顺时针旋转，当 A 点第一次落在直线 y=x 上时停止旋转，旋转过程中，AB 边交直线 y=x于点 M，BC 边交 x 轴于点 N（如图）.

（1）求边 OA 在旋转过程中所扫过的面积；

（2）旋转过程中，当 MN 和 AC 平行时，求正方形 OABC 旋转的度数；

（3）试证明在旋转过程中, △MNO 的边 MN 上的高为定值；

（4）设△MBN 的周长为 p，在旋转过程中，p 值是否发生变化？若发生变化，说明理由；若不发生变化，请给予证明，并求出 p 的值.

19．（8分）某商场购进甲、乙两种商品，甲种商品共用了2000元，乙种商品共用了2400元已知乙种商品每件进价比甲种商品每件进价多8元，且购进的甲、乙两种商品件数相同．

求甲、乙两种商品的每件进价；

该商场将购进的甲、乙两种商品进行销售，甲种商品的销售单价为60元，乙种商品的销售单价为88元，销售过程中发现甲种商品销量不好，商场决定：甲种商品销售一定数量后，将剩余的甲种商品按原销售单价的七折销售；乙种商品销售单价保持不变要使两种商品全部售完后共获利不少于2460元，问甲种商品按原销售单价至少销售多少件？

20．（8分） (1)计算：(1﹣)÷；

(2)化简求值：(﹣)÷，其中m＝﹣1

21．（8分）随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样、便捷，在一次购物中，张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付．

(1)张华用“微信”支付的概率是______．

(2)请用画树状图或列表法求出两人恰好选择同一种支付方式的概率．(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替)

22．（10分）如图,在四边形ABCD中,AB=AD=3,DC=4,∠A=60°，∠D=150°,试求BC的长度.

23．（10分）（1）如图1，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开；再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN，MN．请你观察图1，猜想∠MBN的度数是多少，并证明你的结论；
（2）将图1中的三角形纸片BMN剪下，如图2，折叠该纸片，猜测MN与BM的数量关系，无需证明．
 

24．（12分）在一次男子马拉松长跑比赛中，随机抽得12名选手所用的时间(单位：分钟)得到如下样本数据：140　146　143　175　125　164　134　155　152　168　162　148

(1)计算该样本数据的中位数和平均数；

(2)如果一名选手的成绩是147分钟，请你依据样本数据的中位数，推断他的成绩如何？

参考答案

一、选择题(每小题3分,共30分)

1、D

2、B

3、C

4、A

5、B

6、B

7、A

8、A

9、A

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、甲

12、-1

13、

14、

15、1

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）16−6；（2）4；.

18、（1）OA 在旋转过程中所扫过的面积为 0.5π ；（1）旋转过程中，当 MN 和 AC 平行时，正方形 OABC 旋转的度数为 25°-11.5°=11.5 度;（3）MN 边上的高为 1（2）在旋转正方形 OABC 的过程中，p 值无变化．见解析.

19、 甲种商品的每件进价为40元，乙种商品的每件进价为48元；甲种商品按原销售单价至少销售20件．

20、 (1)x+1； (2)m-3，-4.

21、 (1)；(2).

22、

23、（1）30º，见解析．（2）

24、 (1)中位数为150分钟，平均数为151分钟．

(2)见解析