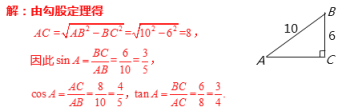
湘教版九年级上册4.2 正切优质课课件ppt

回顾知识

+

导入新课

在上节课中，我们已经学习了有关正弦、余弦的定义，以及特殊角度的正弦、余弦的值。而我们这节课要进一步探究直角三角形两直角边的关系。在上新课之前，我们一起回忆下前面学习的知识。

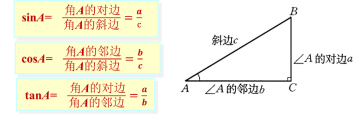
sinα=

cosα=

sin30°= sin45°=  sin60°=

cos60°= sin45°=  cos30°=

锐角三角函数：

1、sinA、cosA是在直角三角形中定义的，∠A是锐角.

   (注意数形结合，构造直角三角形）.

2、sinA、 cosA是一个比值（数值）.。

3、sinA、 cosA的大小只与∠A的大小有关，而与直角三角形的边长无关.

面我们已经研究了直角三角形中的对边与斜边、邻边与斜边的关系。

知道：在直角三角形中， 当一个锐角的大小确定时， 那么不管这个三角形的大小如何， 这个锐角的直角边与斜边的比值也就确定（是一个常数）. 那么这个锐角的对边与邻边的比值是否也是一个常数呢？

为一个常数？

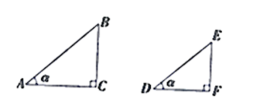
如图，△ABC和△A’B’C’都是直角三角形，其中，∠A=∠D=∠α，∠C=∠F=90°，则吗？为什么？

∵∠A=∠D=∠α，∠C=∠F=90°，

∴Rt△ABC∽Rt△DEF

∴，即 BC·DF=AC·EF

∴

在直角三角形中，当锐角α的度数一定时，不管三角形的大小如何，∠ α的对边与邻边的比是一个固定值.

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

+

例题讲解

讲授新课

+

例题讲解

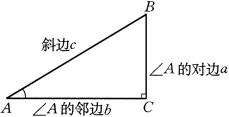
从刚刚导入新课的探究中，我们可以得正切的定义：

      在直角三角形中，我们把锐角A的对边与邻边的比叫做∠A的正切，记作tan A.

tanA=

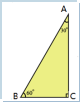
【探究知识】 1.如何求tan30°、tan60°的值？

解：在直角三角形ABC中，∠C=90°，∠B=60°,∠A=30°.

于是∠A的对边BC=AB.

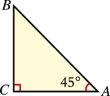
∴AC2=AB2-BC2=（2BC）2-BC2=3BC2.

∴AC=

因此tan30°== ；　 tan60°==

2.如何求 sin 45°的值？

解：在Rt△ABC中，∠C=90°，∠A=45°.

于是 ∠B = 45°.

从而AC = BC.

因此tan 45°=

接下来，我们看一些具体的例子：

【例1】计算：tan45°+tan²30°·tan²60°

解：原式=1+（）²·

     =1+1

     =2

从正弦、余弦、正切的定义看到，任意给定一个锐角A,都有唯一确定的比值sin A(或cos A, tan A)与它对应.并且我们还知道，当锐角a变化时，它的比值sin A(cos A, tan A)也随之变化.因此，我们把锐角A的正弦、余弦和正切统称为角A的锐角三角函数.

 对于锐角三角函数，它们之间有什么关系呢？

tanA

结论：tanA

【例2】计算：2tan45°sin30°+3tan²30°+tan²60°·cos30°

解：原式=2×1×+3×（）²+×

     =1+3×+3×

     =1+1+×

      =2+

我们对这部分的内容进行一个小结：

【例3】如图，在 Rt△ABC 中，∠C=90°，AB=10，BC=6，求sinA，cosA，tanA的值.

对于一般锐角α（30°，45°，60°除外）的正切值， 我们可以利用计算器来求.

1.已知角的度数，求正切值：

例：求25°角的余弦值:在计算器上依次按键，                     的显示结果为0.6427….

2.如果已知正切值，我们也可以利用计算器求出它的对应锐角.

例，已知tanα = 0.391，依次按键，，显示结果为40.000…，表示角α 约等于40°.

【做一做】利用计算器计算：

（1） tan 21°15 ′ ≈      0.3888    （精确到0.0001）；

（2） tan 89° 27 ′≈  104.1709   （精确到0.0001）；

（3） 若tan α = 1.2862， 则α ≈  52.1   (精确到0.1°）；

（4） 若tan α = 108.5729， 则α ≈  89.5 （精确到0.1°）.

结合导入的思考和老师的讲解，利用探究理解和掌握正切的概念、特殊角的正余弦值以及正切值,并能进行简单的计算。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

讲授知识，让学生掌掌握正切的概念、特殊角的正余弦值以及正切值,并能进行简单的计算

让学生知道本节课的学习内容和重点。

让学生知道本节课的学习内容和重点。

课堂练习

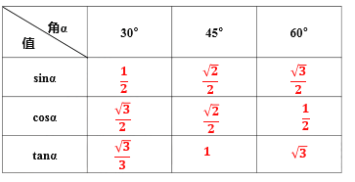
1．填空：

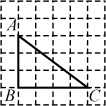
2．在Rt△ABC中，∠A＝90°，AC＝5，AB＝12，那么tan B的值是(     A  )

1.     B.  C.   D. 

3．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tan A等于(   D)

A.     B.  C.    D.

4．用计算器求下列锐角的正切值；(精确到0.000 1)

(1)32°；　 　(2)43°5′；　 　(3)65°23′.

0.6249        0.9352        2.1825

5．已知下列正切值，用计算器求对应的锐角α.(精确0.1°)

(1)tan α＝1.482 6；　　(2)tan α＝7.915 9；

56.0°          82.8°

6．求下列各式的值：

(1)sin 60°tan 30°－2cos230°tan 45°；

(2)＋.

解：（1）原式=1.

（2）原式=

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：

跟着老师回忆知识，并记忆本节课的知识。

帮助学生加强记忆知识。

板书

正切

借助板书，让学生知识本节课的重点。

作业

教材第119页练习第1、2、3、4题.