


2023年高考数学真题模拟试题专项汇编:(8)不等式、推理与证明、算法初步(含答案)
展开
这是一份2023年高考数学真题模拟试题专项汇编:(8)不等式、推理与证明、算法初步(含答案),共6页。
(8)不等式、推理与证明、算法初步——2023年高考数学真题模拟试题专项汇编1. 【2023年全国甲卷理科】若x,y满足约束条件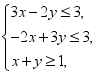 则
则![]() 的最大值为__________.2. 【2023年全国乙卷理科】若x,y满足约束条件
的最大值为__________.2. 【2023年全国乙卷理科】若x,y满足约束条件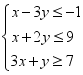 ,则
,则![]() 的最大值为__________.3. 【2023年全国乙卷文科】已知实数x,y满足
的最大值为__________.3. 【2023年全国乙卷文科】已知实数x,y满足![]() ,则
,则![]() 的最大值是( )A.
的最大值是( )A.![]() B.4 C.
B.4 C.![]() D.724. 【2023年天津卷】不等式
D.724. 【2023年天津卷】不等式的解集为__________.5. 【2023年全国甲卷理科】执行下边的程序框图,则输出的
![]() ( )
( )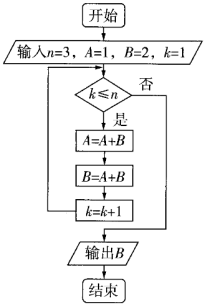 A.21 B.34 C.55 D.896. 【2023年上海卷】【多选】在平面上,若曲线
A.21 B.34 C.55 D.896. 【2023年上海卷】【多选】在平面上,若曲线![]() 具有如下性质:存在点M,使得对于任意的点
具有如下性质:存在点M,使得对于任意的点![]() ,都有
,都有![]() 使得
使得![]() ,则称这条曲线为“自相关曲线”.下列两个命题的真假情况为( )①所有椭圆都是“自相关曲线”.②存在是“自相关曲线”的双曲线.A.①假命题,②真命题 B.①真命题,②假命题C.①真命题,②真命题 D.①假命题,②假命题7. 【2023年四川内江模拟】“
,则称这条曲线为“自相关曲线”.下列两个命题的真假情况为( )①所有椭圆都是“自相关曲线”.②存在是“自相关曲线”的双曲线.A.①假命题,②真命题 B.①真命题,②假命题C.①真命题,②真命题 D.①假命题,②假命题7. 【2023年四川内江模拟】“![]() ,
,![]() ”是“
”是“![]() ”的条件.A.充分不必要 B.必要不充分C.充要 D.既不充分也不必要8. 【2023年福建省模拟】已知
”的条件.A.充分不必要 B.必要不充分C.充要 D.既不充分也不必要8. 【2023年福建省模拟】已知![]() ,则下列结论正确的是( )A.
,则下列结论正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 的最小值为69. 【2023年湖北天门模拟】【多选】已知
的最小值为69. 【2023年湖北天门模拟】【多选】已知![]() ,
,![]() 且
且![]() ,则下列结论中正确的是( )A.
,则下列结论中正确的是( )A.![]() 有最小值
有最小值![]() B.
B.![]() 可以取到0C.
可以取到0C.![]() 有最大值
有最大值![]() D.
D.![]() 有最小值210. 【2023年浙江省模拟】已知a,
有最小值210. 【2023年浙江省模拟】已知a,![]() ,则
,则![]() 的最大值为____________.
的最大值为____________.
答案以及解析1.答案:15解析:根据不等式组作出可行域如图所示,作出直线![]() 并平移,由图可知,当平移后的直线经过点A时,z取得最大值.根据
并平移,由图可知,当平移后的直线经过点A时,z取得最大值.根据![]() 得
得![]() 所以
所以.
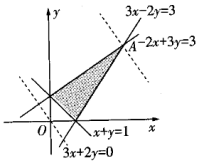 2.答案:8解析:如图,作出可行域,为一封闭三角形区域(包含边界),求出三条边界的交点,分别为
2.答案:8解析:如图,作出可行域,为一封闭三角形区域(包含边界),求出三条边界的交点,分别为![]() ,
,,
![]() .作出直线
.作出直线并平移,当直线
![]() 过点B时截距
过点B时截距取得最小值,即z取得最大值,所以
![]() .
. 3.答案:C解析:将方程
3.答案:C解析:将方程化为
![]() ,其表示圆心为
,其表示圆心为,半径为3的圆.设
![]() ,数形结合知,只有当直线
,数形结合知,只有当直线与圆相切时,z才能取到最大值,此时
![]() ,解得
,解得,故
![]() 的最大值为
的最大值为![]() ,故选C.4.答案:
,故选C.4.答案:![]() 解析:由
解析:由![]() 得
得![]() ,即
,即![]() ,故不等式
,故不等式![]() 的解集是
的解集是![]() .5.答案:B解析:按程序框图执行程序如下:
.5.答案:B解析:按程序框图执行程序如下:![]() 成立,则
成立,则![]() ,
,![]() ,
,![]() ;
;![]() 成立,则
成立,则![]() ,
,![]() ,
,![]() ;
;![]() 成立,则
成立,则![]() ,
,![]() ,
,![]() ;
;![]() 不成立,则输出
不成立,则输出![]() ,故选B.6.答案:B解析:对于命题①,设椭圆
,故选B.6.答案:B解析:对于命题①,设椭圆![]() 的长轴为AB,在AB的延长线上能找到一点M,使
的长轴为AB,在AB的延长线上能找到一点M,使![]() .不妨设
.不妨设![]() ,则
,则![]() ,
,![]() ,即
,即![]() ,易知
,易知![]() 也在此范围内,不妨让
也在此范围内,不妨让![]() 取最大值,
取最大值,![]() 取最小值,假设
取最小值,假设![]() 成立,则
成立,则![]() ,得
,得![]() ,故存在
,故存在![]() 使假设成立,当
使假设成立,当![]() 时,若
时,若![]() 由
由![]() 逐渐减小为
逐渐减小为![]() ,则一定有
,则一定有![]() ,使得
,使得![]() ,故存在点M,使得对于任意的点
,故存在点M,使得对于任意的点![]() ,都有
,都有![]() 使得
使得![]() ,
,![]() 椭圆C是“自相关曲线”.由椭圆的性质知所有椭圆都是“自相关曲线”,故①为真命题.对于命题②,由题意,点P的位置不固定且双曲线不封闭,
椭圆C是“自相关曲线”.由椭圆的性质知所有椭圆都是“自相关曲线”,故①为真命题.对于命题②,由题意,点P的位置不固定且双曲线不封闭,![]() 可取无穷大.如果M在双曲线上,则会存在P和M重合的情况,不符合题意,故M不在双曲线上.假设存在点M,使得对于任意的
可取无穷大.如果M在双曲线上,则会存在P和M重合的情况,不符合题意,故M不在双曲线上.假设存在点M,使得对于任意的![]() ,都有
,都有![]() 使得
使得![]() ,若
,若![]() 取无穷大,则
取无穷大,则![]() ,
,![]() ,
,![]() ,
,![]() 不会趋近于0,故假设不成立,
不会趋近于0,故假设不成立,![]() 不存在是“自相关曲线”的双曲线,故②为假命题.故选B.7.答案:A解析:当
不存在是“自相关曲线”的双曲线,故②为假命题.故选B.7.答案:A解析:当![]() ,
,![]() 时,
时,![]() 成立,当
成立,当![]() 时,取
时,取![]() ,
,![]() 满足
满足![]() ,但是不满足
,但是不满足![]() ,
,![]() ,所以“
,所以“![]() ,
,![]() ”是“
”是“![]() ”的充分不必要条件.故选:A.8.答案:AC解析:A:
”的充分不必要条件.故选:A.8.答案:AC解析:A:![]() ,故A正确;B:
,故A正确;B:![]() ,
,![]() ,显然满足条件,故B错误;C:
,显然满足条件,故B错误;C:![]() ,故C正确;D:
,故C正确;D:![]() ,由于
,由于![]() 在
在![]() 上为增函数,故最小值为5,D错误.故选AC.9.答案:AD解析:因为
上为增函数,故最小值为5,D错误.故选AC.9.答案:AD解析:因为![]() ,当且仅当
,当且仅当![]() ,即
,即![]() ,
,![]() 时等号成立,故A正确;因为
时等号成立,故A正确;因为![]() 时,
时,![]() ,而
,而![]() ,得出
,得出![]() ,
,![]() ,
,![]() 时等号成立,故
时等号成立,故![]() 不成立,故B错误;因为
不成立,故B错误;因为![]() ,当且仅当
,当且仅当![]() ,即
,即![]() ,
,![]() 时等号成立,而
时等号成立,而![]() ,故等号不成立,故C错误;由
,故等号不成立,故C错误;由![]() 知,
知,![]() ,当且仅当
,当且仅当![]() 时,即
时,即![]() ,
,![]() 时等号成立,故D正确.故选:AD10. 答案:4解析:当
时等号成立,故D正确.故选:AD10. 答案:4解析:当![]() 时,
时,![]() ,又a,
,又a,![]() ,显然当
,显然当![]() 或2,
或2,![]() 时,该式取得最大值
时,该式取得最大值![]() .当
.当![]() 时,
时,![]() ,又a,
,又a,![]() ,显然当
,显然当![]() ,
,![]() 时,该式取得最大值
时,该式取得最大值![]() .综上所述,
.综上所述,![]() 的最大值为4.故答案为:4.
的最大值为4.故答案为:4.
相关试卷
这是一份高中数学高考专题11 不等式、推理与证明、算法初步、复数——2020年高考真题和模拟题理科数学分项汇编(学生版),共11页。试卷主要包含了【2020年新高考全国Ⅰ】等内容,欢迎下载使用。
这是一份高中数学高考专题11 不等式、推理与证明、算法初步、复数——2020年高考真题和模拟题理科数学分项汇编(教师版含解析),共28页。试卷主要包含了【2020年新高考全国Ⅰ】等内容,欢迎下载使用。
这是一份高中数学高考专题10 不等式、推理与证明、算法初步、复数-2021年高考真题和模拟题数学(文)分项汇编(全国通用)(解析版),共24页。试卷主要包含了已知,,,则等内容,欢迎下载使用。










