高考数学一轮复习夯基练习：圆锥曲线的综合问题(含答案)

这是一份高考数学一轮复习夯基练习：圆锥曲线的综合问题(含答案)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
夯基练习 圆锥曲线的综合问题一 、选择题1.过双曲线C：－=1的左焦点作倾斜角为的直线l，则直线l与双曲线C的交点情况是(　　)A．没有交点                      B．只有一个交点C．有两个交点且都在左支上        D．有两个交点分别在左、右两支上  2.已知直线l与抛物线C：y2=4x相交于A，B两点，若线段AB的中点为(2,1)，则直线l的方程为(　　)A．y=x－1          B．y=－2x＋5     C．y=－x＋3         D．y=2x－3  3.过抛物线y2=4x的焦点F的直线l与抛物线交于A，B两点，若A，B两点的横坐标之和为，则|AB|=(　　)A.          B.          C．5          D.  4.过抛物线y2=4x的焦点作直线交抛物线于A，B两点，若O为坐标原点，则∙=(   )A.﹣1                         B.﹣2                          C.﹣3                             D.﹣45.已知双曲线C：－=1(a＞0，b＞0)，过点P(3,6)的直线l与C相交于A，B两点，且AB的中点为N(12,15)，则双曲线C的离心率为(　　)A．2              B.           C.             D.   6.已知抛物线E：y2=2px(p＞0)的焦点为F，过F且斜率为1的直线交E于A，B两点，线段AB的中点为M，线段AB的垂直平分线交x轴于点C，MN⊥y轴于点N，若四边形CMNF的面积等于7，则E的方程为(　　)A．y2=x              B．y2=2x          C．y2=4x            D．y2=8x  7.已知双曲线(a＞0，b＞0)的左、右焦点分别为F1，F2，P为双曲线右支上一点(异于右顶点)，△PF1F2的内切圆与x轴切于点(2，0).过F2作直线l与双曲线交于A，B两点，若使=b2的直线l恰有三条，则双曲线离心率的取值范围是(　　  )A.(1，)       B.(1，2)             C.(，＋∞)         D.(2，＋∞) 8.双曲线C：(a＞0，b＞0)焦点分别为F1，F2，在双曲线C右支上存在点P，使得△PF1F2的内切圆半径为a，圆心记为M，△PF1F2的重心为G，满足MG∥F1F2，则双曲线C离心率为(  )                                          A.                      B.                         C.2                            D.9.已知点A是抛物线C：x2=2py(p＞0)的对称轴与准线的交点，过点A作抛物线C的两条切线，切点分别为P，Q，若△APQ的面积为4，则p的值为(　　)A.0.5             B．1          C.1.5             D．2  10.已知F1(－c，0)，F2(c，0)为椭圆(a＞b＞0)的两个焦点，P为椭圆上一点且·=c2，则此椭圆离心率的取值范围是(　  　)11.已知双曲线x2－y2=1的左、右顶点分别为A1，A2，动直线l：y=kx＋m与圆x2＋y2=1相切，且与双曲线左、右两支的交点分别为P1(x1，y1)，P2(x2，y2)，则x2－x1的最小值为(　　)A．2            B．2           C．4               D．3  12.双曲线C：(a＞0，b＞0)的左、右焦点分别为F1(－c，0)，F2(c，0)，M，N两点在双曲线C上，且MN∥F1F2，|F1F2|=4|MN|，线段F1N交双曲线C于点Q，且|F1Q|=|QN|，则双曲线C的离心率为(　　)A.2              B.                C.                 D. 二 、填空题13.抛物线C：y2=2px(p＞0)，直线l：y=(x－1)，l与C交A，B两点，若|AB|=，则p=____.  14.设抛物线x2=4y的焦点为F，点A，B在抛物线上，且满足=λ，若||=，则λ的值为________．  15.以下关于圆锥曲线的4个命题中：(1)方程2x2﹣5x+2=0的两实根可分别作为椭圆和双曲线的离心率；(2)设A,B为平面内两个定点,若|PA|﹣|PB|=k(k＞0),则动点P的轨迹为双曲线；(3)若方程kx2+(4﹣k)y2=1表示椭圆,则k的取值范围是(0,4)；(4)双曲线﹣=1与椭圆+y2=1有相同的焦点.其中真命题的序号为　   　(写出所有真命题的序号).16.已知直线MN过椭圆＋y2=1的左焦点F，与椭圆交于M，N两点．直线PQ过原点O且与直线MN平行，直线PQ与椭圆交于P，Q两点，则=________.   三 、解答题17.已知F为抛物线E：y2=4x的焦点，过点P(0,2)作两条互相垂直的直线m，n，直线m交E于不同的A，B两点，直线n交E于不同的两点C，D，记直线m的斜率为k.(1)求k的取值范围；(2)设线段AB，CD的中点分别为点M，N，证明：直线MN过定点Q(2,0)．                     18.已知椭圆＋=1(a>b>0)的左，右焦点分别为F1，F2，且|F1F2|=6，直线y=kx与椭圆交于A，B两点．(1)若△AF1F2的周长为16，求椭圆的标准方程；(2)若k=，且A，B，F1，F2四点共圆，求椭圆离心率e的值；(3)在(2)的条件下，设P(x0，y0)为椭圆上一点，且直线PA的斜率k1∈(－2，－1)，试求直线PB的斜率k2的取值范围．                         19.设O为坐标原点，动点M在椭圆C上，过M作x轴的垂线，垂足为N，点P满足.（1）求点P的轨迹方程；（2）设点 在直线x=-3上，且.证明过点P且垂直于OQ的直线l过C的左焦点F.          20.如图，设抛物线的焦点为F，抛物线上的点A到y轴的距离等于|AF|-1.（1）求p的值；（2）若直线AF交抛物线于另一点B，过B与x轴平行的直线和过F与AB垂直的直线交于点N，AN与x轴交于点M.求M的横坐标的取值范围.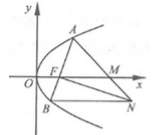                
参考答案1.答案为：D；解析：直线l的方程为y=，代入C：－=1，整理得23x2－8x－160=0，Δ=(－8)2＋4×23×160＞0，所以直线l与双曲线C有两个交点，由一元二次方程根与系数的关系得两个交点横坐标符号不同，故两个交点分别在左、右两支上．  2.答案为：D；解析：设A(x1，y1)，B(x2，y2)，则有①－②得y－y=4(x1－x2)，由题可知x1≠x2.∴===2，即kAB=2，∴直线l的方程为y－1=2(x－2)，即2x－y－3=0.故选D.  3.答案为：D；解析：过抛物线的焦点的弦长公式为|AB|=p＋x1＋x2.∵p=2，∴|AB|=2＋=.4.C.5.答案为：B；解析：设A(x1，y1)，B(x2，y2)，由AB的中点为N(12，15)，得x1＋x2=24，y1＋y2=30，由两式相减得：=，则==.由直线AB的斜率k==1，∴=1，则=，∴双曲线的离心率e===.  6.解析：F，直线AB的方程为y=x－.联立得方程组可得x2－3px＋=0，设A(x1，y1)，B(x2，y2)，则x1＋x2=3p，则y1＋y2=x1＋x2－p=2p，∴M，∴N(0，p)，直线MC的方程为y=－x＋.∴C，∴四边形CMNF的面积为S梯形OCMN－S△ONF=－··p==7，又p＞0，∴p=2，即抛物线E的方程为y2=4x.故选C.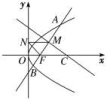  7.答案为：C； 8.C.              9.答案为：D；解析：设过点A与抛物线相切的直线方程为y=kx－.由得x2－2pkx＋p2=0，由Δ=4k2p2－4p2=0，可得k=±1，则Q，P，∴△APQ的面积为×2p×p=4，∴p=2.故选D.  10.答案为：C； 11.答案为：A；解析：∵l与圆相切，∴原点到直线的距离d==1，∴m2=1＋k2，由得(1－k2)x2－2mkx－(m2＋1)=0，∴∴k2＜1，∴－1＜k＜1，由于x1＋x2=，∴x2－x1===，∵0≤k2＜1，∴当k2=0时，x2－x1取最小值2.故选A.  12.答案为：D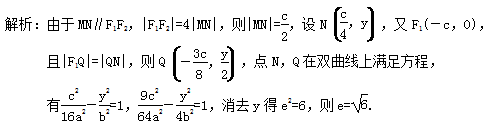；  二 、填空题13.答案为：2；解析：由消去y，得3x2－(2p＋6)x＋3=0，设A(x1，y1)，B(x2，y2)，由根与系数的关系，得x1＋x2=，x1x2=1，所以|AB|=2=2 =，所以p=2.  14.答案为：0.5；解析：设A(x1，y1)，B(x2，y2)，由抛物线x2=4y得焦点F的坐标为(0,1)，准线方程为y=－1，∵||=，∴y1＋1=，解得y1=，∴x1=±，由抛物线的对称性取x1=，∴A，∴直线AF的方程为y=－x＋1，由解得或∴B(－2，2)，∴||=2＋1=3，∵=λ，∴||=λ||，∴=3λ，解得λ=.  15.答案为：(1),(4)；16.答案为：2；解析：由题意知，直线MN的斜率不为0，设直线MN的方程为x=my＋1，则直线PQ的方程为x=my.设M(x1，y1)，N(x2，y2)，P(x3，y3)，Q(x4，y4).⇒(m2＋2)y2＋2my－1=0⇒y1＋y2=－，y1y2=－.∴|MN|=|y1－y2|=2·.⇒(m2＋2)y2－2=0⇒y3＋y4=0，y3y4=－.∴|PQ|=|y3－y4|=2 .故=2.   三 、解答题17.解：(1)由题设可知k≠0，所以直线m的方程为y=kx＋2，与y2=4x联立，整理得ky2－4y＋8=0.①由Δ1=16－32k＞0，解得k＜.直线n的方程为y=－x＋2，与y2=4x联立，整理得y2＋4ky－8k=0，由Δ2=16k2＋32k＞0，解得k＞0或k＜－2.所以故k的取值范围为(－∞，－2)∪.(2)证明：设A(x1，y1)，B(x2，y2)，M(x0，y0)．由①得，y1＋y2=，则y0=，x0=－，则M.同理可得N(2k2＋2k，－2k)．直线MQ的斜率kMQ==－，直线NQ的斜率kNQ==－=kMQ，所以直线MN过定点Q(2,0)．   18.解：(1)由题意得c=3，根据2a＋2c=16，得a=5.结合a2=b2＋c2，解得a2=25，b2=16.所以椭圆的方程为＋=1.(2)由得x2－a2b2=0.设A(x1，y1)，B(x2，y2)．所以x1＋x2=0，x1x2=，由AB，F1F2互相平分且共圆，易知，AF2⊥BF2，因为=(x1－3，y1)，=(x2－3，y2)，所以·=(x1－3)(x2－3)＋y1y2=x1x2＋9=0.即x1x2=－8，所以有=－8，结合b2＋9=a2，解得a2=12，所以离心率e=.(3)由(2)的结论知，椭圆方程为＋=1，由题可知A(x1，y1)，B(－x1，－y1)，k1=，k2=，所以k1k2=，又==－，即k2=－，由－2<k1<－1可知，<k2<.即直线PB的斜率k2∈.  19.解：20.解：