

高考数学一轮复习作业本1.5 函数的奇偶性与周期性(含答案)
展开2020高考数学(理数)复习作业本1.5 函数的奇偶性与周期性
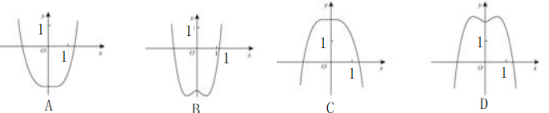
2.已知函数y=f(x)是偶函数,其图像与x轴有四个交点,则方程f(x)=0的所有实数根的和为( )
A.4 B.2 C.1 D.0
3.函数y=f(x)是奇函数,图象上有一点为(a,f(a)),则图象必过点( )
A.(a,f(-a)) B.(-a,f(a)) C.(-a,-f(a)) D.![]()
4.设f(x)是定义在R上的偶函数,且在(0,+∞)上是减函数,若a<0且a+b>0,则( )
A.f(a)>f(b) B.f(a)=f(b)
C.f(a)<f(b) D.f(a)与f(b)的大小不确定
A.f(x)-f(-x)≥0 B.f(x)-f(-x)≤0 C.f(x)·f(-x)≤0 D.f(x)·f(-x)>0
6.对任意的实数x都有f(x+2)-f(x)=2f(1),若y=f(x-1)的图象关于x=1对称,且f(0)=2,则f(2 019)+f(2 020)=( )
A.0 B.2 C.3 D.4
7.若函数f(x)为奇函数,且在(0,+∞)上是增函数,又f(2)=0,则![]() 解集为( )
解集为( )
A.(-2,0)∪(0,2) B.(-∞,-2)∪(0,2)
C.(-∞,-2)∪(2,+∞) D.(-2,0)∪(2,+∞)
8.设f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则x·f(x)<0的解集是( )
A.{x∣-3<x<0或x>3} B.{x∣<x<-3或0<x<3}
C.{x∣<x<-3或x>3} D.{x∣-3<x<0或0<x<3}
9.已知函数f(x)为偶函数,且其图象与x轴有四个交点,则方程f(x)=0的所有实根之和为________.
10.已知定义在R上的奇函数f(x),当x>0时,f(x)=x2+|x|-1,那么x<0时,f(x)= .
11.若y=(m-1)x2+2mx+3是偶函数,则m=_________![]() .
.
12.已知f(x)是偶函数,g(x)是奇函数,若![]() ,则f(x)的解析式为_______.
,则f(x)的解析式为_______.
13.已知二次函数f(x)=x2-(a-1)x+5在区间(0.5,1)上是增函数,求:(1)实数a的取值范围;(2)f(2)的取值范围.
14.定义在(-1,1)上的奇函数f(x)是减函数,且f(1-a)+f(1-a2)<0,求实数a的取值范围.
15.已知y=f(x)是定义在(-∞,+∞)上的奇函数,且在[0,+∞)上为增函数,
(1)求证:函数在(-∞,0)上也是增函数;
(2)如果f(0.5)=1,解不等式-1<f(2x+1)≤0.
(1)证明:函数f(x)在(1,+∞)上单调递减;
(2)记函数g(x)=f(x+1)-1,判断函数g(x)的奇偶性,并加以证明.
解析:∵ a<0且a+b>0,∴b>-a>0,又函数 f(x)在(0,+∞)上是减函数,
∴ f(b)<f(-a),又f(x)是定义在R上的偶函数,∴f(b)<f(a).
解析:选B.
∵y=f(x-1)的图象关于x=1对称,则函数y=f(x)的图象关于x=0对称,即函数f(x)是偶函数.
令x=-1,则f(-1+2)-f(-1)=2f(1),即f(1)-f(1)=2f(1)=0,即f(1)=0.
则f(x+2)-f(x)=2f(1)=0,即f(x+2)=f(x),
即函数的周期是2,又f(0)=2,则f(2 019)+f(2 020)=f(1)+f(0)=0+2=2,故选B.
7.A 解析:因为函数f(x)为奇函数,且在(0,+∞)上是增函数,f(2)=0,所以x>2或-2<x<0时,f(x)>0;x<-2或0<x<2时,f(x)<0.<0,即<0,可知-2<x<0或0<x<2.
11.答案为:0;解析:因为函数y=(m-1)x2+2mx+3为偶函数,∴f(-x)=f(x),
即(m-1)(-x)2+2m(-x)+3=(m—1)x2+2mx+3,整理,得m=0.
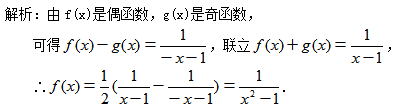
13.解:(1)∵对称轴![]() 是决定f(x)单调性的关键,联系图象可知,
是决定f(x)单调性的关键,联系图象可知,
只需![]() ;
;
(2)∵f(2)=22-2(a-1)+5=-2a+11又∵a≤2,∴-2a≥-4 ∴f(2)=-2a+11≥-4+11=7![]() .
.
14. [解析] 由f(1-a)+f(1-a2)<0及f(x)为奇函数得,f(1-a)<f(a2-1),
∵f(x)在(-1,1)上单调减,∴
15. (1)证明:设x1、x2是(-∞,0]上任意两个不相等的实数,且x1<x2,
则-x1,-x2∈[0,+∞),且-x1>-x2,Δx=x2-x1>0,Δy=f(x2)-f(x1).
∵f(x)是奇函数,且在[0,+∞)上是增函数,-x1>-x2,∴f(-x1)>f(-x2).
又∵f(x)为奇函数,∴f(-x1)=-f(x1),f(-x2)=-f(x2).
∴-f(x1)>-f(x2),即f(x1)<f(x2),即Δy=f(x2)-f(x1)>0.
∴函数f(x)在(-∞,0]上也是增函数.
(2)解:∵f(x)是R上的奇函数,∴f(0)=0,f(-0.5)=-f(0.5)=-1.
由-1<f(2x+1)≤0,得f(-0.5)<f(2x+1)≤f(0).
又∵f(x)在(-∞,0)上是增函数,∴-0.5<2x+1≤0,得-0.75<x≤-0.5.
∴不等式的解集为{x|-0.75<x≤-0.5}.
![]() ,
,
∴![]() ,∴
,∴![]() 在
在![]() 上递减.
上递减.
(2)![]() ,
,![]() 是奇函数,
是奇函数,
证明如下:∵![]() 的定义域为
的定义域为![]() 关于原点对称,
关于原点对称,
![]() ,∴
,∴![]() 是奇函数.
是奇函数.
人教版高考数学一轮复习考点规范练7函数的奇偶性与周期性含答案: 这是一份人教版高考数学一轮复习考点规范练7函数的奇偶性与周期性含答案,共4页。试卷主要包含了故选B等内容,欢迎下载使用。
高考数学一轮复习课时质量评价8函数的奇偶性与周期性含答案: 这是一份高考数学一轮复习课时质量评价8函数的奇偶性与周期性含答案,共6页。
高考数学一轮复习 专题3.3 函数的奇偶性与周期性(练): 这是一份高考数学一轮复习 专题3.3 函数的奇偶性与周期性(练),文件包含专题33函数的奇偶性与周期性练教师版docx、专题33函数的奇偶性与周期性练学生版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。













