专题01 集合与常用逻辑用语(公式、定理、结论图表)-备战2024年新高考数学必背知识手册
展开集合与常用逻辑用语(公式、定理、结论图表)


1.集合的有关概念
(1)集合元素的三大特性:确定性、无序性、互异性.
(2)元素与集合的两种关系:属于,记为![]() ;不属于,记为
;不属于,记为![]() .
.
(3)集合的三种表示方法:列举法、描述法、图示法.
(4)五个特定的集合
集合 | 自然数集 | 正整数集 | 整数集 | 有理数集 | 实数集 |
符号 | N*或N+ |
2.集合间的基本关系
| 文字语言 | 符号语言 | |
集合间的 基本关系 | 相等 | 集合A与集合B中的所有元素都相同 | A=B |
子集 | 集合A中任意一个元素均为集合B中的元素 | A⊆B | |
真子集 | 集合A中任意一个元素均为集合B中的元素,且集合B中至少有一个元素不是集合A中的元素 |
| |
空集 | 空集是任何集合的子集,是任何非空集合的真子集 | ||
3.集合的基本运算
| 集合的并集 | 集合的交集 | 集合的补集 |
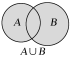
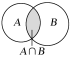
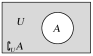
符号表示 | A∪B | A∩B | 若全集为U,则集合A的补集为∁UA |
图形表示 |
|
|
|
集合表示 | {x|x∈A,或x∈B} | {x|x∈A,且x∈B} | {x|x∈U,且x∉A} |
4.集合的运算性质
(1)A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A.
,A∩B=B∩A.
(2)A∪A=A,A∪![]() =A,A∪B=B∪A.
=A,A∪B=B∪A.
(3)A∩(∁UA)=![]() ,A∪(∁UA)=U,∁U(∁UA)=A.
,A∪(∁UA)=U,∁U(∁UA)=A.
5.常用结论
(1)空集性质:①空集只有一个子集,即它的本身,∅⊆∅;
②空集是任何集合的子集(即∅⊆A);
空集是任何非空集合的真子集(若A≠∅,则∅![]() A).
A).
(2)子集个数:若有限集A中有n个元素,
则A的子集有2n个,真子集有2n-1个,非空真子集有![]() 个.
个.
典例1:已知集合![]() ,
,![]() ,则
,则![]() 的子集的个数为( )
的子集的个数为( )
A.3 B.4 C.7 D.8
【答案】B
【详解】因为集合![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() 的子集的个数为
的子集的个数为![]() 个.故选B.
个.故选B.
典例2:已知集合![]() ,则集合
,则集合![]() 的真子集的个数为( )
的真子集的个数为( )
A.32 B.31 C.16 D.15
【答案】D
【详解】由题意得![]() ,
,
其真子集有![]() 个.故选D.
个.故选D.
(3)A∩B=A⇔A⊆B;A∪B=A⇔A⊇B.
(4)(∁UA)∩(∁UB)=∁U(A∪B),(∁UA)∪(∁UB)=∁U(A∩B) .
6.充分条件、必要条件与充要条件的概念
若p ⇒ q,则p是q的充分条件,q是p的必要条件 | |
p是q的充分不必要条件 | p ⇒ q且q ⇏ p |
p是q的必要不充分条件 | p ⇏ q且q ⇒ p |
p是q的充要条件 | p ⇔ q |
p是q的既不充分也不必要条件 | p ⇏ q且q ⇏ p |
7.充分、必要条件与集合的关系
设p,q成立的对象构成的集合分别为A,B.
(1)p是q的充分条件⇔A⊆B,p是q的充分不必要条件⇔A![]() B;
B;
(2)p是q的必要条件⇔B⊆A,p是q的必要不充分条件⇔B![]() A;
A;
(3)p是q的充要条件⇔A=B.
8.全称量词和存在量词
量词名称 | 常见量词 | 符号表示 |
全称量词 | 所有、一切、任意、全部、每一个等 | |
存在量词 | 存在一个、至少有一个、有些、某些等 |
9.全称命题和特称命题
名称 形式 | 全称命题 | 特称命题 |
语言表示 | 对M中任意一个x,有p(x)成立 | M中存在元素x0,使p(x0)成立 |
符号表示 | ∀x∈M,p(x) | ∃x0∈M,p(x0) |
10.全称命题与特称命题的否定
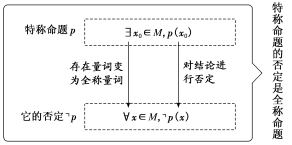
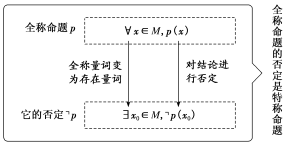
<知识记忆小口诀>
集合平时很常用,数学概念有不同,理解集合并不难,三个要素是关键,元素确定和互译,还有无序要牢记,空集不论空不空,总有子集在其中,集合用图很方便,子交并补很明显.
<解题方法与技巧>
集合基本运算的方法技巧:
(1)当集合是用列举法表示的数集时,可以通过列举集合的元素进行运算,也可借助Venn图运算;
(2)当集合是用不等式表示时,可运用数轴求解.对于端点处的取舍,可以单独检验.
集合常与不等式,基本函数结合,常见逻辑用语常与立体几何,三角函数,数列,线性规划等结合.
充要条件的两种判断方法
(1)定义法:根据p⇒q,q⇒p进行判断.
(2)集合法:根据使p,q成立的对象的集合之间的包含关系进行判断.
充分条件、必要条件的应用,一般表现在参数问题的求解上.解题时需注意:
(1)把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.
(2)要注意区间端点值的检验.尤其是利用两个集合之间的关系求解参数的取值范围时,不等式是否能够取等号决定端点值的取舍,处理不当容易出现漏解或增解的现象.
(3)数学定义都是充要条件.
专题16 计数原理(公式、定理、结论图表)-备战2024年新高考数学必背知识手册: 这是一份专题16 计数原理(公式、定理、结论图表)-备战2024年新高考数学必背知识手册,共11页。试卷主要包含了计数原理,排列,组合,二项式定理,杨辉三角形等内容,欢迎下载使用。
专题15 导数及其应用(公式、定理、结论图表)-备战2024年新高考数学必背知识手册: 这是一份专题15 导数及其应用(公式、定理、结论图表)-备战2024年新高考数学必背知识手册,共8页。试卷主要包含了曲线在点处切线,曲线过点处切线,利用导数求最值,.解决优化问题的步骤,))等内容,欢迎下载使用。
专题14 数列(公式、定理、结论图表)-备战2024年新高考数学必背知识手册: 这是一份专题14 数列(公式、定理、结论图表)-备战2024年新高考数学必背知识手册,共13页。试卷主要包含了定义, 前n项和公式法等内容,欢迎下载使用。