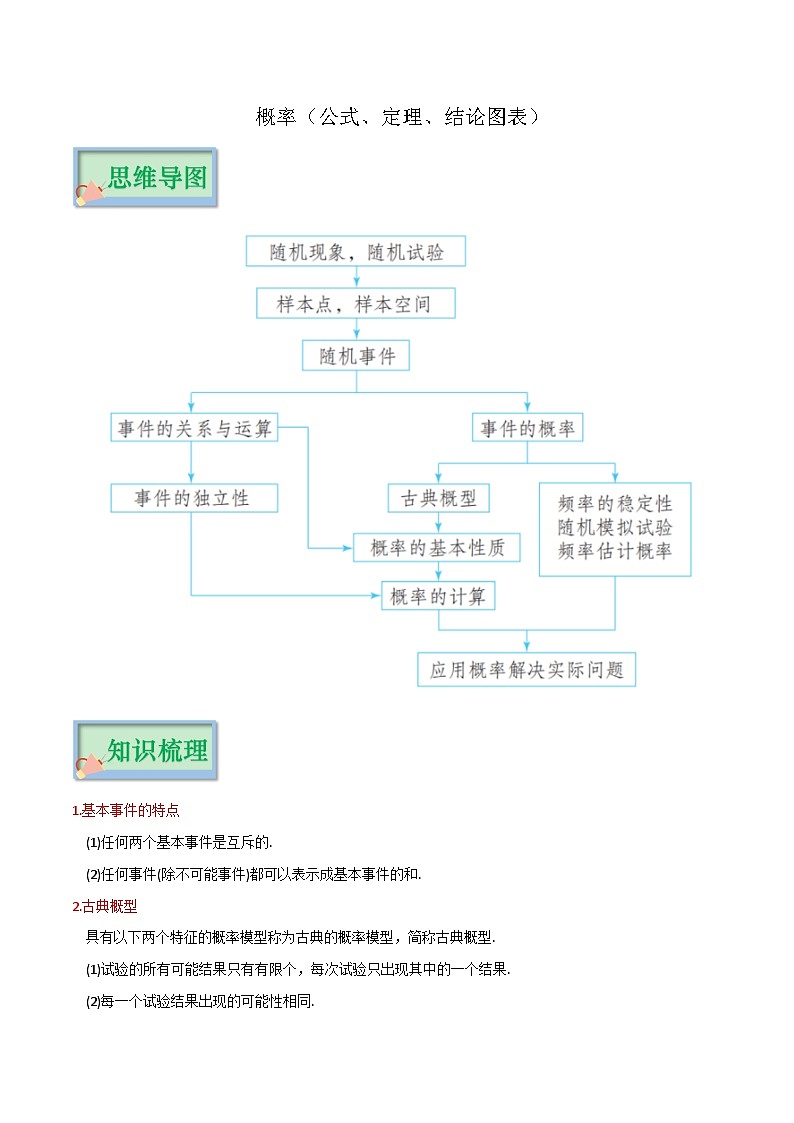
专题10 概率（公式、定理、结论图表）-备战2024年新高考数学必背知识手册

  概率（公式、定理、结论图表）

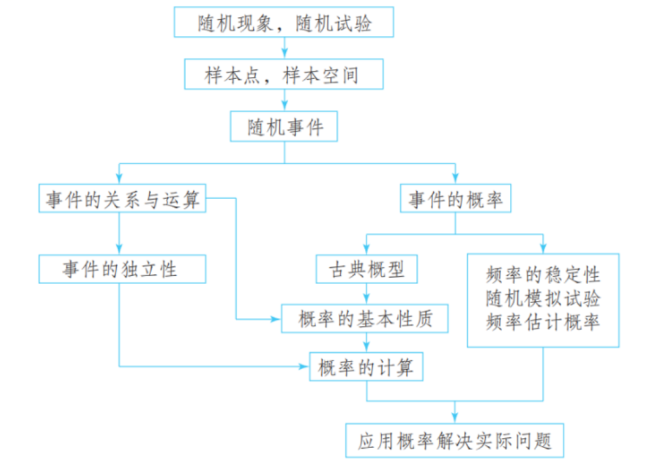
1.基本事件的特点

(1)任何两个基本事件是互斥的.

(2)任何事件(除不可能事件)都可以表示成基本事件的和.

2.古典概型

具有以下两个特征的概率模型称为古典的概率模型，简称古典概型.

(1)试验的所有可能结果只有有限个，每次试验只出现其中的一个结果.

(2)每一个试验结果出现的可能性相同.

【特别提醒】

如果一次试验中可能出现的结果有n个，而且所有结果出现的可能性都相等，那么每一个基本事件的概率都是；如果某个事件A包括的结果有m个，那么事件A的概率P(A)＝.

3. 古典概型的概率公式

P(A)＝.

典例1：5张奖券中有2张是中奖的，首先由甲抽一张，然后由乙抽一张，求：

    (1)甲中奖的概率P(A)；

    (2)甲、乙都中奖的概率P(B)；

    (3)只有乙中奖的概率P(C)；

    (4)乙中奖的概率P(D)．

   【思路点拨】先确定事件总数，再确定四个事件中包含的基本事件个数，用古典概率公式求解．

【解析】甲、乙两人按顺序各抽一张，5张奖券分别为A1，A2，B1，B2，B3，其中A1，A2为中奖券，则基本事件为(A1，A2)，(A1，B1)，(A1，B2)，(A1，B3)，(A2，A1)，(A2，B1)，(A2，B2)，(A2，B3)，(B1，A1)，(B1，A2)，(B1，B2)，(B1，B3)，(B2，A1)，(B2，A2)，(B2，B1)，(B2，B3)，(B3，A1)，(B3，A2)，(B3，B1)，(B3，B2)，共20种．

(1)若“甲中奖”，则有(A1，A2)，(A1，B1)，(A1，B2)，(A1，B3)，(A2，A1)，(A2，B1)，(A2，B2)，(A2，B3)，共8种，故P(A)．

    (2)甲、乙都中奖含有的基本事件有(A1，A2)，(A2，A1)，共2种，所以P(B)＝．

(3)“只有乙中奖”的基本事件有(B1，A1)，(B2，A1)，(B3，A1)，(B1，A2)，(B2，A2)，(B3，A2)，共6种，故．

(4)“乙中奖”的基本事件有(A2，A1)，(B1，A1)，(B2，A1)，(B3，A1)，(Al，A2)，(B1，A2)，(B2，A2)，(B3，A2)，共8种，故．

【总结升华】

1、利用古典概型的计算公式时应注意两点：

(1)所有的基本事件必须是互斥的；

(2)m为事件A所包含的基本事件数，求m值时，要做到不重不漏.

2、古典概型解题步骤：

(1)阅读题目，搜集信息；

(2)判断是否是等可能事件，并用字母表示事件；

(3)求出基本事件总数和事件所包含的结果数；

(4)用公式求出概率并下结论.

4.事件的关系与运算

 5.概率的几个基本性质

(1)概率的取值范围：0≤P(A)≤1.

(2)必然事件的概率P(E)＝1.

(3)不可能事件的概率P(F)＝0.

(4)互斥事件概率的加法公式

①如果事件A与事件B互斥，则P(A∪B)＝P(A)＋P(B).

②若事件B与事件A互为对立事件，则P(A)＝1－P(B).

典例2：经统计，在某储蓄所一个营业窗口等候的人数及相应概率如下：

(1)至多2人排队等候的概率是多少?

(2)至少3人排队等候的概率是多少?

【思路点拨】利用互斥事件概率加法公式计算．

【解析】记“等候的人数为0”为事件A，“1人等候”为事件B，“2人等候”为事件C，“3人等候”为事件D，“4人等候”为事件E，“5人及5人以上等候”为事件F，则易知A、B、C、D、E、F互斥．

    (1)记“至多2人排队等候”为事件G，则G＝A∪B∪C，

∴  P(G)＝P(A+B+C)＝P(A)+P(B)+P(C)

    ＝0.1+0.16+0.3＝0.56．

    (2)记“至少3人排队等候”为事件H，则H＝D∪E∪F，

∴  P(H)＝P(D+E+F)＝P(D)+P(E)+P(F)

＝0.3+0.1+0.04＝0.44．

【总结升华】第(2)问也可以这样解：因为G与H是对立事件，所以P(H)＝1－P(G)＝1－0.56＝0.44．