


江苏省镇江第一中学2023-2024学年高三上学期期初阶段学情检测数学试卷
展开![]() 江苏省镇江第一中学阶段检测试题
江苏省镇江第一中学阶段检测试题
高三数学
考试时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合![]() ,则
,则![]()
A.![]() B.
B.![]()
C.![]() D.2
D.2
2.![]() 的展开式中含
的展开式中含![]() 项的系数是()
项的系数是()
A.-112 B.112 C.-28 D.28
3.某单位为了了解办公楼用电量![]() (度)与气温
(度)与气温![]() 之间的关系,随机统计了四个工作日的用电量与当天平均气温,并制作了对照表:由表中数据得到线性回归方程
之间的关系,随机统计了四个工作日的用电量与当天平均气温,并制作了对照表:由表中数据得到线性回归方程![]() ,当气温为
,当气温为![]() 时,预测用电量为
时,预测用电量为![]()
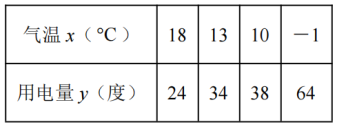
A.68度 B.66度 C.28度 D.12度
4.某一天的课程表要排入语文、数学、英语、物理、化学、生物六门课,如果数学只能排在第一节或者最后一节,物理和化学必须排在相邻的两节,则共有()种不同的排法
A.24 B.144 C.48 D.96
5.已知正方体![]() 的棱长为
的棱长为![]() 是线段
是线段![]() 上的动点且
上的动点且![]() ,则三棱锥
,则三棱锥![]() 的体积为
的体积为![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
6.若随机变量![]() 服从两点分布,其中
服从两点分布,其中![]() 分别为随机变量
分别为随机变量![]() 的均值与方差,则下列结论不正确的是()
的均值与方差,则下列结论不正确的是()
A.![]()
B.![]()
C.![]()
D.![]()
7.设函数![]() 在
在![]() 上满足
上满足![]() ,且当
,且当![]() 时,
时,![]() 成立,若
成立,若![]() ,
,![]() ,的
,的![]() 大大小关系是()
大大小关系是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知随机事件A,![]() 满足
满足![]() ,则下列说法错误的是()
,则下列说法错误的是()
A.不可能事件![]() 与事件A互斥
与事件A互斥
B.必然事件![]() 与事件
与事件![]() 相互独立
相互独立
C.![]()
D.若![]() ,则
,则![]()
二.多选题:本题共4小题,每小题5分,共计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知函数![]() 的导函数
的导函数![]() 的图象如图所示,则下列结论中正确的是()
的图象如图所示,则下列结论中正确的是()
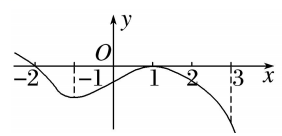
A.![]() 在区间
在区间![]() 上有2个极值点
上有2个极值点
B.![]() 在
在![]() 处取得极小值
处取得极小值
C.![]() 在区间
在区间![]() 上单调递减
上单调递减
D.![]() 在
在![]() 处的切线斜率小于0
处的切线斜率小于0
10.设![]() ,则下列结论正确的是()
,则下列结论正确的是()
A.![]() 的最大值为
的最大值为![]()
B.![]() 的最小值为
的最小值为![]()
C.![]() 的最小值为9
的最小值为9
D.![]() 的最小值为
的最小值为![]()
11.如图,![]() 为圆锥
为圆锥![]() 底面圆
底面圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() 的一点,
的一点,![]() 为
为![]() 的中点,则圆
的中点,则圆![]() 上存在点
上存在点![]() 使()
使()
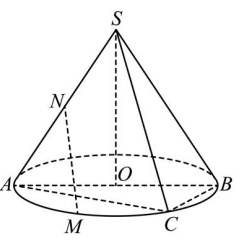
A.![]() C.
C.![]() B.
B.![]() 平面
平面![]() D.
D.![]() 平面
平面![]()
12.随着春节的临近,小王和小张等4位同学准备互相送祝福.他们每人写了一个祝福的贺卡,这四张贺卡收齐后让每人从中随机抽取一张作为收到的新春祝福,则()
A.小王和小张恰好互换了贺卡的概率为![]()
B.已知小王抽到的是小张写的贺卡的条件下,小张抽到小王写的贺卡的概率为![]()
C.恰有一个人抽到自己写的贺卡的概率为![]()
D.每个人抽到的贺卡都不是自己写的概率为![]()
三.填空题:本题共4小题,每小题5分,共计20分.
13.正四棱台的上、下底面边长分别为2,4,侧棱长为![]() ,则其体积为 .
,则其体积为 .
14.某学校组织1200名学生进行“防疫知识测试”.测试后统计分析如下:学生的平均成绩为![]() ,方差为
,方差为![]() .学校要对成绩不低于90分的学生进行表彰.假设学生的测试成绩
.学校要对成绩不低于90分的学生进行表彰.假设学生的测试成绩![]() 近似服从正态分布
近似服从正态分布![]() (其中
(其中![]() 近似为平均数
近似为平均数![]() 近似为方差
近似为方差![]() ),则估计获表彰的学生人数为 .(四舍五入,保留整数)参考数据:随机变量
),则估计获表彰的学生人数为 .(四舍五入,保留整数)参考数据:随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() .
.
15.毛泽东思想是党的重要思想,某学校在团员活动中将四卷不同的《毛泽东选集》分发给三名同学,每个人至少分发一本,一共有种分发方法 .
16.已知函数![]() ,若
,若![]() 是函数
是函数![]() 的唯一极值点,则实数
的唯一极值点,则实数![]() 的取值范围是 .
的取值范围是 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
已知集合![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若存在正实数![]() ,使得“
,使得“![]() ”是“
”是“![]() ”成立的,求正实数
”成立的,求正实数![]() 的取值范围.
的取值范围.
从“(1)充分不必要条件,(2)必要不充分条件”中任选一个,填在上面空格处,补充完整该问题,并进行作答.
18.(本小题满分12分)
已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;(2)试讨论函数
处的切线方程;(2)试讨论函数![]() 的单调性.
的单调性.
19.(本小题满分12分)
某大学“爱牙协会”为了解“爱吃甜食”与青少年“蛀牙”情况之间的关系,随机对200名青少年展开了调查,得知这200个人中共有120个人“有蛀牙”,其中“不爱吃甜食”且“有蛀牙”的有30人,“不爱吃甜食”且“无蛀牙”的有50人.有![]() 列联表:
列联表:
| 有蛀牙 | 无蛀牙 | 总计 |
爱吃甜食 |
|
|
|
不爱吃甜食 |
|
|
|
总计 |
|
|
|
(1)根据已知条件完成如图所给的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“爱吃甜食”与青少年“蛀牙”有关;
的把握认为“爱吃甜食”与青少年“蛀牙”有关;
(2)若从“无蛀牙”的青少年中用分层抽样的方法随机抽取8人作进一步调查,再从这抽取的8人中随机抽取2人去担任“爱牙宣传志愿者”,求抽取的2人都是“不爱吃甜食”且“无蛀牙”的青少年的概率.附:![]() .
.
| 0.05 | 0.01 | 0.005 |
| 3.841 | 6.635 | 7.879 |
20.(本小题满分12分)
如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() 为线段
为线段![]() 的中点,
的中点,
![]() ,三棱锥
,三棱锥![]() 的体积为8.
的体积为8.
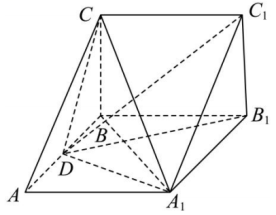
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 夹角的余弦值.
夹角的余弦值.
21.(本小题满分12分)
某篮球队为提高队员训练的积极性,进行小组投篮游戏;每个小组由两名队员组成,队员甲与队员乙组成一个小组.游戏规则如下:每个小组的两名队员在每轮游戏中分别投篮两次,每小组投进的次数之和不少于3次的称为“神投小组”,已知甲乙两名队员投进篮球的概率分别为![]() .
.
(1)若![]() ,求他们在第一轮游戏获得“神投小组”称号的概率;
,求他们在第一轮游戏获得“神投小组”称号的概率;
(2)已知![]() ,则:
,则:
①![]() 取何值时能使得甲、乙两名队员在一轮游戏中获得“神投小组”称号的概率最大?并求出此时的最大概率;
取何值时能使得甲、乙两名队员在一轮游戏中获得“神投小组”称号的概率最大?并求出此时的最大概率;
②在第(1)问的前提下,若甲、乙两名队员想要获得297次“神投小组”的称号,则他们平均要进行多少轮游戏?
22.(本小题满分12分)
已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设函数![]() 有两个极值点
有两个极值点![]() .
.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)证明:![]() .
.
2024届江苏省镇江中学高三上学期暑期学情检测数学试题含答案: 这是一份2024届江苏省镇江中学高三上学期暑期学情检测数学试题含答案,共21页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2024届江苏省镇江第一中学高三上学期期初学情检测数学试题含答案: 这是一份2024届江苏省镇江第一中学高三上学期期初学情检测数学试题含答案,共18页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
江苏省镇江地区2023-2024学年高三上学期期初检测开学考数学试卷: 这是一份江苏省镇江地区2023-2024学年高三上学期期初检测开学考数学试卷,文件包含数学试卷docx、数学答案docx等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。












