

四川省成都市石室中学2022-2023学年高三下学期二诊复习(文科)数学试题五
展开![]() 成都石室中学高2023届二诊复习题五(文科)
成都石室中学高2023届二诊复习题五(文科)
一、选择题(本题共12小题,每小题5分,在下列各题的四个选项中,只有一项符合题意的)
1. 已知集合![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 已知某公交车早晨![]() 点开始运营,每
点开始运营,每![]() 分钟发一班车,小张去首发站坐车,等车时间少于
分钟发一班车,小张去首发站坐车,等车时间少于![]() 分钟的概率为( )
分钟的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 若![]() 满足约束条件
满足约束条件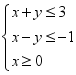 ,则
,则![]() 的最小值为( ) A. 1 B. 2 C. 3 D. 4
的最小值为( ) A. 1 B. 2 C. 3 D. 4
4. 下列说法正确的是( )
A 若
![]() ,则
,则![]()
B. “![]() ”是“函数
”是“函数![]() 是奇函数”的充要条件
是奇函数”的充要条件
C. ![]() ,都有
,都有![]()
D. ![]() 中,若
中,若![]() ,则
,则![]()
5. 已知![]() ,则
,则![]() 的值为( ) A.
的值为( ) A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 已知抛物线![]() 的焦点是F,点P的坐标为
的焦点是F,点P的坐标为![]() .若
.若![]() ,则a的值是( )
,则a的值是( )
A. 4 B. 3 C. 4或一4 D. 3或![]()
7.2022年9月16日,接迎第九批在韩中国人民志愿军烈士遗骸回国的运-20专机在两架歼-20战斗机护航下抵达沈阳国际机场.歼-20战斗机是我国自主研发的第五代制空战斗机,它具有高隐身性、高态势感知、高机动性能等特点,歼-20机身头部是一个圆锥形,这种圆锥的轴截面是一个边长约为2米的正三角形,则机身头部空间大约为( )
-
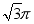 立方米 B.
立方米 B. 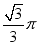 立方米 C.
立方米 C.  立方米 D.
立方米 D. 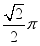 立方米
立方米
8定义在![]() 上的函数
上的函数![]() 满足
满足![]() 是偶函数,且
是偶函数,且![]() 若
若![]() ,则
,则![]() ( )
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9有甲、乙、丙、丁四位同学竞选班长,其中只有一位当选.有人走访了四位同学,甲说:“是乙或丙当选”,乙说:“甲、丙都未当选”,丙说:“我当选了”,丁说:“是乙当选了”,若四位同学的话只有两句是对的,则当选的同学是( ) A. 甲 B. 乙 C. 丙 D. 丁
10. 函数![]() 在区间
在区间![]() 上的所有零点之和等于( )
上的所有零点之和等于( )
A. ![]() B. 0 C. 3 D. 2
B. 0 C. 3 D. 2
11. 窗的运用是中式园林设计的重要组成部分,在表现方式上常常运用象征、隐喻、借景等手法,将民族文化与哲理融入其中,营造出广阔的审美意境.从窗的外形看,常见的有圆形、菱形、正六边形、正八边形等.已知圆O是某窗的平面图,O为圆心,点A在圆O的圆周上,点P是圆O内部一点,若![]() ,且
,且![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A. 3 B. 4 C. 9 D. 16
12.2022年9月钱塘江出现罕见潮景“鱼鳞潮”“鱼鳞潮”的形成需要两股涌潮,一股是波状涌潮,另外一股
是破碎的涌潮,两者相遇交叉就会形成像鱼鳞一样的涌潮.若波状涌潮的图象近似函数![]() 的图象,而破碎的涌潮的图象近似
的图象,而破碎的涌潮的图象近似![]() (
(![]() 是函数
是函数![]() 的导函数)的图象,已知当
的导函数)的图象,已知当![]() 时,两潮有一个交叉点,且破碎的涌潮的波谷为-4,有以下说法:
时,两潮有一个交叉点,且破碎的涌潮的波谷为-4,有以下说法:
①![]() ;②
;②![]() ;③
;③![]() 是偶函数;④
是偶函数;④![]() 在区间
在区间![]() 上单调,其中所有正确说法的个数为( )
上单调,其中所有正确说法的个数为( )
- 4 B. 3 C. 2 D. 1
二、填空题:(本题共4小题,每小题5分)
13. 复数z满足![]() ,(其中i为虚数单位),则
,(其中i为虚数单位),则![]() ______.
______.
- 已知直线
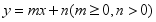 与圆
与圆 相切,则
相切,则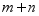 的取值范围是_____.
的取值范围是_____. - 已知圆台上底面半径为1,下底面半径为3,球与圆台的两个底面和侧面均相切,则该圆台的侧面积与球的表面积之比为________.
- 若
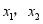 是函数
是函数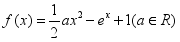 的两个极值点,且
的两个极值点,且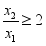 ,则实数
,则实数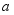 的取值范围为____.
的取值范围为____.
三、解答题:(共70分.解答写出文字说明,证明过程或演算步骤,第17-21题为必考题,每个试题考生都必须作答,第22,23为选考题,考生根据要求作答.)
17. 2021年6月17日9时22分,我国酒泉卫星发射中心用长征![]() 遥十二运载火箭,成功将神舟十二号载人飞船送入预定轨道,顺利将聂海胜、刘伯明、汤洪波3名航天员送入太空,发射取得圆满成功,这标志着中国人首次进入自己
遥十二运载火箭,成功将神舟十二号载人飞船送入预定轨道,顺利将聂海胜、刘伯明、汤洪波3名航天员送入太空,发射取得圆满成功,这标志着中国人首次进入自己空间站.某公司负责生产的A型材料是神舟十二号的重要零件,该材料应用前景十分广泛.该公司为了将A型材料更好地投入商用,拟对A型材料进行应用改造、根据市场调研与模拟,得到应用改造投入x(亿元)与产品的直接收益y(亿元)的数据统计如下:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
x | 2 | 3 | 4 | 6 | 8 | 10 | 13 | 21 | 22 | 23 | 24 | 25 |
y | 15 | 22 | 27 | 40 | 48 | 54 | 60 | 68.5 | 68 | 67.5 | 66 | 65 |
当![]() 时,建立了y与x的两个回归模型:模型①:
时,建立了y与x的两个回归模型:模型①:![]() ,模型②:
,模型②:![]() ;当
;当![]() 时,确定y与x满足的线性回归方程为
时,确定y与x满足的线性回归方程为![]() .
.
(1)根据下列表格中的数据,比较当![]() 时模型①,②的相关指数
时模型①,②的相关指数![]() 的大小,并选择拟合精度更高、更可靠的模型,预测对A型材料进行应用改造的投入为17亿元时的直接收益;
的大小,并选择拟合精度更高、更可靠的模型,预测对A型材料进行应用改造的投入为17亿元时的直接收益;
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 79.13 | 20.2 |
(2)为鼓励科技创新,当应用改造的投入不少于20亿元时,国家给予公司补贴5亿元,以回归方程为预测依据,根据(1)中选择的拟合精度更高更可靠的模型,比较投入17亿元与20亿元时公司收益(直接收益+国家补贴)的大小.
附: 刻画回归效果的相关指数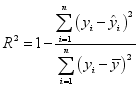 ,且当
,且当![]() 越大时,回归方程的拟合效果越好.用最小二乘法求线性回归方程
越大时,回归方程的拟合效果越好.用最小二乘法求线性回归方程![]() 的截距:
的截距:![]() .
.![]()
18. 已知数列![]() 满足
满足![]() ,
,![]() .
.
(1)证明:数列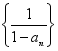 是等差数列,并求数列
是等差数列,并求数列![]() 的通项公式;
的通项公式;
(2)记![]() ,求
,求![]() 的前n项和
的前n项和![]()
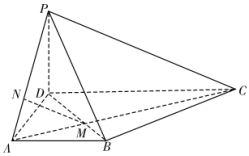 19. 在四棱锥
19. 在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() (
(![]() ),且
),且![]() 平面
平面![]() .
.
(I)求实数![]() 的值;
的值;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
20. 已知函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() .
.
(1)求实数![]()
取值范围,并讨论
![]() 的单调性;
的单调性;
(2)证明:![]() .
.
21. 已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)不与坐标轴垂直的直线![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求证:当
,求证:当![]() 的方向变化时,
的方向变化时,![]() 与
与![]() 的比值为常数.
的比值为常数.
选考题:共10分,请考生在第22,23题中任选一题作答,如果多做,则按所做第一题计分.
【选修4—4:极坐标与参数方程】
22. 在直角坐标系![]() 中,曲线
中,曲线![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() ,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上求一点P,使点P到直线
上求一点P,使点P到直线![]() 的距离最小.
的距离最小.
【选修4—5:不等式选讲】
23 已知函数
![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若![]() 在
在![]() 时有解,求实数a的取值范围.
时有解,求实数a的取值范围.
四川省成都市石室中学2022-2023学年高三数学下学期二诊复习(文科)试题七(Word版附答案): 这是一份四川省成都市石室中学2022-2023学年高三数学下学期二诊复习(文科)试题七(Word版附答案),共17页。试卷主要包含了已知复数z满足,则z的虚部是,已知集合,,则, 如图所示程序框图,其输出值, 已知双曲线,平面内三个单位向量满足,则A等内容,欢迎下载使用。
四川省成都市石室中学2022-2023学年高三数学下学期二诊复习(文科)试题三(Word版附答案): 这是一份四川省成都市石室中学2022-2023学年高三数学下学期二诊复习(文科)试题三(Word版附答案),共43页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
四川省成都市石室中学2022-2023学年高三下学期数学(文科)二诊复习题一: 这是一份四川省成都市石室中学2022-2023学年高三下学期数学(文科)二诊复习题一,共4页。试卷主要包含了抛物线的焦点坐标是,命题“”的否定命题是,设集合 则,已知,使用秦久韶算法计算,则,设 则,若,则,在中,下列说法正确的是等内容,欢迎下载使用。












