


初中数学华师大版八年级上册14.2 勾股定理的应用作业ppt课件
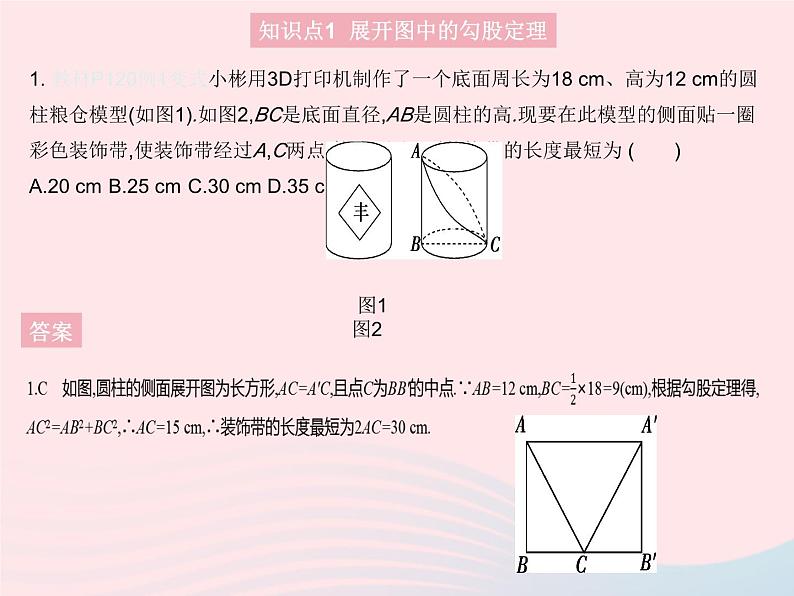
展开1. 教材P120例1变式小彬用3D打印机制作了一个底面周长为18 cm、高为12 cm的圆柱粮仓模型(如图1).如图2,BC是底面直径,AB是圆柱的高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为 ( )A.20 cmB.25 cmC.30 cmD.35 cm
知识点1 展开图中的勾股定理
图1 图2
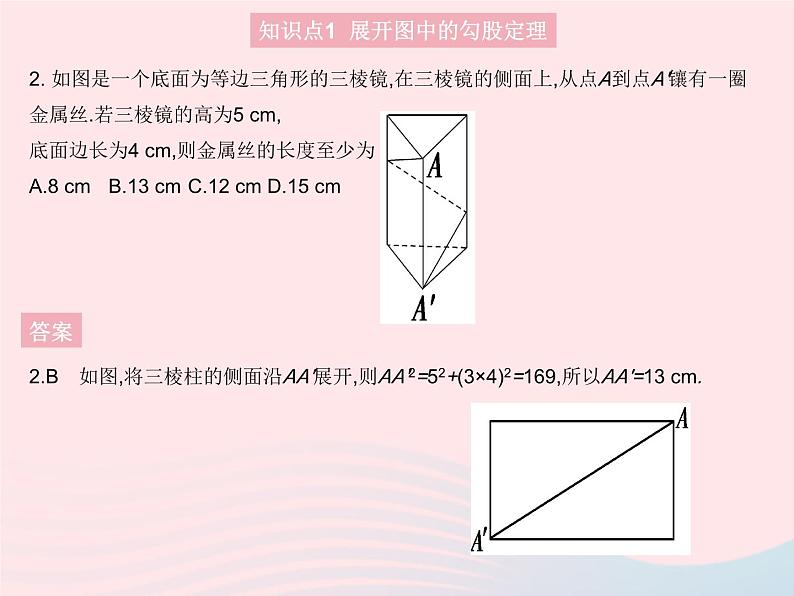
2. 如图是一个底面为等边三角形的三棱镜,在三棱镜的侧面上,从点A到点A'镶有一圈金属丝.若三棱镜的高为5 cm,底面边长为4 cm,则金属丝的长度至少为 ( )A.8 cmB.13 cmC.12 cmD.15 cm
2.B 如图,将三棱柱的侧面沿AA'展开,则AA'2=52+(3×4)2=169,所以AA'=13 cm.
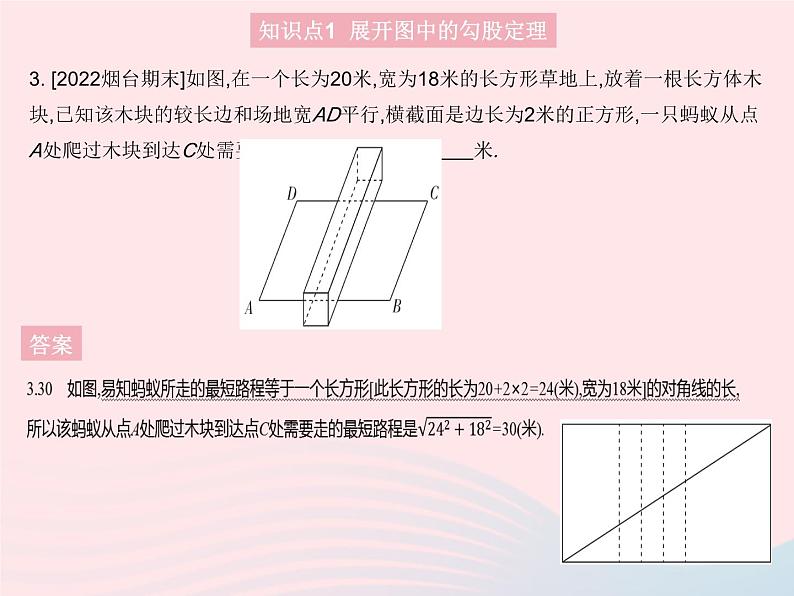
3. [2022烟台期末]如图,在一个长为20米,宽为18米的长方形草地上,放着一根长方体木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处爬过木块到达C处需要走的最短路程是 米.
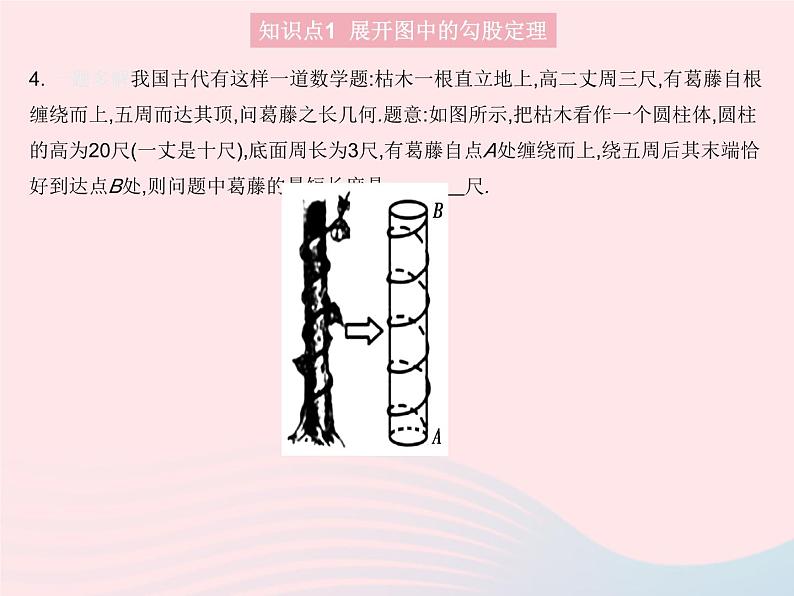
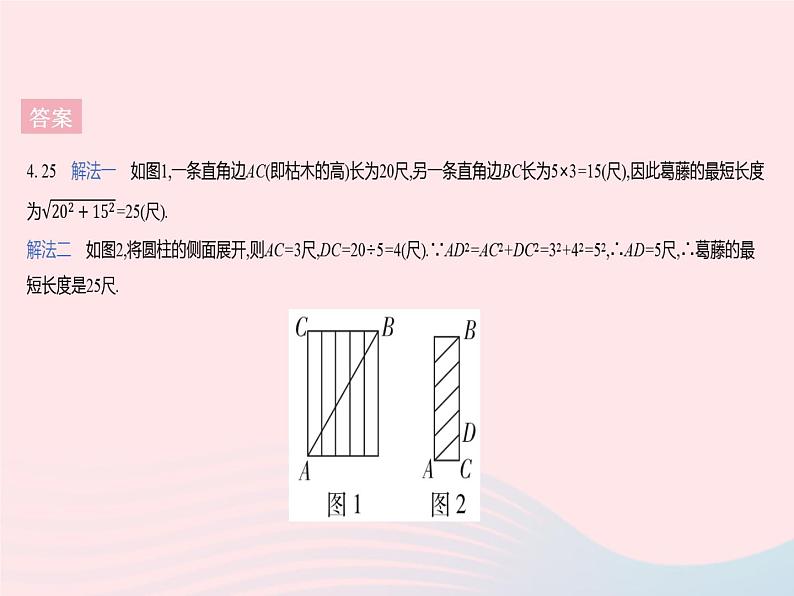
4. 一题多解我国古代有这样一道数学题:枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何.题意:如图所示,把枯木看作一个圆柱体,圆柱的高为20尺(一丈是十尺),底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是 尺.
5. [2021深圳南山区期末]小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度,于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面.则风筝距离地面的高度为 ( )A.6米 B.8米 C.10米 D.12米
5.D 如图,风筝在点A处,AB表示风筝距离地面的高度,AC表示风筝线.设AB=x米,则AC=(x+1)米.在Rt△ABC中,∠ABC=90°,BC=5米,则AB2+BC2=AC2,即x2+52=(x+1)2,解得x=12,所以风筝距离地面的高度为12米.
知识点2 实际应用中的勾股定理
6. 教材P126复习题T4变式如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为 米.
6.2.2 如图,在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,∴AB2=0.72+2.42=6.25.在Rt△A'BD中,∵∠A'DB=90°,A'D=2米,BD2+A'D2=A'B2,∴BD2+22=6.25,∴BD2=2.25,∴BD=1.5米,∴CD=BC+BD=0.7+1.5=2.2(米).
7. [2022青岛市南区期末]公路旁有一块山地正在开发,现有C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围250米内不得进入,在进行爆破时,公路AB段是否需要暂时封锁?请通过计算进行说明.
1. [2022洛阳期末]如图,已知钓鱼竿AC的长为10 m,露在水面上的线BC的长为6 m,某钓鱼者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的线B'C'的长为8 m,则BB'为 ( )A.1 mB.2 mC.3 mD.4 m
2. 如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点C,爬行的最短路线有( )A.3条B.4条C.6条D.12条
2.C 如图,若蚂蚁爬行时经过面AD,蚂蚁沿AD1 D1C(或AD2 D2C)爬行(其中D1,D2分别为其所在棱的中点)时,最短路线有2条;同理,若蚂蚁爬行时经过面AB,最短路线也有2条;若蚂蚁爬行时经过面AE,最短路线也有2条.因此,蚂蚁爬行的最短路线有6条.
3. [2021晋中期中]如图,某自动感应门的正上方A处装着一个感应器,离地2.5米,即AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则人头顶离感应器的距离AD为 米.
4. [2022沈阳苏家屯区期末]如图,长方体的长为3,宽为2,高为4,点B与点C之间的距离为1,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是 .
5. 小汽车在同方向划有两条以上机动车道的城市道路上,在没有限速标志、标线的情况下,最高速度不得超过70 km/h.如图,一辆小汽车自右向左在同方向划有两条以上机动车道的城市道路上直道行驶,某一时刻刚好行驶到路对面车速观察点A正前方30 m的C处,过了2.5 s后行驶到B处,此时测得小汽车与车速观察点A之间的距离为50 m,这辆小汽车超速了吗?
6. [2022衡阳期末]如图,某小区有两个喷泉A,B,两个喷泉的距离为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN为120 m,BM的长为150 m.(1)求从供水点M到喷泉A,B需要铺设的管道总长;(2)求喷泉B到小路AC的最短距离.
数学八年级上册14.2 勾股定理的应用作业ppt课件: 这是一份数学八年级上册14.2 勾股定理的应用作业ppt课件,共11页。
华师大版八年级上册14.2 勾股定理的应用课堂教学课件ppt: 这是一份华师大版八年级上册14.2 勾股定理的应用课堂教学课件ppt,文件包含第1课时勾股定理的应用1课件pptx、第2课时勾股定理的应用2课件ppt、习题142课件ppt等3份课件配套教学资源,其中PPT共44页, 欢迎下载使用。
数学14.2 勾股定理的应用教学课件ppt: 这是一份数学14.2 勾股定理的应用教学课件ppt,共26页。













