初中数学华师大版八年级上册1 全等三角形作业ppt课件

这是一份初中数学华师大版八年级上册1 全等三角形作业ppt课件，共14页。

1. 在△ABC中,AD,CE为高,两条高所在的直线相交于点H.若CH=AB,求∠ACB的度数.
1.解:∵AD,CE为△ABC的高,∴∠ADB=∠CEB=90°,∴∠BAD+∠B=90°,∠DCH+∠B=90°,∴∠DCH=∠DAB.在△ABD和△CHD中,∵∠DAB=∠DCH,∠ADB=∠CDH=90°,AB=CH,∴△ABD≌△CHD(),∴AD=CD.又∵∠ADC=90°,∴△ACD是等腰直角三角形,∴∠ACD=45°.
类型1　全等三角形问题中的分类讨论
如图1,当△ABC是锐角三角形时,∠ACB=45°;如图2,当△ABC是钝角三角形时,∠ACB=180°-∠ACD=180°-45°=135°.综上,∠ACB的大小为45°或135°.
2. 两个三角形的两边及其中一边上的高对应相等,这两个三角形是否全等?若全等,请给出证明;若不全等,请说明理由.
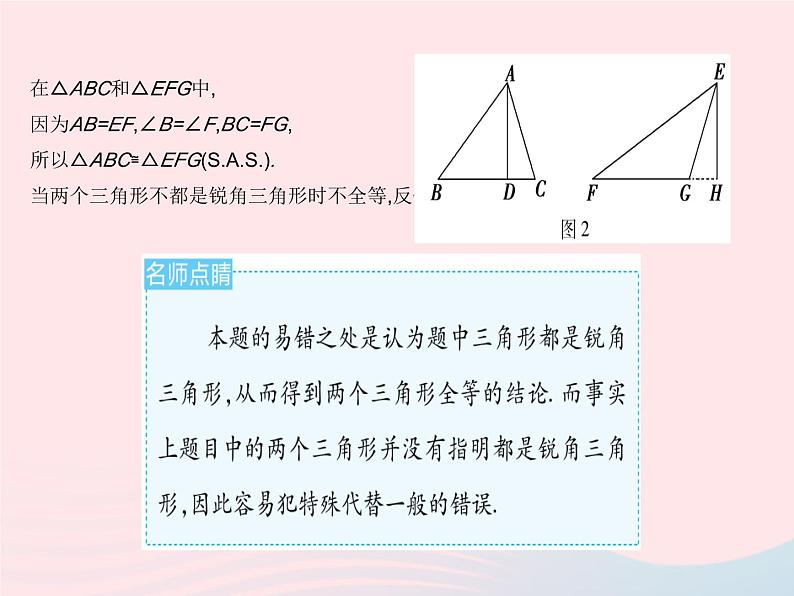
2.解:不一定全等.理由如下:当两个三角形均为锐角三角形或均为钝角三角形或均为直角三角形时全等.以两个三角形均为锐角三角形为例进行证明.(另外两种情况同理可证).已知:如图1,锐角三角形ABC和锐角三角形EFG中,AB=EF,BC=FG,AD⊥BC于点D,EH⊥FG于点H,且AD=EH.求证:△ABC≌△EFG.证明:因为AD⊥BC,EH⊥FG,所以∠ADB=∠EHF=90°.在Rt△ABD和Rt△EFH中,因为AB=EF,AD=EH,所以Rt△ABD≌Rt△EFH(H.L.),所以∠B=∠F.
在△ABC和△EFG中,因为AB=EF,∠B=∠F,BC=FG,所以△ABC≌△EFG().当两个三角形不都是锐角三角形时不全等,反例如图2.
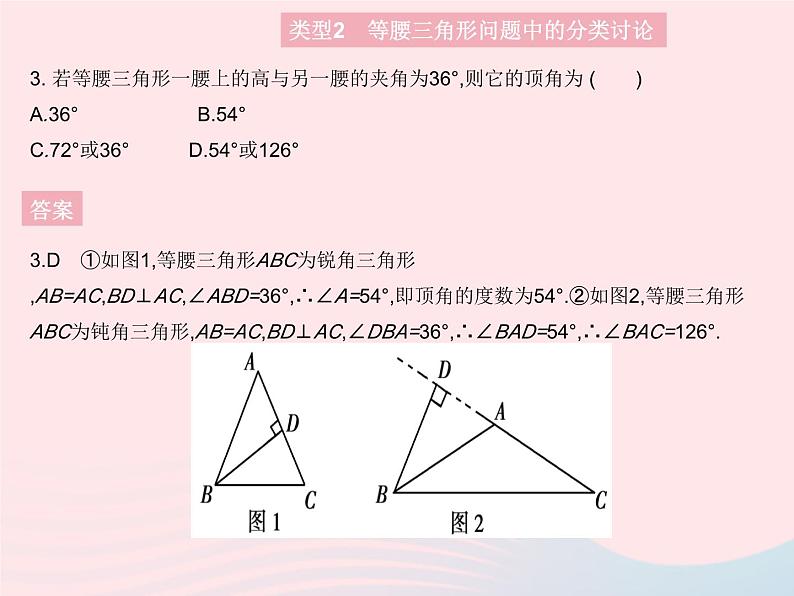
3. 若等腰三角形一腰上的高与另一腰的夹角为36°,则它的顶角为 (　　)A.36° B.54°C.72°或36°D.54°或126°
3.D　①如图1,等腰三角形ABC为锐角三角形,AB=AC,BD⊥AC,∠ABD=36°,∴∠A=54°,即顶角的度数为54°.②如图2,等腰三角形ABC为钝角三角形,AB=AC,BD⊥AC,∠DBA=36°,∴∠BAD=54°,∴∠BAC=126°.
类型2　等腰三角形问题中的分类讨论
4. 在△ABC中,AB=AC,AB的垂直平分线与边AC所在的直线相交所得的锐角为50°,求∠C的度数.
5. 在△ABC中,AB=AC.若OB=OC,点A到BC的距离是6,点O到BC的距离是4,则AO= (　　)A.2　　B.8或10　　C.2或10　　D.8
5.C　∵ AB=AC,OB=OC,∴ A,O都在线段BC的垂直平分线上,设该垂直平分线与BC交于点M,则AM⊥BC.∵点A到BC的距离为6,点O到BC的距离为4,∴AM=6,OM=4.分两种情况讨论:①点O在△ABC内,此时AO=AM-OM=2;②点O在△ABC外,此时 AO=AM+OM=10.
类型3　线段垂直平分线与角平分线问题中的分类讨论
6. 在△ABC中,∠ABC=60°,∠ACB=70°.若点O到△ABC三边的距离相等,求∠BOC的度数.