华师大版八年级上册1 全等三角形作业课件ppt

这是一份华师大版八年级上册1 全等三角形作业课件ppt，共11页。

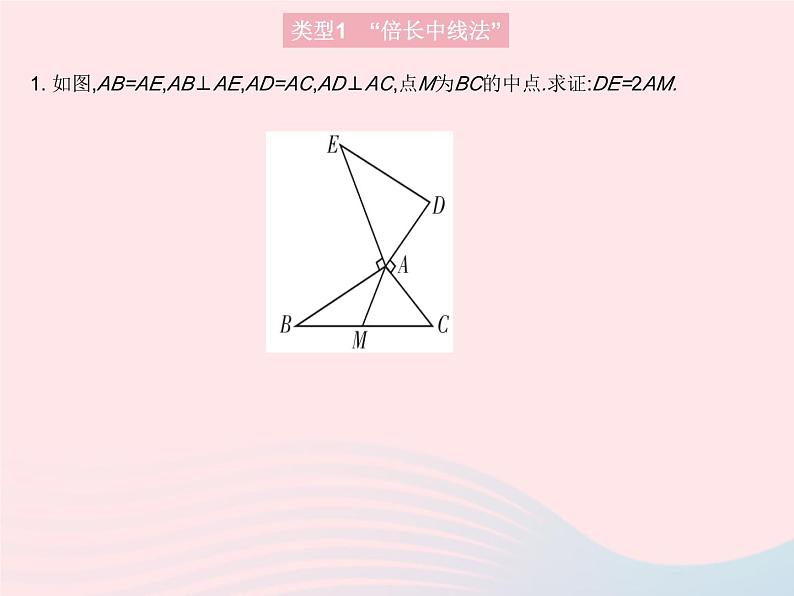
1. 如图,AB=AE,AB⊥AE,AD=AC,AD⊥AC,点M为BC的中点.求证:DE=2AM.
类型1　“倍长中线法”
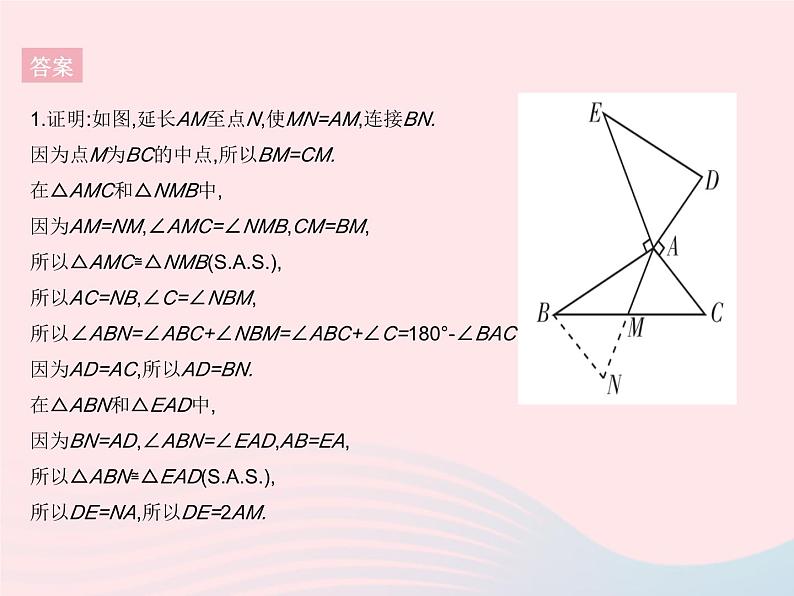
1.证明:如图,延长AM至点N,使MN=AM,连接BN.因为点M为BC的中点,所以BM=CM.在△AMC和△NMB中,因为AM=NM,∠AMC=∠NMB,CM=BM,所以△AMC≌△NMB(),所以AC=NB,∠C=∠NBM,所以∠ABN=∠ABC+∠NBM=∠ABC+∠C=180°-∠BAC=∠EAD.因为AD=AC,所以AD=BN.在△ABN和△EAD中,因为BN=AD,∠ABN=∠EAD,AB=EA,所以△ABN≌△EAD(),所以DE=NA,所以DE=2AM.
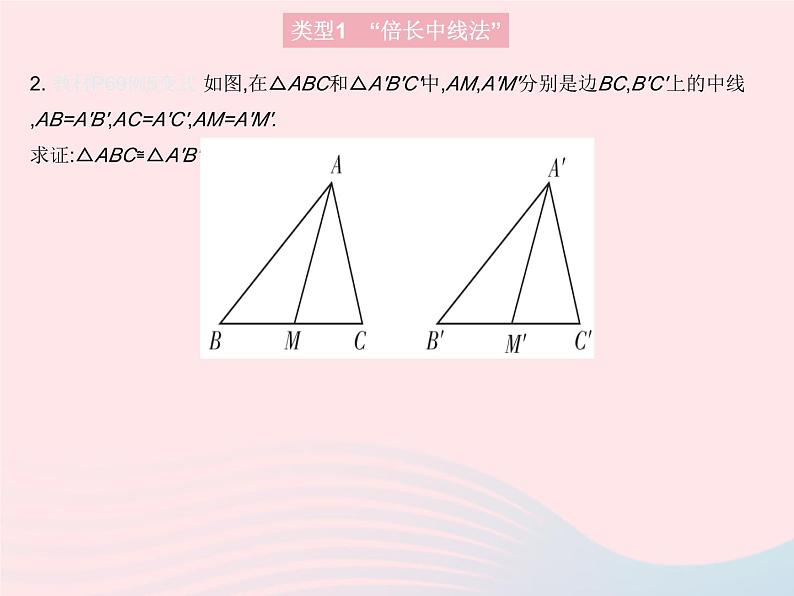
2. 教材P69例5变式 如图,在△ABC和△A'B'C'中,AM,A'M'分别是边BC,B'C'上的中线,AB=A'B',AC=A'C',AM=A'M'.求证:△ABC≌△A'B'C'.
2.证明:如图,分别延长AM和A'M'到点E和E',使ME=AM,M'E'=A'M',连接BE,B'E'.因为AM,A'M'分别是边BC,B'C'上的中线,所以BM=CM,B'M'=C'M'.在△AMC和△EMB中,因为AM=EM,∠AMC=∠EMB,CM=BM,所以△AMC≌△EMB(),所以BE=AC,∠MAC=∠E.同理,可得△A'M'C'≌△E'M'B',所以B'E'=A'C',∠M'A'C'=∠E'.因为AC=A'C',所以BE=B'E'.因为AE=2AM,A'E'=2A'M',且AM=A'M',所以AE=A'E'.
在△ABE和△A'B'E'中,因为AE=A'E',BE=B'E',AB=A'B',所以△ABE≌△A'B'E'(),所以∠BAE=∠B'A'E',∠E=∠E',所以∠MAC=∠M'A'C',所以∠BAC=∠B'A'C'.在△ABC和△A'B'C'中,因为AB=A'B',∠BAC=∠B'A'C',AC=A'C',所以△ABC≌△A'B'C'().
3. 如图,在△ABC中,AB>AC,∠1=∠2,P为AD上任意一点.求证:AB-AC>PB-PC.
类型2　“截长补短法”
3.证明:如图,延长AC至点M,使AM=AB,连接PM.在△ABP和△AMP中,因为AB=AM,∠1=∠2,AP=AP,所以△ABP≌△AMP(),所以PB=PM.在△PCM中,根据三角形的三边关系,得CM>PM-PC,所以AM-AC>PB-PC,所以AB-AC>PB-PC.
4. [2021广州期中]如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,点E在AD上.求证:BC=AB+CD.
4.证明:如图,在BC上截取BF=AB,连接EF.因为∠ABC,∠BCD的平分线交于点E,所以∠ABE=∠FBE,∠FCE=∠DCE.在△ABE和△FBE中,因为AB=FB,∠ABE=∠FBE,BE=BE,所以△ABE≌△FBE(),所以∠A=∠BFE.因为AB∥CD,所以∠A+∠D=180°,所以∠BFE+∠D=180°.因为∠BFE+∠CFE=180°,所以∠CFE=∠D.在△FCE和△DCE中,