初中数学1 全等三角形课前预习课件ppt

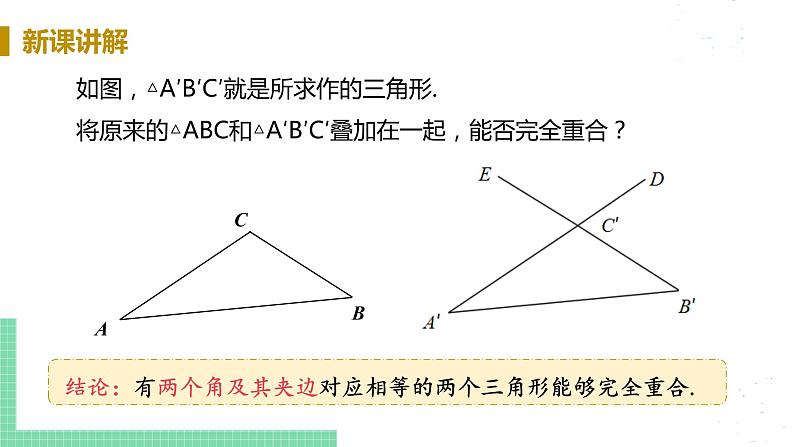
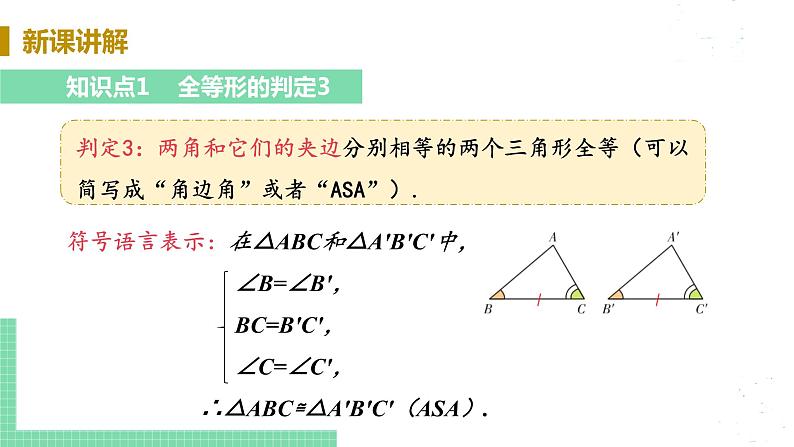
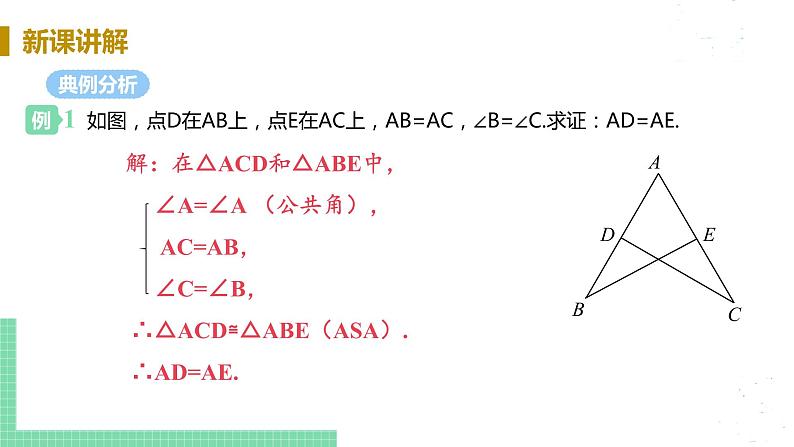
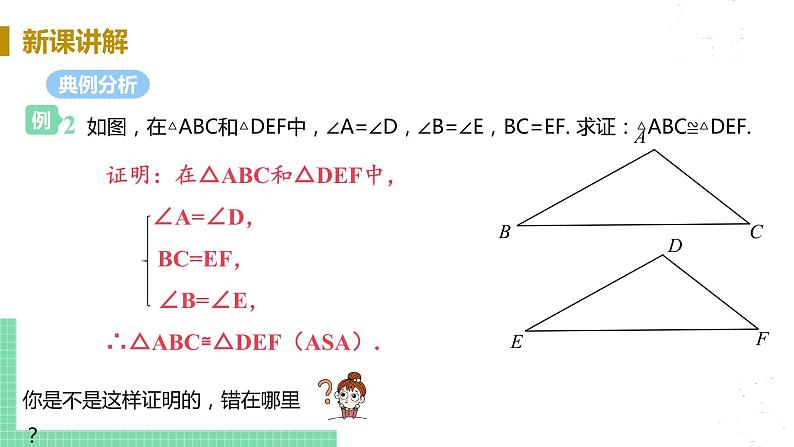
13.2三角形全等的判定

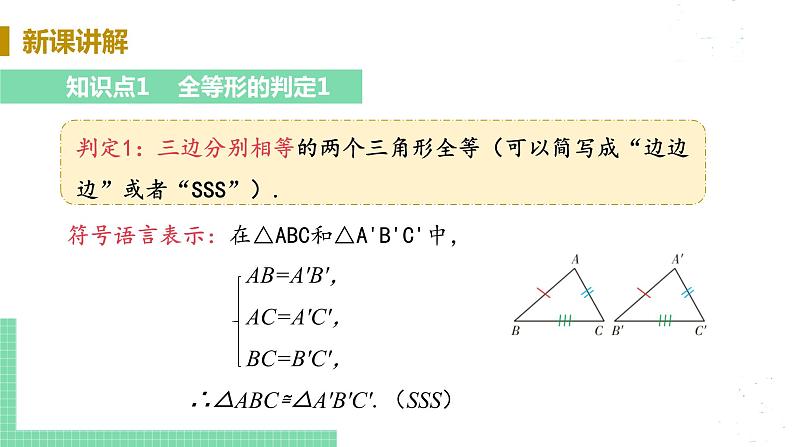
1．如图，在△ABC和△DEC中，已知AB＝DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（    ）

A．BC＝EC，∠B＝∠E

B．BC＝EC，AC＝DC

C．BC＝DC，∠A＝∠D

D．∠B＝∠E，∠A＝∠D

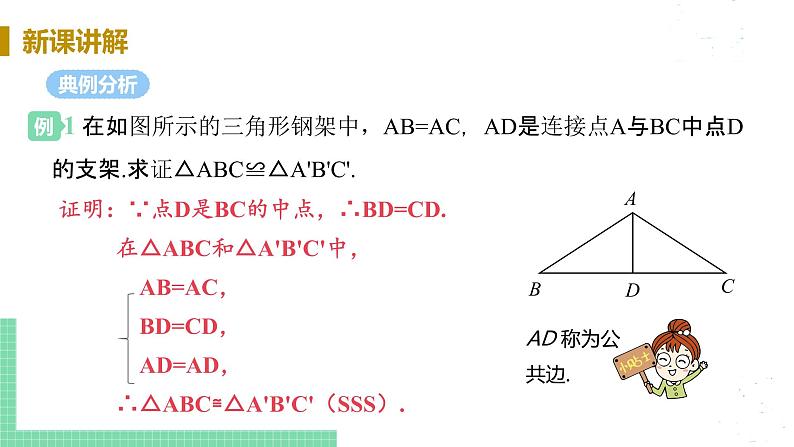
2．如图所示，已知：点B、F、C、E在一条直线上，FB＝CE，AC＝DF.能否由上面的已知条件证明AB∥ED?如果能，请给出证明；如果不能，请从下列四个条件中选择一个合适的条件，添加到已知条件中，使AB∥ED成立，并给出证明．供选择的四个条件：

①AB＝DE;②∠A＝∠D＝90°；③∠ACB＝∠DFE;④∠A＝∠D．

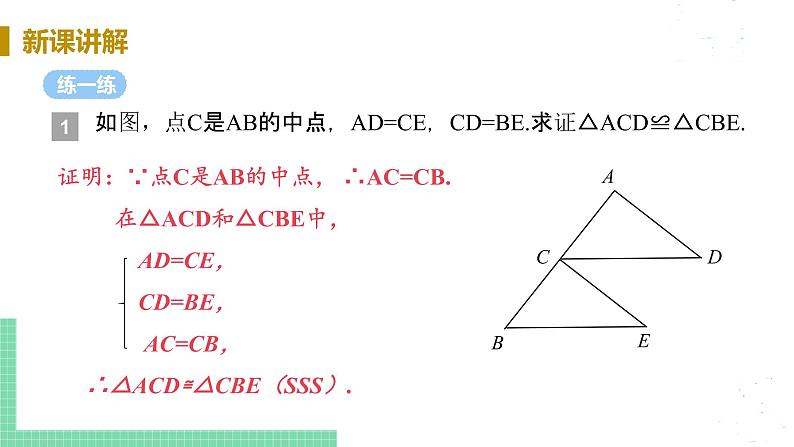
3．如图所示，△ABC是等边三角形，D是AB上一点，以CD为边作等边三角形CDE，使点E，A在直线CD的同侧，连接AE.求证：AE∥BC.

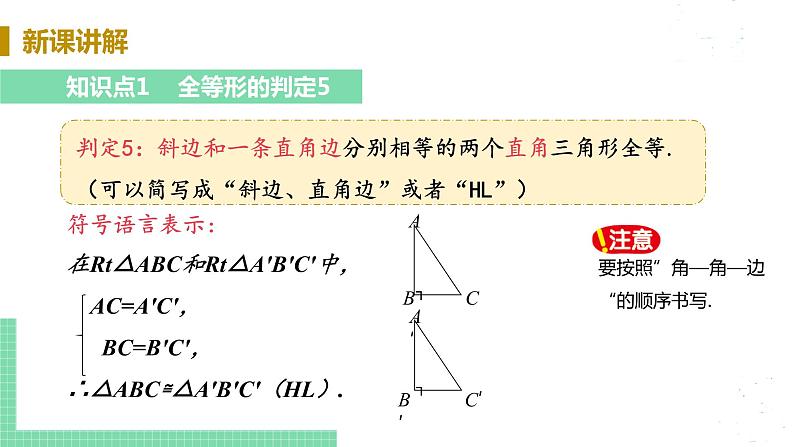
4．如图所示，在△AOB和△COD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝90°，当将△COD绕点O顺时针旋转时，连线AC与BD之间的大小关系如何？试猜想并证明你的结论.

5．如图所示，已知BD＝CE，AB＝FD，B，D，C，E共线．若添加一个条件，就能使△ABC≌△FDE，则下列条件中满足的个数为（    ）

①AB∥DF;②AC∥EF;③∠A＝∠F;④∠A＝∠F＝90°．

A．1  B．2  C．3  D．4

6．如图所示，∠E＝∠F，∠B＝∠C，AE＝AF，以下结论：①∠FAN＝∠EAM;②EM＝FN；③△ACN≌△ABM；④CD＝DN其中正确的有（    ）

A．1个  B．2个  C．3个  D．4个

7．如图，直线l过正方形ABCD的顶点B，点A，C到直线l的距离分别是AE＝1，CF＝2，则EF＝________．

8．如图所示，∠B＝∠D，BC＝DC，要判定△ABC≌△EDC，当添加条件________时，可根据“ASA”判定；当添加条件________时，可根据“AAS”判定；当添加条件________时，可根据“SAS”判定．

9．如图所示，已知AB∥CD，OA＝OD，AE＝DF.请说明EB∥CF．

10．如图所示，∠B＝∠D，请在不添加辅助线的情况下，添加一个适当的条件，使△ABC≌△ADE并证明．

（1）添加的条件是________．

（2）证明：△ABC≌△ADE．

11.．如图（1），OA＝2，OB＝4，以A为顶点，AB为腰在第三象限作等腰直角三角形ABC.

（1）求C点的坐标；

（2）如图（2），P为y轴负半轴上一个动点，当点P沿y轴负半轴向下运动时，以P为顶点，PA为腰作等腰直角三角形APD，过点D作DE⊥x轴于点E，求OP－DE的值．

12．如图（1）所示，已知在△ABC中，∠BAC＝90°，AB＝AC，AE是过点A的一条直线，且B点和C点在AE的异侧，BD⊥AE于D点，CE⊥AE于E点．

（1）求证：BD＝DE+CE.

（2）若直线AE绕点A旋转到图（2）所示的位置时（BD<CE），其余条件不变，问BD与DE，CE的关系如何？请予以证明．

（3）若直线AE绕点A旋转到图（3）所示的位置时（BD>CE），其余条件不变，问BD与DE，CE的关系如何？直接写出结果，不需证明．

13．如图，AM∥BN，∠MAB，∠NBA的平分线交于C点，过C作一直线交AM于D，交BN于E.

求证：AB＝AD+BE.

14．问题背景：

如图，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°.E，F分别是BC，CD上的点，且∠EAF＝60°．探究图中线段BE，EF，FD之间的数量关系，

小王同学探究此问题的方法是，延长FD到点G，使DG＝BE.连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是________.

15.探索延伸：

如图，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是BC，CD上的点，且，上述结论是否仍然成立？并说明理由.

16.实际应用：

如图，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里／时的速度前进，舰艇乙沿北偏东50°的方向以80海里／时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．

参考答案

1．C

2．解：不能。

选择条件①（还可选择②或③），但不能选择条件④）。

证明如下：，，即。

在和中，

，，。

3．分析：根据等边三角形的三边相等，三个角相等，推出，，，进而得出，从而根据“”证出，可得，进而得出。

证明：因为和是等边三角形，

所以，，。

所以。

在和中

所以。

所以。

所以。

4．思路建立，可知，要说明，可考虑证明，所在三角形全等。但当绕点顺时针旋转时可出现，不分别与，重合；，分别与，在同一直线上；、分别在，上三种情况，故要分类讨论。

解：。   

证明过程如下：

①当连线，不分别与，重合时，

，，即。

在和中，

，。

②当连线，分别与，在同一直线上时，如图，

。

③当连线，分别在，上时，如图，

。

综合以上三种情况可知。

5．B  解析 由可得到，又因为，所以当，即时，能使，当时，根据“HL”可得，又易知添加②或③不能使，故选B。

6．C  解析 在和中，，，，①正确。在和中，，，，②正确。在和中，，③正确，④不正确。正确的结论有3个，故选C。

7．3  解析 因为，，所以。又因为，，所以。所以，，即。

8．（也可以是）；；  解析，，要判定，根据“ASA”可添加（或），根据“AAS”可添加；根据“SAS”可添加。

9．分析：由条件可得出，所以，进一步可得，所以，所以。

解：如图D-12-2，因为，所以，

所以（等角的补角相等）。

在和中，，，

所以，所以。

在和中，，，，

所以，

所以。

所以（内错角相等，两直线平行）。

方法：利用全等三角形得出两角相等后，还可以进一步得到两直线平行、两直线垂直等。这类问题综合性较强，往往需要结合直线平行的性质与判定、垂直的性质与判定等，解题时要认真分析题目所给的条件与图形特征，选择合理、简捷的方法。

10．分析：由图形可观察到和有公共角，即，又已知。因此添加和中任意一组对应边相等均可证出两个三角形全等。

解：方法1：（1）添加的条件是。

（2）证明：在和中，

所以。

方法2：（1）添加的条件是。

（2）证明：在和中，

所以。

方法3：（1）添加的条件是：。

（2）证明：在和中，

所以。

11．思路建立，（1）要求点C的坐标，就需要过点C作x轴的垂线CF，然后求CF，OF的长，而已知，，为等腰直角三角形，，故可考虑证明。

（2）要求的值，而与的长不易求，故考虑将，转化到同一条直线上。因此需要过点作轴交延长线于点，然后，使，则。

解：（1）过点作轴与点。

。

。

又，。

。

在和中，

，，。

，，，。

又点C在第三象限，点的坐标为。

（2）过点作轴交的延长线于点。

，

，，。

轴，，，。

，。

又，。。

。

12．思路建立，在（1）中，观察图形易得。而要求证的结论是。若，则容易得到结论，而证明可由条件，及证得。而（2）（3）中结论的探索，则完全可借助于图形，再根据（1）中条件得结论。

（1）证明： 于，于，

。

，。

，

。

在和中，

，，。

，。

（2）解：。

证明如下：于，∴。

，，

。

在和中，

∴，，，

∴。

（3）略

13．思路建立，要证明，可采用“截长法”，将线段分成两段，使得其中一段与相等，另一段与相等。故在上截取，然后证明即可。

证明：在上截取，连接，

如图，

在和中，

所以，所以。

又因为，所以。

而，所以。

在和中，

所以，所以。

又因为，所以。

点拨：证明一条线段等于两条线段的和，可采用“截长法”或“补短法”，“截长法”的基本思路是在长线段上截取一段，使之等于其中一短线段，然后再证明剩下的线段等于另一短线段。“补短法”的基本思路是延长短线段，使延长的部分等于另一短线段，再证明延长后的线段等于长线段。

14．分析：问题背景：根据全等三角形对应边相等解答。

探索延伸：延长到，使，连接，根据同角的补角相等求出，然后利用“边角边”证明和全等，根据全等三角形对应边相等可得，，再求出，然后利用“边角边”证明和全等，根据全等三角形对应边相等可得，然后求解即可。

15.实际应用：连接，延长，相较于点，然后求出，判断出符合探索延伸的条件，再根据探索延伸的结论解答即可。

解：问题背景：。

探索延伸：仍然成立。

理由如下：

如图，延长到，使，连接。

，，

。

在和中，

，。

，，

。

在和中，

，。

，。

16.实际应用：如图D-12-7，连接，延长，相较于点。，，

。

又，，

符合探索延伸中的条件，结论成立，即（海里）。答：此时两舰艇之间的距离是210海里。

点拨：本题考查了全等三角形的判定与性质，读懂问题背景的求解思路，作辅助线构造出全等三角形并两次证明三角形全等是解题的关键，也是本题的难点。