初中数学北师大版九年级上册1 成比例线段精品第1课时教案

第四章 图形的相似

1 成比例线段

第1课时 线段的比和比例的基本性质

【知识与技能】

1.通过简单实例了解两条线段的比的概念.

2.了解比例的基本性质及应用.

【过程与方法】

经历探索成比例线段的过程，并利用其解决一些简单的问题.

【情感态度】

通过现实情境，培养应用意识，了解数学、自然、社会的密切联系.

【教学重点】

成比例线段的基本性质.

【教学难点】

成比例线段的基本性质.

一、情境导入，初步认识

请写出线段AB和CD的比，并讨论线段的比有哪些地方是需要特别留意的？

【教学说明】让学生初步了解线段的比就是线段长度的比.

让学生在两个实例中理解线段的比要注意以下几点：

1.线段的比是正数

2.单位要统一

3.线段的比与线段的长度无关

二、思考探究，获取新知

1.由下面的格点图可知，=_______，=_______，这样与之间有关系_______.

【归纳结论】对于四条线段a、b、c、d，如果其中两条线段的长度的比等于另外两条线段的比，如=（或a∶b＝c∶d），那么，这四条线段叫做成比例线段，简称比例线段.此时也称这四条线段成比例.

【教学说明】从具体的事例中感受线段的成比例.

 2.如果四条线段a、b、c、d成比例，即.那么ad＝bc吗？如果ad＝bc，那么a、b、c、d成比例吗？

【归纳结论】如果，那么ad=bc.如果ad=bc（a、b、c、d都不等于0），那么.

【教学说明】培养学生的自学能力及归纳能力.

三、运用新知，深化理解

1.一条线段的长度是另一条线段的3倍，则这两条线段的比为3∶1.

2.已知3x=4y，则=.

3.已知四条线段a、b、c、d的长度，试判断它们是否成比例？

（1）a=16cm       b=8cm        c=5cm       d=10cm;

（2）a=8cm        b=5cm        c=6cm         d=10cm.

分析：（1）=2，=2，则=，所以a、b、d、c成比例.

（2）由已知得ab≠cd，ac≠bd，ad≠bc，所以a、b、c、d四条线段不成比例.

4.在比例尺为1∶200的地图上，测得A，B两地间的图上距离为4.5cm，求A，B两地间的实际距离.

分析：利用比例尺的定义即“”列出等量关系式.

解：设A、B两地间的实际距离为xcm，则.解得x=900.

∴设A、B两地间的实际距离为900cm.

5.已知a、b、c、d是成比例线段，且a=3cm，b=2cm，c=6cm，求线段d的长.

分析：由a、b、c、d是成比例线段得，代入计算求出线段d的长.

解：∵a、b、c、d是成比例线段，

∴，即.

解得d=4cm.

6.已知三条线段的长分别为2、4、8，请你再添上一条线段，使它们成比例，求出所有符合条件的线段长.

分析：

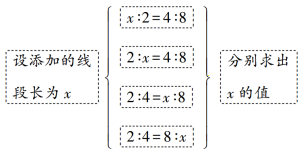
解：设添加的线段长为x，

当x≤2时，x∶2=4∶8，x=1;

当2≤x≤4时，2∶x=4∶8，x=4;

当4≤x≤8时，2∶4=x∶8，x=4;

当x≥8时，2∶4=8∶x，x=16.

综上，符合条件的线段长可为：1，4，16.

【教学说明】本题运用了分类讨论思想求解，解题的关键是找出各种可能的情况.先设要添加的线段长为x，然后使这四个数各自成比例，再算出x的值.

四、师生互动，课堂小结

1.本节课你有哪些收获？

2.通过这节课的学习，你还存在哪些疑惑？

【教学说明】让学生相互交流后，单独回答、提问.

1.布置作业:教材“习题4.1”中第1  题.

2.完成练习册中相应练习.

本节的重点是线段的比和比例线段的概念以及比例的性质.虽然小学时已经接触过比例性质的一些知识，但内容比较简单，而本节涉及到的比例基本性质变式较多，容易混淆.所以应多加训练.