2023九年级数学下册第27章圆27.1圆的认识课时3垂径定理作业课件新版华东师大版

这是一份2023九年级数学下册第27章圆27.1圆的认识课时3垂径定理作业课件新版华东师大版，共21页。

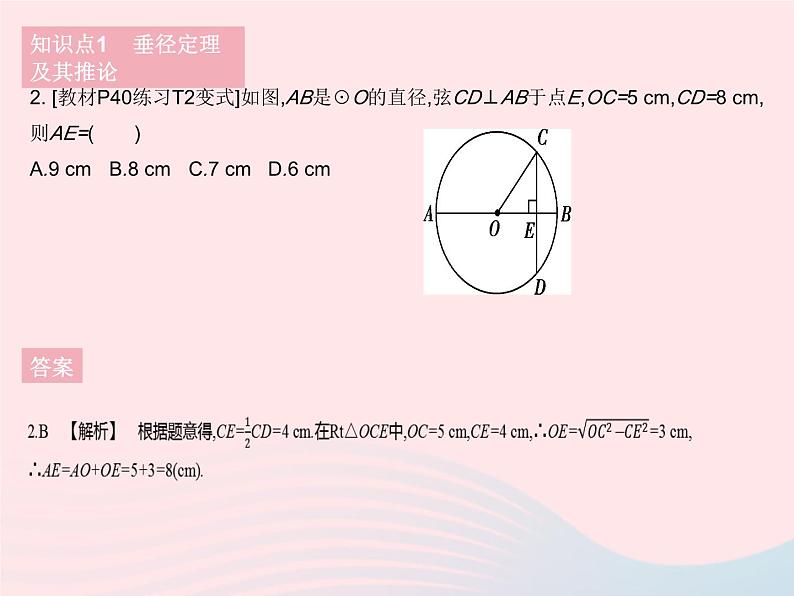
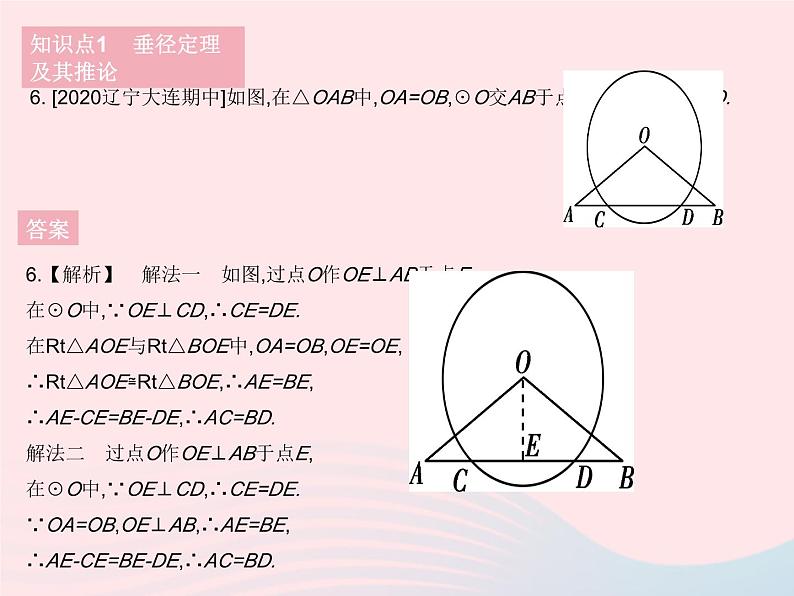
※课时3　垂径定理1. 易错题 给出下列说法:①平分弧的直径垂直平分弧所对的弦;②平分弦的直径平分弦所对的弧;③垂直于弦的直线必过圆心;④垂直于弦的直径平分弦所对的弧.其中正确的是 (　　)A.②③ B.①③ C.②④ D.①④知识点1 垂径定理及其推论答案1.D　【解析】　平分弦(不是直径)的直径平分弦所对的弧,故②错误;垂直于弦且平分弦的直线必过圆心,故③错误;易知①④正确.2. [教材P40练习T2变式]如图,AB是☉O的直径,弦CD⊥AB于点E,OC=5 cm,CD=8 cm,则AE=(　　)A.9 cm B.8 cm C.7 cm D.6 cm知识点1 垂径定理及其推论答案  知识点1 垂径定理及其推论答案 4. 如图,点A,B是☉O上两点,AB=10,点P是☉O上的一个动点(点P与点A,B不重合),连接AP,PB,过点O分别作OE⊥AP于点E,OF⊥PB于点F,则EF的长为　　　　. 知识点1 垂径定理及其推论答案  知识点1 垂径定理及其推论答案 6. [2020辽宁大连期中]如图,在△OAB中,OA=OB,☉O交AB于点C,D.求证:AC=BD.知识点1 垂径定理及其推论答案6.【解析】　解法一　如图,过点O作OE⊥AB于点E.在☉O中,∵OE⊥CD,∴CE=DE.在Rt△AOE与Rt△BOE中,OA=OB,OE=OE,∴Rt△AOE≌Rt△BOE,∴AE=BE,∴AE-CE=BE-DE,∴AC=BD.解法二　过点O作OE⊥AB于点E,在☉O中,∵OE⊥CD,∴CE=DE.∵OA=OB,OE⊥AB,∴AE=BE,∴AE-CE=BE-DE,∴AC=BD.7. 如图,在半径为13 cm的圆形铁片上切下一块高为8 cm的弓形铁片,则弓形的弦AB的长为 (　　)A.10 cm B.16 cm C.24 cm D.25 cm知识点2 垂径定理的实际应用答案 8. [2021山东淄博中考]“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD为☉O的直径,弦AB⊥CD,垂足为点E,CE=1寸,AB=10寸,则直径CD的长度是 (　　)A.12寸 B.24寸 C.13寸 D.26寸知识点2 垂径定理的实际应用答案8.D　【解析】　连接OA.∵AB⊥CD,且AB=10寸,∴AE=BE=5寸.设☉O的半径OA的长为x寸,则OC=OD=x寸.∵CE=1寸,∴OE=(x-1)寸.在Rt△AOE中,根据勾股定理得,x2-(x-1)2=52,化简得2x=26,∴CD=26寸.9. [2021北京丰台区期中]如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端AB=1.8米,C为AB的中点,D为拱门最高点,圆心O在线段CD上,CD=2.7米,求拱门所在圆的半径长.知识点2 垂径定理的实际应用答案 1. [2021河北承德一模]如图,☉O的直径为10,弦AB的长为6,P为弦AB上的动点,则线段OP长度的取值范围是 (　　)A.3≤OP≤5 B.4