广东省广州市2022-2023学年下学期八年级数学期末综合练习（二）

2022-2023学年人教版8年级下册数学期末综合练习（二）

一．选择题（共10小题）

1．要使在实数范围内有意义，则x的取值范围是（　　）

A．x≤1 B．x＞1 C．x≥0 D．x≥1

2．满足下列条件时，△ABC不是直角三角形的是（　　）

A．∠A：∠B：∠C＝3：4：5 B．AB：BC：AC＝3：4：5 

C．AB，BC＝4，AC＝5 D．∠A＝40°，∠B＝50°

3．在平行四边形ABCD中，∠A＝80°，∠B＝100°，则∠D等于（　　）

A．60° B．80° C．100° D．120°

4．一次函数y＝﹣2x+6的图象与y轴的交点坐标是（　　）

A．（0，6） B．（6，0） C．（3，0） D．（0，3）

5．下列运算正确的是（　　）

A．     B．  C．   D．

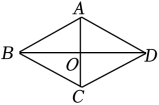
6．如图，▱ABCD的对角线AC与BD相交于点O，添加下列条件不能证明▱ABCD是菱形的是（　　）

A．∠ABD＝∠ADB B．AC⊥BD C．AB＝BC D．AC＝BD

     第6题图                  第7题图                     第9题图

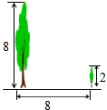
7．如图，有两棵树，一棵高8米，另一棵高2米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，则它至少要飞行（　　）米．

A．6 B．8 C．10 D．12

8．已知一次函数y＝﹣x+2，那么下列结论正确的是（　　）

A．y的值随x的值增大而增大            B．图象经过第一、二、三象限 

C．图象必经过点（0，2）                D．当x＜2时，y＜0

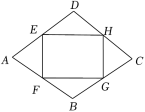
9．如图，四边形ABCD为菱形，AB＝6，∠A＝60°，连接四边中点得到四边形EFGH，则四边形EFGH的面积为（　　）

A．9 B．6 C．18 D．9

10．为计算某样本数据的方差，列出如下算式S2，据此判断下列说法错误的是（　　）

A．样本容量是4 B．样本的平均数是4 

C．样本的众数是3 D．样本的中位数是3

二．填空题（共6小题，每题3分，共18分）

11．化简：　      　．

12．命题“直角三角形两条直角边的平方和等于斜边的平方”的逆命题是　                  　．

13．一组数据：1、2、4、3、2、4、2、5、6、1，它们的中位数为　      　．

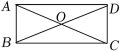
14．如图，矩形ABCD的对角线AC，BD相交于点O，若∠AOB＝50°，则∠OBC的度数是 　     　度．

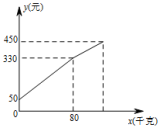
15．一水果商贩在批发市场按1.8元/千克批发了若干千克的苹果进城出售，为了方便，他带了一些零钱备用，他先按市场价出售一些后，又每千克下降0.5元将剩余的苹果降价售完，这时他手中的钱（含备用零钱）是450元．售出苹果x千克与他手中持有的钱数y元（含备用零钱）的关系如图所示，则这个水果商贩一共赚　      　元．

        第15题图                          第16题图

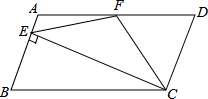
16．如图，在▱ABCD中，AD＝2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是　      　．（把所有正确结论的序号都填在横线上）

①∠DCF∠BCD；②EF＝CF；③S△BEC＝2S△CEF；④∠DFE＝3∠AEF．

三．解答题（17-19题每题6分，20-22题每题8分，23-25题每题10分）

17．计算：．

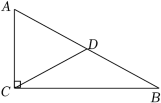
18．在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，D是AB的中点，求CD的长．

19．为深入学习贯彻习近平法治思想，推动青少年宪法学习宣传教育走深走实，教育部组织开展第七届全国学生“学宪法讲宪法”系列活动．某校积极响应教育部的号召，开展了宪法知识在线学习、知识竞赛与演讲比赛三项活动．如表是参加冠亚军决赛的两名选手的综合测评成绩单（单位：分）．

（1）若将在线学习、知识竞赛与演讲比赛三项成绩的平均分作为最后成绩，谁将会获得冠军？

（2）若将在线学习、知识竞赛与演讲比赛按2：3：5的比例计算最后成绩，谁将会获得冠军？

20．如图，在四边形ABCD中，AC与BD相交于点O，且AO＝CO，点E在BD上，满足∠EAO＝∠DCO．

（1）求证：四边形AECD是平行四边形；

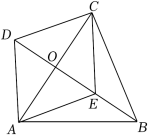（2）若AB＝BC，CD＝5，AC＝8，求四边形AECD的面积．

21．已知一次函数y＝kx+b的图象经过点（1，2）和（﹣1，6）．

（1）求这个一次函数的表达式；

（2）若这个一次函数的图象与x轴交于点A，与y轴交于点B，求S△OAB的值．

22．已知a，b都是实数，现定义新运算：a*b＝3a﹣b2，例：2*1＝3×2﹣12＝5．

（1）求2*（）的值；

（2）若m＝（）（），n＝3，求m*n的值．

23．某水果店购进甲、乙两种苹果的进价分别为8元/kg、12元/kg，这两种苹果的销售额y（元）与销售量x（kg）之间的关系如图所示．

（1）求出甲种苹果销售额y甲与销售量x之间的函数关系式；

（2）求点B的坐标，并写出点B表示的实际意义；

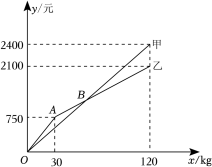（3）若不计损耗等因素，当甲、乙两种苹果的销售量均为akg（a＞30）时，它们的利润和为1695元，求a的值．

24．在平面直角坐标系xOy中，点A（a，0），B（0，b），C（m，n），点C在直线AB上，且a＞0，m＜0，|n﹣2b+1|＝0．

（1）求n和b的值；

（2）若三角形AOC的面积为6，求m的值；

（3）过点A作直线l⊥x轴，D是直线l上的一动点，若m+a，求CD的最小值．

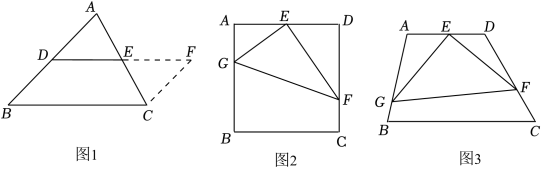
25．【方法回顾】连接三角形任意两边中点的线段叫三角形的中位线，探索三角形中位线的性质，方法如下：如图1，D、E分别是AB、AC中点，延长DE到F，使EF＝DE，连接CF；

（1）证明△ADE≌△CFE，再证四边形DBCF是平行四边形，从而得到线段DE与BC的位置关系和数量关系分别为 　        　、　                  　．

（2）【初步运用】如图2，正方形ABCD中，E为边AD中点，G、F分别在边AB、CD上，且AG＝2，DF＝3，∠GEF＝90°，求GF长．

（3）【拓展延伸】如图3，四边形ABCD中，∠A＝100°，∠D＝110°，E为AD中点，G、F分别为AB、CD边上的点，若AG＝2，DF，∠GEF＝90°，求GF长．