2022-2023学年宁夏固原市西吉县八年级（下）期末数学试卷（含解析）

这是一份2022-2023学年宁夏固原市西吉县八年级（下）期末数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年宁夏固原市西吉县八年级（下）期末数学试卷
一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列二次根式中能与2 3合并的是(    )
A. 13 B. 8 C. 18 D. 9
2. 若函数y=2 2−x有意义，则自变量x的取值范围在数轴上表示正确的是(    )
A. B.
C. D.
3. 明明在玩摆木棒游戏，帮他看一看那一组长度的木棒可以构成直角三角形(    )
A. 2，3，4 B. 3，4，6 C. 6，7，11 D. 5，12，13
4. 西吉县2023年奔跑吧少年暨第四届“体教融合杯”田径运动会期间连续四天的气温是15，20，9，x(单位：℃)这四天平均气温是15℃，则x的值为(    )
A. 12 B. 13 C. 16 D. 15
5. 在下列条件中，能判定四边形为矩形的是(    )
A. 两组对边分别平行 B. 四个内角度数相等 C. 对角线长度相等 D. 对角线互相垂直
6. 如图，《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺，问折高者几何？意思是：一根竹子，原高一丈(一丈=十尺)，一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部6尺远，则折断处离地面的高度为(    )
A. 3尺 B. 3.2尺 C. 3.6尺 D. 4尺
7. 如图，在平行四边形ABCD中，若∠A+∠C=140°，则∠D的度数为(    )

A. 100° B. 140° C. 120° D. 110°
8. 一次函数y1=mx+n与y2=mnx(m、n为常数，且mn≠0)在同一平面直角坐标内的图象可能是(    )
A. B.
C. D.
二、填空题（本大题共8小题，共24.0分）
9. 数学综合与实践活动课上，某兴趣小组要测定被池塘隔开的A、B两点间的距离，他们在AB外选一点C，连接AC、BC，并分别找出它们的中点D、E，连接DE.现测得AC=28m，BC=30m，DE=31m，则A、B两点间的距离为______ m.
10. 请写出一个图象经过二、三、四象限的一次函数解析式：______ .(答案不唯一，只要符合题意均可得分)
11. 分解因式2a2b−8b3= ______ ．
12. 命题“两直线平行，同位角相等．”的逆命题是______．
13. 双减政策落地，我县学校纷纷行动大力提升学生核心素养，学生的综合评价分学习、体育和艺术三部分，学习成绩、体育成绩与艺术成绩按5：3：2计入综合评价，若王鹏学习成绩为90分，体育成绩为80分，艺术成绩为75分，则他的综合评价得分为______ ．
14. 实数a在数轴上的位置如图所示，则 (a−3)2+ (a−10)2化简后为______．


15. 如图，在△ABC中，点D，E，F分别是BC，AC，AB的中点．若AB=6，BC=8，则四边形BDEF的周长是______．


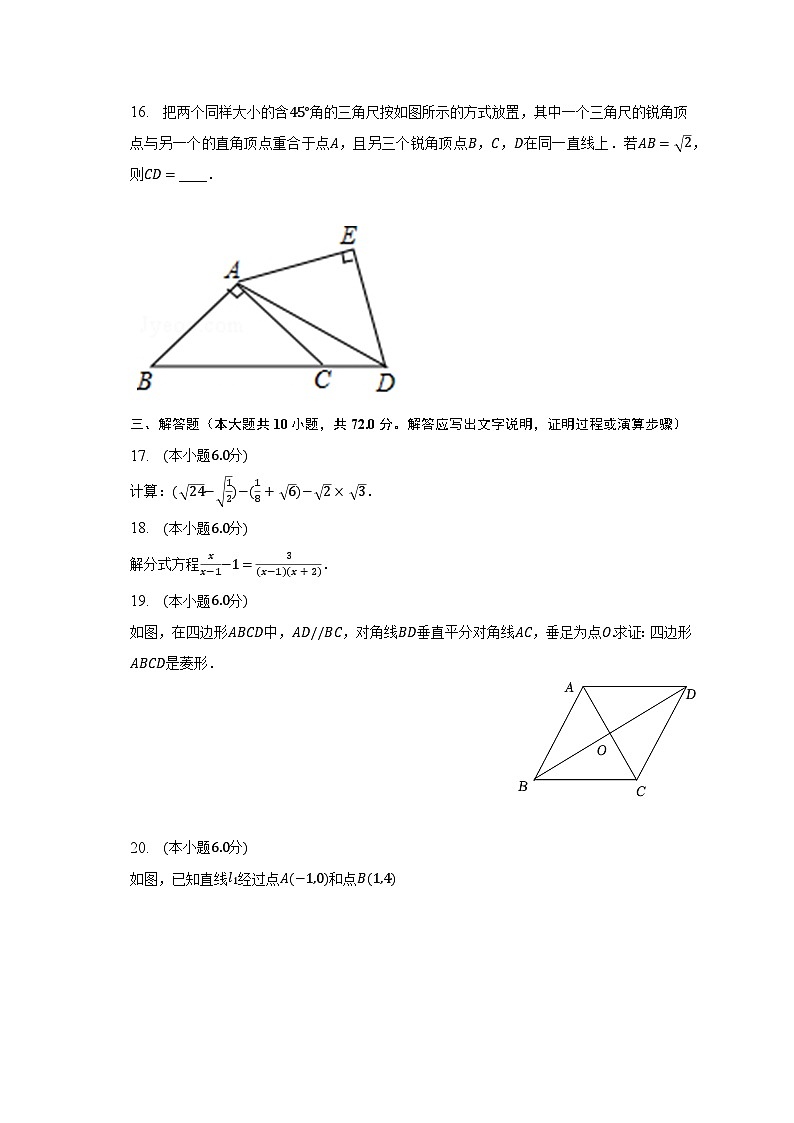
16. 把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB= 2，则CD=____．


三、解答题（本大题共10小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题6.0分)
计算：( 24− 12)−(18+ 6)− 2× 3．
18. (本小题6.0分)
解分式方程xx−1−1=3(x−1)(x+2)．
19. (本小题6.0分)
如图，在四边形ABCD中，AD//BC，对角线BD垂直平分对角线AC，垂足为点O.求证：四边形ABCD是菱形．

20. (本小题6.0分)
如图，已知直线l1经过点A(−1,0)和点B(1,4)

(1)求直线l1的解析式；
(2)若点P是x轴上的点，且△APB的面积为8，求出点P的坐标．
21. (本小题6.0分)
如图，有一只摆钟，摆锤看作一个点，当摆锤静止时，它离底座的垂直高度DE=4cm，当摆锤摆动到最高位置时，它离底座的垂直高度BF=6cm，此时摆锤与静止位置时的水平距离BC=8cm时，求钟摆AD的长度．

22. (本小题6.0分)
如图，在Rt△ABC中，∠C=90°．
(1)作∠BAC的平分线AD交边BC于点D.(尺规作图，保留作图痕迹，不写作法)．
(2)在(1)的条件下，若∠BAC=28°，求∠ADB的度数．

23. (本小题8.0分)
西吉县城乡居民在党和政府的关怀支持下都用上了自来水，但有些居民却不知道节约用水，浪费现象比较突出.为进一步提高全民“节约用水”意识，某中学组织学生进行家庭月用水量情况调查，小明和他的同伴随机抽查了几个小区和若干村组的家庭的月用水量，并根据调查结果绘制了下面两幅不完整的统计图.请根据统计图中信息，解答下列问题：

(1)请补全条形统计图；
(2)求本次调查中的所有家庭的月平均用水量；并估计某居住片区500户家庭中月用水量低于月平均用水量的家庭户数．
24. (本小题8.0分)
如图，点B，E，C，F在一条直线上，AB=DE，AB//DE，BE=CF．
(1)求证：△ABC≌△DEF；
(2)连接AD，求证：四边形ACFD是平行四边形．

25. (本小题10.0分)
西吉县龙王坝休闲乐园、西吉县下堡亲子园两家草莓采摘园的草莓品质相同，销售价格也相同.今年“五一”假期为了吸引游客，两家均推出了优惠方案，龙王坝采摘园的优惠方案：游客进园需购买50元的门票，采摘的草莓六折优惠；下堡亲子园采摘园的优惠方案：游客进园不需购买门票，采摘的草莓超过一定数量后，超过部分打折优惠.优惠期间，设某游客的草莓采摘量为x(千克)，在龙王坝采摘所需总费用为y龙王(元)，在下堡亲子园采摘园所需总费用为y下堡(元)，图中折线O−A−B表示y龙王与x之间的函数关系．
(1)求y龙王与x之间的函数关系式、y下堡与x(只求x>10时直线AB)的函数关系式；
(2)当游客采摘15千克的草莓时，你认为他在哪家草莓园采摘更划算？

26. (本小题10.0分)
如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为(−3,4)，点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H，连接BM

(1)菱形ABCO的边长______
(2)求直线AC的解析式；
(3)动点P从点A出发，沿折线ABC方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S(S≠0)，点P的运动时间为t秒，
①当0 ②在点P运动过程中，当S=3，请直接写出t的值．
答案和解析

1.【答案】A 
【解析】解：A、 13= 33；
B、 8=2 2；
C、 18=3 2；
D、 9=3；
∴与2 3合并的是 13，
故选：A．
根据同类二次根式概念解答即可．
本题考查同类二次根式，掌握同类二次根式概念是解题关键．

2.【答案】B 
【解析】解：由于函数y=2 2−x有意义，
所以2−x>0，
即x<2，
因此用数轴表示不等式的解集为：

故选：B．
根据分式、二次根式有意义的条件确定x的取值范围，再利用数轴表示不等式的解集即可．
本题考查分式、二次根式有意义的条件以及在数轴上表示不等式的解集，确定自变量x的取值范围，掌握在数轴上表示不等式解集的方法是正确解答的前提．

3.【答案】D 
【解析】解：A、∵32+22=13，42=16，
∴32+22≠42，
∴不能组成直角三角形，
故A不符合题意；
B、∵32+42=25，62=36，
∴32+42≠62，
∴不能组成直角三角形，
故B不符合题意；
C、∵62+72=85，112=121，
∴62+72≠112，
∴不能组成直角三角形，
故C不符合题意；
D、∵52+122=169，132=169，
∴52+122=132，
∴能组成直角三角形，
故D符合题意；
故选：D．
根据勾股定理的逆定理进行计算，逐一判断即可解答．
本题考查了勾股定理的逆定理，熟练掌握勾股定理的逆定理是解题的关键．

4.【答案】C 
【解析】解：由题意知，得：15+20+9+x4=15，
解得x=16，
故选：C．
根据算术平均数的定义列出关于x的方程，解之即可得出答案．
本题主要考查算术平均数，解题的关键是掌握算术平均数的定义．

5.【答案】B 
【解析】解：A、两组对边分别平行的四边形是平行四边形，故选项A不符合题意；
B、四个内角度数相等的四边形是矩形，故选项B符合题意；
C、对角线长度相等的四边形不一定是平行四边形，故选项C不符合题意；
D、对角线互相垂直的四边形不一定是平行四边形，故选项D不符合题意；
故选：B．
由矩形的判定、平行四边形的判定与性质分别对各个选项进行判断即可．
本题考查了矩形的判定、平行四边形的判定与性质等知识，熟练掌握矩形的判定和平行四边形的判定与性质是解题的关键．

6.【答案】B 
【解析】解：设竹子折断处离地面x尺，则斜边长为(10−x)尺，
根据勾股定理得：x2+62=(10−x)2，
解得：x=3.2，
∴折断处离地面的高度为3.2尺，
故选：B．
竹子折断后刚好构成直角三角形，设竹子折断处离地面x尺，则斜边长为(10−x)尺，利用勾股定理解题即可．
此题考查了勾股定理的应用，解题的关键是利用题目信息构造直角三角形，从而运用勾股定理解题．

7.【答案】D 
【解析】解：∵四边形ABCD是平行四边形，
∴∠A=∠C，∠A+∠D=180°，
∵∠A+∠C=140°，
∴∠A=70°，
∴∠D=110°，
故选：D．
根据平行四边形的对角相等，邻角互补可得答案．
本题主要考查了平行四边形的性质，熟练掌握平行四边形的性质是解题的关键．

8.【答案】A 
【解析】解：A、由一次函数的图象可知，m<0，n>0，故mn<0；由正比例函数的图象可知mn<0，两结论一致，故本选项符合题意；
B、由一次函数的图象可知，m<0，n>0，故mn<0；由正比例函数的图象可知mn>0，两结论不一致，故本选项不符合题意；
C、由一次函数的图象可知，m>0，n>0，故mn>0；由正比例函数的图象可知mn<0，两结论不一致，故本选项不符合题意；
D、由一次函数的图象可知，m>0，n<0，故mn<0；由正比例函数的图象可知mn>0，两结论不一致，故本选项不符合题意．
故选：A．
根据一次函数与正比例函数的性质对四个选项进行逐一分析即可．
此题主要考查了一次函数的图象性质，要掌握它的性质才能灵活解题．
一次函数y=kx+b的图象有四种情况：
①当k>0，b>0时，函数y=kx+b的图象经过第一、二、三象限；
②当k>0，b<0时，函数y=kx+b的图象经过第一、三、四象限；
③当k<0，b>0时，函数y=kx+b的图象经过第一、二、四象限；
④当k<0，b<0时，函数y=kx+b的图象经过第二、三、四象限．

9.【答案】62 
【解析】解：∵D、E分别是AC、BC的中点，
∴DE是△ABC的中位线，
∴AB=2DE，
∵DE=31m，
∴AB=62m，
故答案为：62．
根据三角形中位线定理解答即可．
本题考查的是三角形中位线定理，掌握三角形中位线等于第三边的一半是解题的关键．

10.【答案】y=−x−1 
【解析】解：由题意，对于一次函数y=kx+b，
∵一次函数图象过二、三、四象限，
∴k<0，b<0．
∴k=−1，b=−1.(答案不唯一．)
∴一次函数解析式为：y=−x−1．
故答案为：y=−x−1．
依据题意，由一次函数的图象与性质，对于形如y=kx+b的一次函数，若过二、三、四象限，则可得k<0，b<0，从而举例可以得解．
本题主要考查了一次函数的性质，解题时要熟练掌握并理解．

11.【答案】2b(a+2b)(a−2b) 
【解析】解：原式=2b(a2−4b2)
=2b(a+2b)(a−2b)，
故答案为：2b(a+2b)(a−2b)．
提公因式后利用平方差公式因式分解即可．
本题考查因式分解，熟练掌握因式分解的方法是解题的关键．

12.【答案】同位角相等，两直线平行 
【解析】解：∵原命题的条件为：两直线平行，结论为：同位角相等．
∴其逆命题为：同位角相等，两直线平行．
将原命题的条件与结论互换即得到其逆命题．
本题考查了互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．

13.【答案】86.5分 
【解析】解：根据题意，他的综合评价得分为90×5+80×3+75×210=86.5(分)，
故答案为：86.5分．
根据加权平均数的定义列式计算即可．
本题主要考查加权平均数，解题的关键是掌握加权平均数的定义．

14.【答案】7 
【解析】解：由数轴可得，
4 ∴ (a−3)2+ (a−10)2
=a−3+10−a
=7，
故答案为：7．
根据数轴可以求得a的取值范围，从而可以化简题目中的式子，从而可以解答本题．
本题主要考查了二次根式的性质、实数与数轴，解答本题的关键是明确二次根式的性质．

15.【答案】14 
【解析】解：∵D，E，F分别是BC，AC，AB的中点，
∴DE=BF=12AB=12×6=3，
∵E、F分别为AC、AB中点，
∴EF=BD=12BC=12×8=4，
∴四边形BDEF的周长为：2×(3+4)=14，
故答案为：14．
根据三角形中位线定理解答即可．
本题考查了三角形的中位线定理，熟练掌握三角形中位线定理是解题的关键．

16.【答案】 3−1 
【解析】
【分析】
此题主要考查了勾股定理，等腰直角三角形的性质，正确作出辅助线是解本题的关键．
先利用等腰直角三角形的性质求出BC=2，BF=AF=1，再利用勾股定理求出DF，即可得出结论．
【解答】
解：如图，过点A作AF⊥BC于F，

在Rt△ABC中，∠B=45°，
∴BC= 2AB=2，BF=AF= 22AB=1，
∵两个同样大小的含45°角的三角尺，
∴AD=BC=2，
在Rt△ADF中，根据勾股定理得，DF= AD2−AF2= 3
∴CD=BF+DF−BC=1+ 3−2= 3−1，
故答案为 3−1．  
17.【答案】解：( 24− 12)−(18+ 6)− 2× 3
=2 6− 22−18− 6− 6
=− 22−18． 
【解析】先计算二次根式的乘法，再算加减，即可解答．
本题考查了二次根式的混合运算，准确熟练地进行计算是解题的关键．

18.【答案】解：原方程两边同乘(x−1)(x+2)，去分母得：x(x+2)−(x−1)(x+2)=3，
整理得：x2+2x−x2−2x+x+2=3，
移项，合并同类项得：x=1，
检验：将x=1代入(x−1)(x+2)得：0×3=0，
则x=1是分式方程的增根，
故原分式方程无解． 
【解析】根据解分式方程的步骤解方程后进行检验即可．
本题考查解分式方程，熟练掌握解分式方程的方法是解题的关键，特别注意解分式方程时必须进行检验．

19.【答案】证明：∵AD//BC，
∴∠ADO=∠CBO，
∵对角线BD垂直平分对角线AC，
∴OA=OC，
在△ADO与△BCO中，
∠ADO=∠CBO∠DOA=∠BOCOA=OC，
∴△ADO≌△BCO(AAS)，
∴AD=BC，
又∵AD//BC，
∴四边形ABCD是平行四边形，
∵BD⊥AC，
∴平行四边形ABCD是菱形． 
【解析】由AAS证明△ADO≌△BCO，再由平行四边形的判定和菱形的判定即可得出结论．
本题考查了菱形的判定、全等三角形的判定与性质、平行四边形的判定等知识，熟练掌握菱形的判定，证明三角形全等是解题的关键．

20.【答案】解：(1)设直线l1的解析式为y=kx+b(k≠0)，
∵一次函数的图象经过点A(−1,0)和点B(1,4)．
∴−k+b=0k+b=4，
解得k=2b=2，
∴直线l1的解析式为y=2x+2；

(2)∵△APB的面积为8，点B(1,4)，
∴12×AP×4=8，
解得：AP=4，
∵点A(−1,0)，
∴P(−5,0)或(3,0)． 
【解析】(1)首先设直线l1的解析式为y=kx+b(k≠0)，根据待定系数法把点A(−1,0)和点B(1,4)代入设的解析式，即可求出一次函数的解析式；
(2)根据三角形的面积计算出AP的长，进而得到P点坐标．
此题主要考查了待定系数法求一次函数解析式，关键是掌握直线上任意一点的坐标都满足函数关系式y=kx+b．

21.【答案】解：设AB=AD=x cm，由题意得，CE=BF=6cm，
∴AC=AD+DE−CE=(x−2)cm，
∵AC2+BC2=AB2，
∴(x−2)2+82=x2，
∴x=17，
∴AD=17cm．
答：钟摆AD的长度． 
【解析】设AB=AD=x cm，表示出AC的长，然后利用勾股定理列方程求解即可．
此题考查了勾股定理的应用，在应用勾股定理解决实际问题时，勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．

22.【答案】解：(1)如图，AD为所作；

(2)∵AD平分∠BAC，
∴∠CAD=∠BAD=12∠BAC=14°，
∴∠ADB=∠CAD+∠C=14°+90°=104°． 
【解析】(1)利用基本作图作AD平分∠BAC即可；
(2)根据角平分线的定义得到∠CAD=12∠BAC=14°，然后利用三角形外角性质求∠ADB的度数．
本题考查了作图−基本作图：熟练掌握基本作图(作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线)．

23.【答案】解：(1)本次抽查的户数为：(3+1)÷20%=20，
用水量为7吨的用户有：20−2−4−6−3−1=4(户)，
补全的条形统计图如图所示；
(2)平均用水量为：4×2+5×4+6×6+7×4+8×3+9×120=6.25(吨)，
500×2+4+620
=300(户)，
答：估计小区500户家庭中月用水量低于月平均用水量的家庭有300户． 
【解析】(1)根据用水量8吨和9吨的户数和他们所占的百分比，可以计算出本次抽取的户数，然后即可计算出用水量7吨的户数，再将条形统计图补充完整即可；
(2)根据条形统计图中的数据，可以计算出小丽所住小区400户家庭中月用水量低于月平均用水量的家庭户数．
本题考查条形统计图、扇形统计图、用样本估计总体、加权平均数，解答本题的关键是明确题意，利用数形结合的思想解答．

24.【答案】证明：(1)∵AB//DE，
∴∠B=∠DEF，
∵BE=CF，
∴BE+CE=CF+CE，
即BC=EF，
在△ABC和△DEF中，
AB=DE∠B=∠DEFBC=EF，
∴△ABC≌△DEF(SAS)；
(2)由(1)得：△ABC≌△DEF，
∴AC=DF，∠ACB=∠F，
∴AC//DF，
∴四边形ACFD是平行四边形． 
【解析】(1)由SAS证明△ABC≌△DEF即可；
(2)由全等三角形的性质得AC=DF，∠ACB=∠F，则AC//DF，即可得出结论．
本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的性质等知识，熟练掌握平行四边形的判定，证明△ABC≌△DEF是解题的关键．

25.【答案】解：(1)根据题意得，龙王坝、下堡两采摘园优惠前的草莓销售价格：300÷10=30(元/千克)．
∴y龙王=30×0.6x+60=18x+60；
当x≥10时，设y下堡=kx+b，
由题意的：10k+b=30025k+b=480，
解得k=12b=180，
∴y下堡=12x+180，
∴y下堡与x之间的函数关系式为：y下堡=12x+180(x≥10)；
(2)当x=15时，y龙王=18×15+60=330，y下堡=12×15+180=360，
∴y龙王 答：他在龙王坝家草莓园采摘更划算． 
【解析】(1)根据题意得出草莓销售价格，进而求得龙王坝的函数关系式；根据函数图象待定系数法求得下堡的解析式；
(2)将x=15千克代入(1)中解析式，即可求解．
本题考查了一次函数的应用，根据题意求得函数关系式是解题的关键．

26.【答案】(1)5;
(2)∵四边形ABCO是菱形，
∴OC=OA=AB=5，即C(5,0)．
设直线AC的解析式y=kx+b，函数图象过点A、C，得
5k+b=0−3k+b=4，解得k=−12b=52，
直线AC的解析式y=−12x+52；

(3)设M到直线BC的距离为h，
当x=0时，y=52，即M(0,52)，HM=HO−OM=4−52=32，
由S△ABC=S△AMB+SBMC=12AB⋅OH=12AB⋅HM+12BC⋅h，
12×5×4=12×5×32+12×5h，解得h=52，
①当0 S=12BP⋅HM=12×32(5−2t)=−32t+154；
②当2.5 S=12BP⋅h=12×52(2t−5)=52t−254，
把S=3代入①中的函数解析式得，3=−32t+154，
解得：t=12，
把S=3代入②的解析式得，3=52t−254，
解得：t=3710．
∴t=12或3710． 
【解析】解：(1)Rt△AOH中，
AO= AH2+OH2= 42+32=5，
所以菱形边长为5；
故答案为：5；

(2)见答案；

(3)见答案．
(1)Rt△AOH中利用勾股定理即可求得菱形的边长；
(2)根据(1)即可求的OC的长，则C的坐标即可求得，利用待定系数法即可求得直线AC的解析式；
(3)根据S△ABC=S△AMB+SBMC求得M到直线BC的距离为h，然后分成P在AB上和在BC上两种情况讨论，利用三角形的面积公式求解．
本题考查了待定系数法求一次函数的解析式以及菱形的性质，根据三角形的面积关系求得M到直线BC的距离h是关键．