第一章一元二次方程复习课件PPT

这是一份第一章一元二次方程复习课件PPT，共32页。

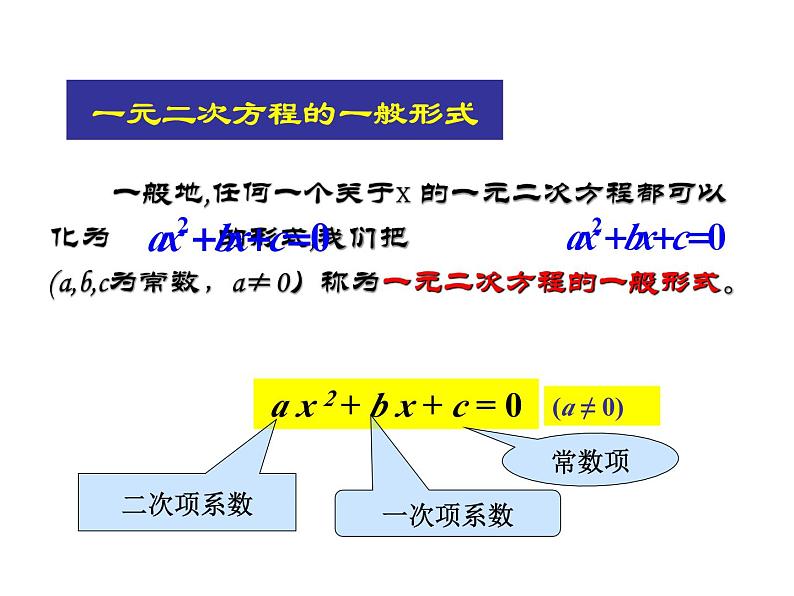
一元二次方程复习（一）一元二次方程定义解法应用 等号两边都是整式, 只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的方程叫做一元二次方程一元二次方程的概念 特点:①都是整式方程;②只含一个未知数;③未知数的最高次数是2. a x 2 + b x + c = 0(a ≠ 0)二次项系数一次项系数常数项一元二次方程的一般形式 一般地,任何一个关于x 的一元二次方程都可以化为 的形式,我们把(a,b,c为常数，a≠0）称为一元二次方程的一般形式。1、判断下面哪些方程是一元二次方程√ √ × × × × 练习二解： 原方程转化为(2a-4) x2 -2bx+a=0 当a≠2时是一元二次方程； 当a＝2,b≠0时是一元一次方程；(a,b,c为常数，a≠0）一元二次方程的一般形式2、把方程（1-x)(2-x)=3-x2 化为一般形式是：___________, 其二次项系数是____,一次项系数是____,常数项是____.3、方程（m-2)x|m| +3mx-4=0是关于x的一元二次方程，则 （ ）A.m=±2 B.m=2 C.m=-2 D.m≠ ±2 2x2-3x-1=02-3-1C你学过一元二次方程的哪些解法?说一说因式分解法开平方法配方法公式法一元二次方程的基本解法你能说出每一种解法的特点吗?（开平方法）例：用直接开平方法：(x+2)2=９一元二次方程的解法：解： (x+2)2=９ x+2=3， x+2=-3 X1=1， X2=-5 方程的左边是完全平方式,右边是非负数;即形如x2=a(a≥0)开平方法例：（2）一元二次方程的解法：解： 注：当一元二次方程二次项系数为1时用配方法比较简便。（配方法）——用配方法解一元二次方程的步骤:1.变形:把二次项系数化为12.移项:把常数项移到方程的右边;3.配方:方程两边都加上一次项系数 一半的平方;4.变形:方程左边分解因式,右边合并同类;5.开方:根据平方根意义,方程两边开平方;6.求解:解一元一次方程;7.定解:写出原方程的解.配方法例：（3）一元二次方程的解法：解：（公式法） 注：当一元二次方程二次项系数不为1且难以用因式分解时常用公式法比较简便。用公式法解一元二次方程的前提是:公式法1.必需是一般形式的一元二次方程: ax2+bx+c=0(a≠0). 2.b2-4ac≥0.（因式分解法） 解:原方程化为 （y+2) 2﹣3（y+2）=0 (y+2)(y+2-3)=0 (y+2)(y-1)=0 y+2=0 或 y-1=0 ∴y1=-2 y2=1把y+2看作一个整体，变成a×b=0形式(即两个因式的积的形式)。例：一元二次方程的解法：注：在解一元二次方程时, 要先观察方程,选择适当的方法.配方法、公式法适用于任何一个一元二次方程,但公式法首先要将方程转化为一般式,而因式分解法只适用于某些一元二次方程.总之它 的基本思路就是将二次方程转化为一次方程,即降次.1.用因式分解法的条件是:方程左边能够 分解,而右边等于零;因式分解法2.理论依据是:如果两个因式的积等于零 那么至少有一个因式等于零.因式分解法解一元二次方程的一般步骤:一移-----方程的右边=0;二分-----方程的左边因式分解;三化-----方程化为两个一元一次方程;四解-----写出方程两个解;选用适当方法解下列一元二次方程1、 (2x+1)2=64 ( 法）2、 (x-2)2-４(x+１)2=0 ( 法）3、(５x-４)2 -(4-５x)=０ ( 法）4、 x２-４x-10=０ ( 法）5、 ３x２-４x-５=０ ( 法）6、 x２＋６x-1=0 ( 法）7、 ３x２ -８x-３=０ ( 法）8、 y2- y-1=0 ( 法）选择方法的顺序是： 直接开平方法 →分解因式法 →公式法→配方法因式分解因式分解 公式公式公式因式分解公式直接开平方练习一元二次方程的根与系数：根的判别式：b2-4ac练习：1、方程2x2+3x－k=0根的判别式是 ；当k 时，方程有实根。2、方程x2+2x+m=0有两个相等实数根，则m= 。3、关于x的方程x2-(2k-1)x+(k-3)=0.试说明无论k为任何实数,总有两个不相等的实数根.4、关于x的一元二次方程mx2+(2m－1)x－2=0的根的判别式的值等于4，则m= 。 一元二次方程的根与系数的关系：若 ax2+bx+c=0 的两根为 x1、x2，则x1+x2=_______；x1x2=___；以x1、x2为根（二次项系数为1）的一元二次方程为_________________.x2-(x1+x2)x+x1x2=0一元二次方程的根与系数：韦达定理：已知两数的和是4,积是1，则此两数为 .拓展练习：１、已知方程x2－mx+2=0的两根互为相反数，则m= 。2、 已知方程x2+4x－2m=0的一个根α比另一个根β小4，则α= ；β= ；m= .3、已知方程5x2+mx－10=0的一根是－5，求方程的另一根及m的值。 4、关于x的方程2x2－3x+m=0，当 时，方程有两个正数根；当m 时，方程有一个正根，一个负根；当m 时，方程有一个根为0。 三、二次三项式的因式分解中的因式 千万不能忽略。2.在分解二次三项式的因式时，可先用求根公式求出方程的两个根x1,x2然后,写成a例题讲解例1 把分解因式此步的目的是去掉括号内的分母5、一张长方形铁皮，四个角各剪去一个边长为4cm的小正方形，再折起来做成一个无盖的小 盒子。已知铁皮的长是宽的2倍，做成的小盒子的容积是1536cm3，求长方形铁皮的长与宽 。6、一块长方形木板长40cm，宽30cm。在木板中间挖去一个底边长为20cm，高为15cm的 等宽U形孔，已知剩下的木板面积是原来面积的 ，求挖去的U形孔的宽度。 7、已知关于x的方程(m-3)x2+2x+m2-9=0有一个根是0，试确定m的值解：∵0是方程的解∴代入得m2-9=0∴ m=±3经检验 m=±3都符合题意∴ m=±38、关于x的方程(a2-4)x2+(a+2)x-1=0(1)当a取什么值时,它是一元一次方程?(2)当a取什么值时,它是一元二次方程?∴a=2∴当a=2时，原方程是一元一次方程(2) a2-4≠0∴a≠±2∴当a≠±2时，原方程是一元二次方程返回效果检测6.把方程x2+3mx=8的左边配成一个完全平方式,在方程的两边需同时加上的式子是A. 9m2 B. 9m2x2 C. D. 7.已知(1-m2-n2)(m2+n2)=-6,则m2+n2的值是A.3 B.3或-2 C.2或-3 D. 2返回8.下面是张潇同学在测验中解答的填空题，其中答对的是A．若x2=4，则x=2B．方程x(2x-1)=2x-1的解为x=1C．方程x2+2x+2=0实数根的个数为0个D．方程x2-2x-1=0有两个相等的实数根 9.已知两数的和是4,积是1，则此两数为 .效果检测返回