

2023年江苏省苏州市工业园区景城学校中考数学二模试卷(含解析)
展开2023年江苏省苏州市工业园区景城学校中考数学二模试卷
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列实数中,是无理数的是( )
A. 3.1415926 B. 1−π C. 1.010010001 D. cos60°
2. 刚刚发布的2023年全国主要城市第一季度GDP排行榜中,苏州市以5186.6亿元排名全国第七位,其中5186.6亿用科学记数法可表示为( )
A. 5.1866×1012 B. 0.51866×1012 C. 5.1866×1011 D. 51.866×1010
3. 下列运算正确的是( )
A. (a3)4=a12 B. (−2a)2=−4a2 C. a3⋅a3=a9 D. a6÷a2=a3
4. 如图是某校七年级学生参加课外兴趣小组的扇形统计图(每人只参加一项),若参加书法兴趣小组的人数是30人,则参加绘画兴趣小组的人数是( )
A. 36人
B. 40人
C. 60人
D. 200人
5. 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
A. 60° B. 50° C. 40° D. 30°
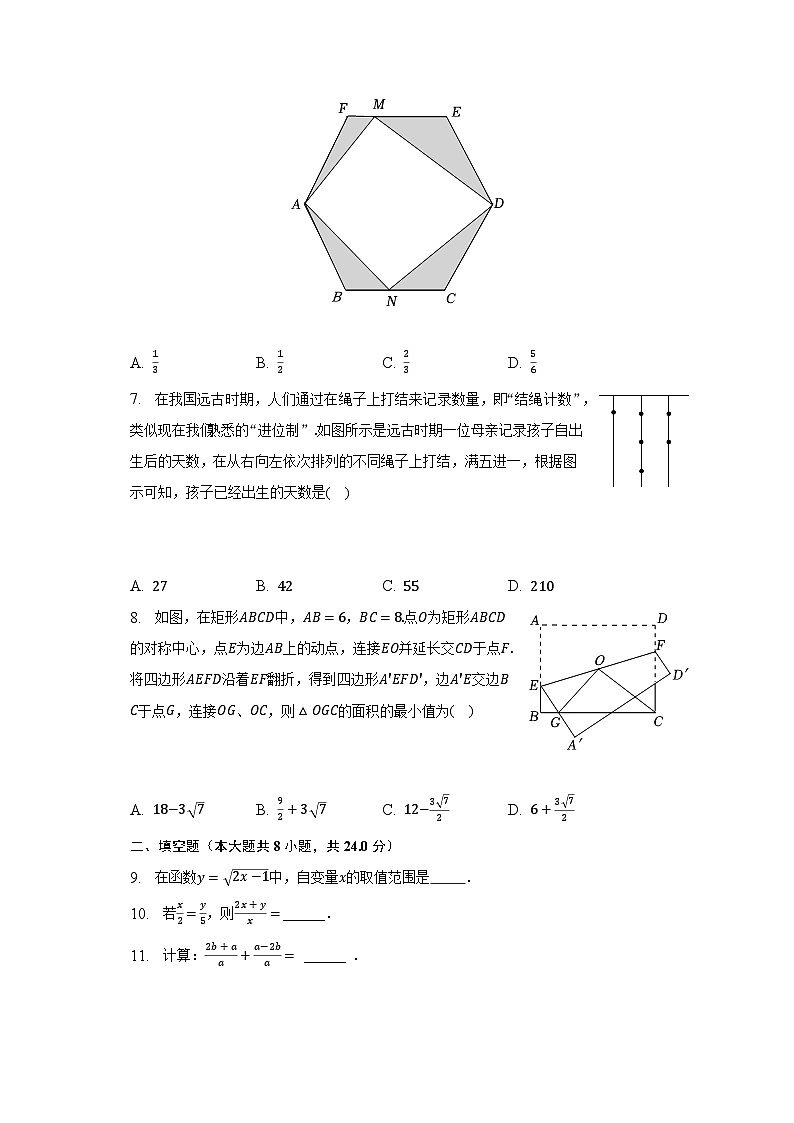
6. 如图是面积为6的正六边形ABCDEF飞镖游戏板,点M,N分别为边EF,BC上的一点,若向该六边形飞镖游戏板投掷一枚飞镖,假设飞镖击中正六边形内的每一个位置是等可能的(击中图中阴影部分的边界或没有击中正六边形板,则重投一次),任意投掷飞镖一次,飞镖击中图中阴影部分的概率是( )
A. 13 B. 12 C. 23 D. 56
7. 在我国远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,类似现在我们熟悉的“进位制”.如图所示是远古时期一位母亲记录孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满五进一,根据图示可知,孩子已经出生的天数是( )
A. 27 B. 42 C. 55 D. 210
8. 如图,在矩形ABCD中,AB=6,BC=8.点O为矩形ABCD的对称中心,点E为边AB上的动点,连接EO并延长交CD于点F.将四边形AEFD沿着EF翻折,得到四边形A′EFD′,边A′E交边BC于点G,连接OG、OC,则△OGC的面积的最小值为( )
A. 18−3 7 B. 92+3 7 C. 12−3 72 D. 6+3 72
二、填空题(本大题共8小题,共24.0分)
9. 在函数y= 2x−1中,自变量x的取值范围是 .
10. 若x2=y5,则2x+yx=______.
11. 计算:2b+aa+a−2ba= ______ .
12. 定义:一个三角形的一个角是另一个角的2倍,这样的三角形叫做“倍角三角形”.若直角△ABC是“倍角三角形”,∠C=90°,∠A≤∠B,则∠A的度数为______ .
13. 如图,在⊙O中,弦AB,CD相交于点P,∠CAB=40°,∠ABD=30°,则∠APD的度数为______ .
14. 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于12MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,若CD=3,则AB的长是______ .
15. 一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单价:min)之间的关系如图所示.在第______分钟时该容器内的水恰好为10L.
16. 如图,在菱形ABCD中,对角线AC=8cm,BD=6cm,动点E、G分别从点A、C同时出发,均以1cm/s的速度沿AB、CD向终点B、D匀速运动;同时,动点H、F也分别从点A、C出发,均以2cm/s的速度沿AD、CB向终点D、B匀速运动,顺次连接EF、FG、GH、HE.设运动的时间为ts,若四边形EFGH是矩形,则t的值为______.
三、计算题(本大题共1小题,共5.0分)
17. 解方程:1−xx−2=12−x−2.
四、解答题(本大题共10小题,共77.0分。解答应写出文字说明,证明过程或演算步骤)
18. (本小题5.0分)
计算:|− 2|−2−1− 2tan45°.
19. (本小题6.0分)
先化简,再求值:(x2x−2+42−x)÷x2+4x+4x,从−2,0,1,2中选择适当的数代入计算.
20. (本小题6.0分)
为弘扬中华民族传统文化,某市举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小华参加“单人组”,他从中随机抽取一个比赛项目,恰好抽中“论语”的概率是______ .
(2)小明和小红组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次.则小明和小红都没有抽到“三字经”的概率是多少?请用画树状图或列表的方法进行说明.
21. (本小题6.0分)
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF//BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.
22. (本小题8.0分)
某村深入贯彻落实习近平新时代中国特色社会主义思想,认真践行“绿水青山就是金山银山”理念.在外打工的王大叔返回家乡创业,承包了甲、乙两座荒山,各栽100棵小枣树,发现成活率均为97%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两座山上随意各采摘了4棵树上的小枣,每棵的产量如折线统计图所示.
(1)直接写出甲山4棵小枣树产量的中位数______ ;
(2)分别计算甲、乙两座山小枣样本的平均数,并判断哪座山的样本的产量高;
(3)用样本平均数估计甲乙两座山小枣的产量总和.
23. (本小题8.0分)
如图,一次函数y1=ax+b与反比例函数y2=kx的图象相交于A(1,6),B(6,1)两点.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)在平面内存在点P,使得点A、点B关于点P成中心对称的点恰好落在坐标轴上,请直接写出点P的坐标为______ .
(3)连接AO、BO,点P是x轴上一点,若△ABP的面积等于△ABO面积的一半,求点P的坐标.
24. (本小题8.0分)
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A、D的⊙O分别交AB、AC于点E、F.
(1)求证:BC是⊙O的切线;
(2)若BE=8,sinB=513,求⊙O的半径;
(3)在(2)的条件下,求AD的长.
25. (本小题10.0分)
某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润
B型利润
甲店
200
170
乙店
60
150
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求由x的取值范围;
(2)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
26. (本小题10.0分)
如图,已知抛物线y=ax2+bx−8与x轴交于点A(−2,0),B(8,0)两点,与y轴交于点C,点P是直线BC下方抛物线上一动点,过点P作直线PE//y轴,交直线BC于点D,交x轴于点F,以PD为斜边,在PD的右侧作等腰直角△PDF.
(1)求抛物线的表达式,并直接写出直线BC的表达式;
(2)设点P的横坐标为m(0
27. (本小题10.0分)
【材料阅读】在等腰三角形中,我们把底边与腰长的比叫做顶角的张率(scop).如图1,在△XYZ中,XY=XZ,顶角X的张率记作scop∠X=底边腰=YZXY.容易知道一个角的大小与这个角的张率也是相互唯一确定的,所以,类比三角函数,我们可按上述方式定义∠α(0°<∠α<180°)的张率,例如,scop60°=1,scop90°= 2,请根据材料,完成以下问题:
如图2,P是线段AB上的一动点(不与点A,B重合),点C,D分别是线段AP,BP的中点,以AC,CD,DB为边分别在AB的同侧作等边三角形△ACE,△CDF,△DBG,连接PE和PG.
(1)【理解应用】
①若等边三角形△ACE,△CDF,△DBG的边长分别为a,b,c,则a,b,c三者之间的关系为______ ;
②scop∠EPG= ______ ;
(2)【猜想证明】如图3,连接EF,FG,猜想scop∠EFG的值是多少,并说明理由;
(3)【拓展延伸】如图4,连接EF,EG,若AB=12,EF=2 7,则△EPG的周长是多少?此时AP的长为多少?(可直接写出上述两个结果)
答案和解析
1.【答案】B
【解析】解:A,3.1415926,是有限小数,属于有理数.不符合题意;
B,1−π是无限不循环小数,属于无理数.符合题意;
C,1.010010001是有限小数,属于有理数.不符合题意;
D,cos60°=12是有理数,不符合题意.
故选:B.
根据无理数的定义进行判断即可.
本题考查了无理数的定义,无限不循环小数是无理数.
2.【答案】C
【解析】解:5186.6亿=518660000000=5.1866×1011.
故选:C.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于或等于10时,n是正整数;当原数的绝对值小于1时,n是负整数.
本题主要考查科学记数法,掌握形式为a×10n,其中1≤|a|<10,n为整数是解题的关键.
3.【答案】A
【解析】解:A、(a3)4=a12,故A符合题意;
B、(−2a)2=4a2,故B不符合题意;
C、a3⋅a3=a6,故C不符合题意;
D、a6÷a2=a4,故D不符合题意;
故选:A.
利用幂的乘方的法则,积的乘方的法则,同底数幂的乘法的法则,同底数幂的除法的法则对各项进行运算即可.
本题主要考查幂的乘方与积的乘方,同底数幂的乘法,同底数幂的除法,解答的关键是对相应的运算法则的掌握与应用.
4.【答案】C
【解析】解:∵参加书法兴趣小组的人数是30人,占参加课外兴趣小组人数的1−35%−30%−20%=15%,
∴参加课外兴趣小组人数的人数共有:30÷15%=200(人),
∴参加绘画兴趣小组的人数是200×30%=60(人).
故选:C.
用1减去所有已知百分比,求出参加书法兴趣小组的人数所占的百分比,根据参加书法兴趣小组的人数是30人,计算出总人数,再用参加绘画兴趣小组的人数所占的百分比乘以总人数即可得出答案.
本题考查了扇形统计图,扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.从图中找到相关信息是解此类题目的关键.
5.【答案】B
【解析】
【分析】
此题考查了平行线的性质.注意两直线平行,同位角相等定理的应用是解此题的关键.
由两直线平行,同位角相等,可求得∠3的度数,然后求得∠1的度数.
【解答】
解:如图,
∵∠2=40°,
∴∠3=∠2=40°,
∴∠1=90°−40°=50°.
故选:B.
6.【答案】A
【解析】解:如图,连接AD,CE,BF,交点为O,
由正六边形ABCDEF可得,EF=12AD,AD//EF//BC,
设EF=AO=DO=a,设EF与AD的距离为h,
∵四边形ADEF的面积=12×6=3,
∴3×12×ah=3,
∴ah=2,
∴S△ADM=12×2a×h=2,
同理可得S△ADN=2,
∴S阴影=S正六边形ABCDEF−S△ADM−S△ADN=2,
∴任意投掷飞镖一次,飞镖击中图中阴影部分的概率是26=13.
故选:A.
设EF=AO=DO=a,设EF与AD的距离为h,根据四边形ADEF的面积=12×6=3,得3×12×ah=3,所以S△ADM=12×2a×h=2,S△ADN=2,所以S阴影=S正六边形ABCDEF−S△ADM−S△ADN=2,根据概率公式即可求出答案.
本题考查了几何概率,正六边形的性质,平行线间的距离相等.解题的关键在于确定阴影部分面积为正六边形的面积与空白部分面积的差.
7.【答案】B
【解析】
【分析】
本题主要考查了进位制,解题的关键是会将五进制转化成十进制.
由题可知,孩子出生的天数的五进制数为132,化为十进制数即可.
【解答】
解:根据题意得:
孩子出生的天数的五进制数为132,
化为十进制数为:1×52+3×51+2=42.
故选:B.
8.【答案】D
【解析】解:在EA上截取EM=EG,连接OM,
由折叠得:∠MEO=∠GEO,
又∵EO=EO,
∴△MOE≌△GOE,
∴OM=OG,
∴OM最短时,OG也就最短,
而当OM⊥AB时,OM最短,
此时,∵点O为矩形ABCD的对称中心,
∴OM=12BC=4=OG,
即OG的最小值是4,
在△OGC中,∵点O为矩形ABCD的对称中心,
∴OC长度是矩形对角线长度的一半,即是5,定值,∠BCO度数也不变,是定值,
∴当OG=4最小值时,△OGC面积最小.
过点O作OH⊥BC,
∵点O为矩形ABCD的对称中心,
∴OH=12AB=3,
∴Rt△OGH中,GH= OG2−OH2= 42−32= 7,
Rt△OHC中,HC= OC2−OH2= 52−32=4,
∴GC=GH+HC= 7+4,
∴△OGC面积的最小值是12GC·OH=12×( 7+4)×3=32 7+6.
故选:D.
本题考查中心对称、轴对称、全等三角形的判定与性质以及垂线段最短等知识,解题关键是找到OG的最小值.
9.【答案】x≥12
【解析】
【分析】
本题考查函数自变量取值范围的求法以及二次根式有意义的条件.
根据被开方数大于等于0可知:2x−1≥0,解得x的范围.
【解答】
解:根据题意得:2x−1≥0,
解得,x≥12.
故答案为:x≥12.
10.【答案】92
【解析】解:设x2=y5=k,则x=2k,y=5k,
∴2x+yx=4k+5k2k=92.
故答案为:92.
设x2=y5=k,则x=2k,y=5k,代入2x+yx求解即可.
本题考查比例线段,解题的关键是掌握比例线段的性质,属于中考常考题型.
11.【答案】2
【解析】解:2b+aa+a−2ba
=2b+a+a−2ba
=2aa
=2,
故答案为:2.
根据同分母分式加法计算法则求解即可.
本题主要考查了同分母分式加法计算,掌握同分母分式加法计算法则是关键.
12.【答案】45°或30°
【解析】解:当∠C=2∠A时,
∵∠C=90°,
∴∠A=45°,
当∠B=2∠A时,
∵∠C=90°,
∴∠B+∠A=90°,
∴2∠A+∠A=90°,
∴∠A=30°,
故答案为:45°或30°.
分∠C=2∠A、∠B=2∠A两种情况,根据直角三角形的性质计算即可.
本题考查的是直角三角形的性质,掌握直角三角形两锐角互余、灵活运用分情况讨论思想是解题的关键.
13.【答案】70°
【解析】解:∵∠APD=∠B+∠D
又∵∠A=∠D=40°,∠B=30°,
∴∠APD=∠B+∠D=70°,
故答案为:70°.
利用圆周角定理以及三角形的外角的性质解决问题.
本题考查圆周角定理,三角形的外角的性质等知识,解题的关键是掌握圆周角定理,属于中考常考题型.
14.【答案】6 3
【解析】解:∵∠C=90°,∠B=30°,
∴∠BAC=60°,
由作法得AD平分∠BAC,
∴∠CAD=12∠BAC=30°,
∴AC= 3CD=3 3,
∵∠B=30°,
∴AB=2AC=6 3.
故答案为:6 3.
先利用基本作图得到AD平分∠BAC,则∠CAD=30°,然后根据含30度角的直角三角形三边的关系计算出AC=3 3,从而得到AB的长.
本题考查了作图−基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了角平分线的性质和含30度角的直角三角形三边的关系.
15.【答案】2或1713
【解析】解:由图象0−4分钟,水量每分钟增加5升,则增加到10升需2分钟.在4−12分钟,水的体积增加10升,则每分钟增加54升.
∵此时,进水和出水管同时打开
∴出水管的出水速度是每分钟5−54=154升
∴水的体积从30升降到10升用时为30−10154=163分
此时时间为第12+163=1713
故答案为:2或1713
本题是一次函数实际应用问题.解题关键是根据图象求出进水管和出水管的进出水速度,分别计算水量增加到10升和降到10升的时间即可.
16.【答案】3215
【解析】·解:∵四边形ABCD是菱形,
∴AO=CO=4cm,DO=BO=3cm,AC⊥BD,∠DAB=∠BCD,
∴BC= OB2+OC2=5cm,
∵动点E、G分别从点A、C同时出发,均以1cm/s的速度沿AB、CD向终点B、D匀速运动;同时,动点H、F也分别从点A、C出发,均以2cm/s的速度沿AD、CB向终点D、B匀速运动,
∴AE=CG=t(cm),AH=CF=2t(cm),
在△AEH和△CGF中,
AE=CG∠HAE=∠FCGAH=CF,
∴△AEH≌△CGF(SAS),
∴HE=GF,
同理可证:HG=EF,
∴四边形EFGH是平行四边形,
如图,连接EG,HF,过点O作OM⊥DC于M,ON⊥BC于N,
当EG=HF时,四边形EFGH是矩形,
即当OG=OF时,四边形EFGH是矩形,
∵S△BOC=12OB·OC=12BC·ON,
∴ON=125,
∴BN= OB2−ON2=95,
∴CN=165,
同理可求:OM=125=ON,CM=165=CN,DM=BN=95,
在Rt△ONF和Rt△OMG中,
ON=OMOF=OG,
∴Rt△ONF≌Rt△OMG(HL),
∴MG=FN,
∴165−t=2t−165,
∴t=3215,
故答案为:3215.
先证四边形EFGH是平行四边形,则当OG=OF时,四边形EFGH是矩形,由“HL”可证Rt△ONF≌Rt△OMG,可得MG=FN,即可求解.
本题考查了矩形的性质,菱形的性质,全等三角形的判定和性质,勾股定理等知识,灵活运用这些性质解决问题是解题的关键.
17.【答案】解:方程两边同乘(x−2)得:
1−x=−1−2(x−2),
解得:x=2,
检验:当x=2时,x−2=0,故此方程无解.
【解析】此题主要考查了分式方程的解法,正确掌握解题方法是解题关键.
直接找出公分母进而去分母解方程,再检验即可.
18.【答案】解:|− 2|−2−1− 2tan45°
= 2−12− 2×1
= 2−12− 2
=−12.
【解析】先计算负整数指数幂、绝对值和特殊角的三角函数值,再计算乘法,最后计算加减.
此题考查了实数的混合运算能力,关键是能准确确定运算顺序和方法,并能进行正确地计算.
19.【答案】解:(x2x−2+42−x)÷x2+4x+4x
=x2−4x−2⋅x(x+2)2
=(x+2)(x−2)x−2⋅x(x+2)2
=xx+2,
要使分式有意义,x−2≠0且x+2≠0且x≠0,
所以x不能为2,−2和0,
取x=1,
当x=1时,原式=11+2=13.
【解析】先根据分式的加减法法则进行计算,再根据分式的除法法则把除法变成乘法,算乘法,根据分式有意义的条件求出x不能为2,−2和0,取x=1,最后代入求出答案即可.
本题考查了分式的化简求值,能正确根据分式的运算法则进行计算是解此题的关键.
20.【答案】14
【解析】解:(1)他从中随机抽取一个比赛项目,恰好抽中“三字经”的概率为14,
故答案为:14;
(2)画树状图为:
共有12种等可能的结果数,其中小明和小红都没有抽到“三字经”的结果数为6;
所以小明和小红都没有抽到“三字经”的概率=612=12.
(1)直接利用概率公式求解;
(2)先画树状图展示所有12种等可能的结果数,再找出恰好小明和小红都没有抽到“三字经”的结果数,然后根据概率公式求解.
本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.
21.【答案】证明:(1)∵AF//BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
∠AFE=∠DBE∠FEA=∠BEDAE=DE,
∴△AFE≌△DBE(AAS);
(2)由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF//BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=12BC,
∴四边形ADCF是菱形.
【解析】本题考查了全等三角形的性质和判定,平行四边形的判定,菱形的判定,主要考查学生的推理能力.
(1)根据AAS证△AFE≌△DBE;
(2)利用(1)中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论.
22.【答案】38
【解析】解:(1)∵甲山4棵枣树产量为34、36、40、50,
∴甲山4棵小枣树产量的中位数为36+402=38(千克).
故答案为:38;
(2)x甲−=50+36+40+344=40(千克),
x乙−=36+40+48+364=40(千克),
∴两山的样本产量相同;
(3)(40×100+40×100)×0.97=7760(千克),
答:用样本平均数估计甲乙两座山小枣产量总和为7760千克.
(1)根据中位数的定义求解可得;
(2)根据平均数的定义分别计算出甲、乙两山样本的产量,据此可得;
(3)用平均数乘以枣树的棵树,求得两山的产量和,再乘以成活率即可得.
本题主要考查折线统计图及中位数、平均数,解题的关键是了解中位数和平均数的定义,根据折线统计图得出解题所需的数据.
23.【答案】(12,12)或(3,3)
【解析】解:(1)∵反比例函数y2=kx的图象过A(1,6),B(6,1)两点.
∴k=1×6=6×1=6,
∴反比例函数的关系式为y2=6x,
∵一次函数y1=ax+b的图象过A(1,6),B(6,1)两点.
∴k+b=66k+b=1,
解得k=−1b=7,
∴一次函数的关系式为y1=−x+7,
答:一次函数的关系式为y1=−x+7,反比例函数的关系式为y2=6x;
(2)如图1−①,点A关于点P的对称点A′在x轴上,点B关于点P的对称点B′在y轴上,
即点P是AA′的中点,也是BB′的中点,
∵OB′//PQ//BN,BP=B′P,
∴OQ=QN=12ON=3,
即点P的横坐标为3,
同理点P的纵坐标为3,
∴点P2的坐标为(3,3),
如图1−②,点A关于点P的对称点A′在y轴上,点B关于点P的对称点B′在x轴上,
即点P是AA′的中点,也是BB′的中点,
同理可求出点P的横坐标为12,纵坐标为12,
此时点P(12,12),
故答案为:(12,12)或(3,3);
(3)如图2,直线AB,即直线y=−x+7与x轴的交点C的坐标为(7,0),
根据平行线等分线段定理可得,
当OP=12OC或CP′=12OC时,△ABP的面积等于△ABO面积的一半,
∴OP=CP′=12×7=72,
∴点P(72,0)或点P′(212,0),
综上所述,点P的坐标为(72,0)或(212,0).
(1)根据待定系数法分别求出一次函数、反比例函数的关系式;
(2)由中心对称的定义以及平行线等分线段定理可得答案;
(3)利用三角形面积公式以及平行线等分线段定理得出答案即可.
本题考查一次函数、反比例函数图象的交点坐标,掌握一次函数、反比例函数图象上点的坐标特征以及平行线等分线段定理是正确解答的前提.
24.【答案】(1)证明:如图,连接OD,
则OA=OD,
∴∠ODA=∠OAD,
∵AD是∠BAC的平分线,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD//AC,
∴∠ODB=∠C=90°,
∵点D在⊙O上,
∴BC是⊙O的切线.
(2)解:∵∠BDO=90°,
∴sinB=ODBO=ODBE+OD=513,
∴OD=5,
∴⊙O的半径为5;
(3)如图2,连接EF,
∵AE是直径,
∴∠AFE=90°=∠ACB,
∴EF//BC,
∴∠AEF=∠B,
又∵∠AEF=∠ADF,
∴∠B=∠ADF,
又∵∠OAD=∠CAD,
∴△DAB∽△FAD,
∴ADAB=AFAD,
∴AD2=AB⋅AF.
∵BE=8,OE=AO=5,
∴AB=18,AE=10,
∵sinB=sin∠AEF=AFAE=513,
∴AF=5013,
∴AD2=18×5013=90013,
∴AD=30 1313.
【解析】(1)先判断出OD//AC,得出∠ODB=90°,即可得出结论;
(2)由锐角三角函数可得sinB=ODBO=ODBE+OD=513,即可求解;
(3)由锐角三角函数可求AF的长,通过证明△DAB∽△FAD,可得ADAB=AFAD,可得结论.
本题是圆的综合题,考查了圆的有关知识,锐角三角函数,相似三角形的判定和性质,熟练运用这些性质进行推理是本题的关键.
25.【答案】解:(1)分配给甲店A型产品x件,则分配给甲店B型产品(70−x)件,分配给乙店A型产品(40−x)件,分配给乙店B型产品30−(40−x)=(x−10)件,
∴W=200x+170(70−x)+60(40−x)+150(x−10)=20x+12800,
∵ x≥070−x≥040−x≥0x−10≥0,
∴10≤x≤40,
∴y=20x+12800(10≤x≤40);
(2)由题意得:W=(200−a)x+170(70−x)+60(40−x)+150(x−10),
即W=(20−a)x+12800,
∵200−a>170,
∴a<30.
当0
∴当x=40时,总利润最大,此时分配给甲店A产品40件,B产品30件,分配给乙店A产品0件,B产品30件;
当a=20时,x的取值在10≤x≤40内的所有方案利润相同;
当20
【解析】(1)求出分配给甲店A型产品x件,则分配给甲店B型产品(70−x)件,分配给乙店A型产品(40−x)件,分配给乙店B型产品30−(40−x)=(x−10)件,再根据表格表示出各利润相加即可;
(2)求出a的范围,再分三种情况根据一次函数性质讨论.
本题考查一次函数的应用,解题的关键是读懂题意,将现实生活中的问题转化为数学问题解决.
26.【答案】解:(1)把A(−2,0),B(8,0)分别代入y=ax2+bx−8中,
则4a−2b−8=064a+8b−8=0,
解得a=12b=−3,
∴抛物线的表达式为y=12x2−3x−8;
令x=0.则y=−8,
∴C(0,−8),
设直线BC解析式为y=kx−8(k≠0),
把B(8,0)代入解析式得,8k−8=0,
解得:k=1,
∴直线BC解析式为y=x−8;
(2)∵点P的横坐标为m(0
∴PD=(m−8)−(12m2−3m−8)=−12m2+4m,
过点P作PN⊥PD于N,
∵△PDF是等腰直角三角形,PD为斜边,
∴PN=DN,
∴FN=12PD,
∴SPDF=12PD⋅FN=14PD2=9,
∴PD=6,
∴−12m2+4m=6,
解得:m1=6,m2=2,
又∵0
(3)存在,理由如下:由(2)得△BOC为等腰直角三角形,
∴∠ACO+∠BCM=∠ABC=∠BCO=45°,
①如图,当点M在BC的上方时,设CM与x轴交于一点D,
∵∠ACO+∠BCD=∠ABC=∠BCO=∠OCD+∠BCD,
∴∠ACO=∠DCO,
∵OC⊥AD,OC=OC,
∴△AOC≌△COD(ASA),
∴OD=OA=2,
∴D(2,0),
设直线CM解析式为y=nx−8(n≠0),
则2n−8=0,
解得:n=4,
∴直线CM解析式为y=4x−8,
则y=4x−8y=12x2−3x−8,
解得:x=14y=48或x=0y=−8(舍去),
∴此时点M的坐标为(14,48);
②如图,当点M在BC的下方时,
过B作x轴的垂线,过C作y轴的垂线,两条垂线交于一点H,作∠HCK=∠ACO,CK交抛物线与点M,
由(2)得△BOC为等腰直角三角形,
∴∠ABC=∠BCO=45°,
∴∠BCH=45°,
即∠BCM+∠MCH−45°,
∵∠ACO+∠BCM=∠ABC=45°,
∴∠ACQ=∠MCH,
又∵∠ACO=∠HCK=90°,
∵OB=OC.∠COB=∠OCH=∠OBH=90°,
∴四边形OCHB正方形,
∵OC=OH,
∴△AOC≌△KHC(ASA),
∴KH=OA=2,
∴BK=BH−KH=8−2=6,
∴K(8,−6),
设直线CK的解析式为y=ex−8(e≠0),
∴−6=8e−8,
解得:e=14,
∴直线CK的解析式为y=14x−8,
则y=14x−8y=12x2−3x−8,
解得x=132y=−518或x=0y=−8(舍去),
∴M(132,−518);
综上所述,点M坐标为(14,48)或(132,−518).
【解析】(1)利用待定系数法求出抛物线的解析式,再求出C点坐标,然后利用待定系数法求直线BC的表达式即可;
(2)设出P(m,12m2−3m−8),D(m,m−8),然后根据两点间距离公式表示出PD长,再根据等腰三角形的性质列出△PDF的面积表达式,结合面积为9建立方程求解,即可解决问题;
(3)分点M在BC的上方和点M在BC的下方两种情况讨论,根据题意画出图形,构造三角形全等,求出直线CM上的一点坐标,则可利用待定系数法求出直线CM的解析式,最后和抛物线的解析式联立求解,即可求出点M的坐标.
本题是二次函数综合题,考查了二次函数与一次函数的交点问题,二次函数的动态几何问题,二次函数与面积的综合,全等三角形的判定和性质,相似三角形的判定和性质以及正方形的性质,解题的关键是能够综合运用所学的数学知识解决问题.
27.【答案】b=a+c 3
【解析】解:(1)①∵点C,D分别是线段AP,BP的中点,
∴AC=CP,BD=PD,
∵AC=a,BD=c,
∴CD=CP+PD=a+c,
即b=a+c,
故答案为:b=a+c;
②由题意得,EC=CP,∠ECP=120°,
∴∠EPC=12×(180°−120°)=30°,
同理,∠GPD=30°,
∴∠EPG=180°−30°−30°=120°,
∴scop∠EPG=scop120°= 3.
故答案为:b=a+c, 3;
(2)猜想:scop∠EPG= 3.
理由:如图3中,连接PF.
∵点C是AP的中点,△ACE,△CDF都是等边三角形,
∴CP=CE,∠ECF=∠PCF=60°,
∵CF=CF,
∴△ECF≌△PCF(SAS),
∴∠EFC=∠PFC,
同理可得,∠GFD=∠PFD,
∴∠EFG=2∠CFD=120°,
∴scop∠EPG=scop120°= 3;
(3)∵△ECF≌△PCF,
∴EF=PF,
同理可证:GF=PF,
∴EF=GF,
∵∠EFG=120°,EF=2 7,
∴EG= 3EF=2 21,
∵点C,D分别是线段AP,BP的中点,等边三角形△ACE,△CDF,△DBG的边长分别为a,b,c,
∴PC=AC=CE=a,PD=BD=DG=c,∠ECP=∠PDG=120°,
∴EP= 3PC= 3a,PG= 3PD= 3c,
∴EP+PG= 3(a+c)= 32AB=6 3,
∴EG+EP+PG=2 21+6 3.
如图4中,过点F作FH⊥CE交CE的延长线于点H.
∵CF=CD=b=12AB=6,∠ECF=60°,
∴FH=CF⋅sin60°=3 3,CH=CF⋅cos60°=3,
在Rt△EFH中,HE= EF2−FH2= (2 7)2−(3 3)2=1,
∴CE=CH−HE=3−1=2,
∴AP=2CE=4,
由对称性可知,AP=12−4=8,
综上所述,AP的值为4或8.
(1)①利用中点的定义,证明CD=AC+BD,可得结论;
②证明∠EPG=120°,可得结论;
(2)猜想:scop∠EPG= 3.如图3中,连接PF.证明∠EFG=2∠CFD=120°,可得结论;
(3)证明EP+PG= 3(a+c)= 32AB=6 3,可得EG+EP+PG=2 21+6 3.如图4中,过点F作FH⊥CE交CE的延长线于点H.求出AP的值,再利用对称性解决问题即可.
本题属于三角形综合题,考查了等边三角形的性质,解直角三角形,全等三角形的判定和性质等知识,解题的关键是理解题意,正确寻找全等三角形解决问题.
2023年江苏省苏州市工业园区中考数学二模试卷(含解析): 这是一份2023年江苏省苏州市工业园区中考数学二模试卷(含解析),共27页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023年江苏省苏州市工业园区星汇学校中考数学二模试卷(含解析): 这是一份2023年江苏省苏州市工业园区星汇学校中考数学二模试卷(含解析),共30页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








