北师版·河南省郑州市二七区第四初级中学八年级上学期期中测试卷（数学）

这是一份北师版·河南省郑州市二七区第四初级中学八年级上学期期中测试卷（数学），共10页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。
八年级上学期第一次线上教学反馈
一、选择题（每题3个反馈点，共30个反馈点）
1. 在实数，，0，，2.10010001，中，是无理数的有（）
A. 1个 B. 2个 C. 3个 D. 4个
2. 下列各式中正确的是（ ）
A. B. C. D.
3. 如图，笑脸盖住的点的坐标可能为（ ）

A. B. C. D.
4. 已知的三条边分别为a，b，c，下列条件不能判断是直角三角形的是（ ）
A. B. ，，
C D.
5. 下列说法：①数轴上的点与实数成一一对应关系；②一个数的算术平方根仍是它本身的数有三个；③任何实数不是有理数就是无理数；④两个无理数的和还是无理数；⑤无限小数都是无理数，正确的个数有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
6. 《九章算术》中第七章《盈不足》记载了一个问题：“今有共买物，人出八，赢三；人出七，不足四．问人数、物价各几何？”译文：“现有一些人合伙购买物品，若每人出8钱，则多出3钱；若每人出7钱，则还差4钱，问人数、物品价格各是多少？”设有x个人，物品价格为y钱，则下列方程组中正确的是（ ）
A. B. C. D.
7. 在“双减”政策下，某学校规定，学生的学期学业成绩由三部分组成：平时成绩占，期中成绩占，期末成绩占，小颖的平时、期中、期末成绩分别为85分，90分，92分，则小颖本学期的学业成绩为（ ）
A. 92分 B. 91分 C. 90分 D. 89分

8. 已知点P的坐标为，且点P到两坐标轴距离相等，则a的值为（ ）
A. 或2 B. 或1 C. 或 D. 或
9. 如图，在平面直角坐标系中，，，，，一只瓢虫从点A出发以2个单位长度/秒的速度沿循环爬行，问第2020秒瓢虫在（ ）处．

A. B. C. D.
10. 如图，、、、，点P在x轴上，直线将四边形面积分成两部分，求的长度（ ）．

A. B. C. D. 或
二、填空题（每题3个反馈点，共15个反馈点）
11. 的平方根是 ．
12. 比较大小：______．
13. 若方程组的解满足，则a的值为______．
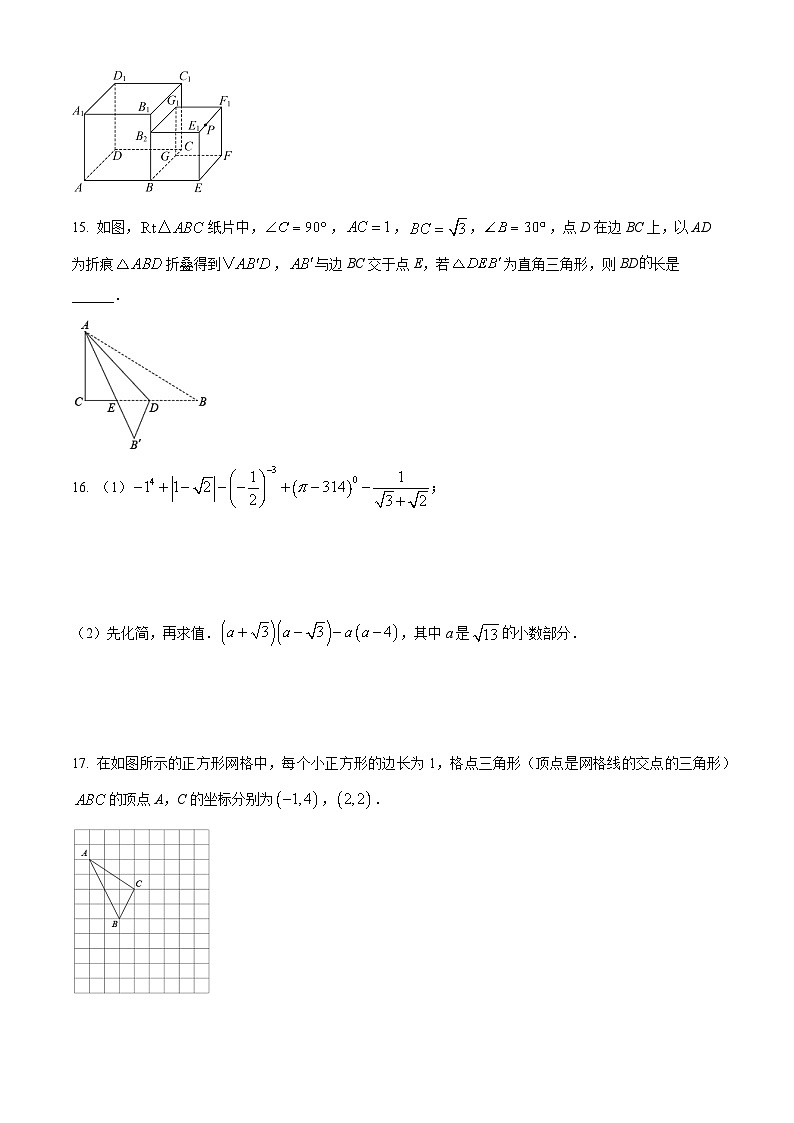
14. 棱长分别为两个正方体如图放置，点P在上，且，一只蚂蚁如果要沿着长方体的表面从点A爬到点P，需要爬行的最短距离是______．

15. 如图，纸片中，，，，，点D在边BC上，以AD为折痕折叠得到，与边BC交于点E，若为直角三角形，则BD长是______．

16. （1）；



（2）先化简，再求值．，其中a是小数部分．



17. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）的顶点A，C的坐标分别为，．

（1）请在如图所示的网格平面内作出平面直角坐标系，并作出关于y轴对称的；
（2）求面积；
（3）已知P为x轴上一点，使得的面积等于，求出点P的坐标．



18. 2022年新冠肺炎疫情席卷全国，全国人民万众一心，抗战疫情，为了早日取得抗疫的胜利，各级政府、各大新闻媒体都加大了对防疫知识的宣传，某校为了解全校共1200名同学对防疫知识的掌握情况，对他们进行了防疫知识测试，现随机抽取甲、乙两班各15名同学的测试成绩（满分100分）进行整理分析，过程如下：
【收集数据】甲班15名学生测试成绩分别为：78，83，89，97，98，85，100，94，87，90，93，92，99，95，100．
乙班15名学生测试成绩分别为：81，82，83，85，87，96，87，92，94，95，87，93，95，96，97．
【分析数据】
班级
平均数
众数
中位数
方差
甲
92
100

47.3
乙
90

91
29.7

（1）根据以上信息，可以求出：______分，______分；
（2）若规定测试成绩95分及其以上为优秀，请你根据甲乙两班的测试成绩估计参加防疫知识测试的1200名学生中成绩为优秀的学生共有多少人？
（3）根据以上数据，你认为哪个班的学生防疫测试的整体成绩较好？请说明理由．




19. 如图，在一条绷紧的绳索一端系着一艘小船．河岸上一男孩拽着绳子另一端向右走，绳端从C移动到E，同时小船从A移动到B，且绳长始终保持不变．回答下列问题：

（1）根据题意可知：AC______（填“＞”、“＜”、“＝”）．
（2）若米，米，米，求小男孩需向右移动距离．（结果保留根号）


20. 随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具，某汽车销售公司计划购进一批新能源汽车尝试进行销售，据了解2辆A型汽车、3辆B型汽车的进价共计80万元；3辆A型汽车、2辆B型汽车的进价共计95万元．
（1）求A、B两种型号的汽车每辆进价分别为多少万元？
（2）若该公司计划正好用180万元购进以上两种型号的新能源汽车（两种型号的汽车均购买），请你帮助该公司设计购买方案；
（3）若该汽车销售公司销售1辆A型汽车可获利8000元，销售1辆B型汽车可获利6000元，在（2）中的购买方案中，假如这些新能源汽车全部售出，哪种方案获利最大？最大利润是多少元？




八年级上学期第一次线上教学反馈答案
一、选择题
1-5：CDADA 6-10:CCDDB
二、填空题
11. ±2
12.
13.
14. cm
15. 或
16. 解：（1）




（2）∵，
∴，
∵a是的小数部分，
∴，



当时，
原式


17. 【小问1详解】
如图，为所作．
【小问2详解】
的面积．
【小问3详解】
设P点坐标为，
∵的面积等于，
∴，
解得或，
∴P点坐标为或．
18. 【小问1详解】
解：甲班15名学生测试成绩从小到大排列为：
78，83，85，87，89，90，92，93，94，95，97，98，99，100， 100．
处在中间位置的是93，∴；
乙班15名学生测试成绩分别为：81，82，83，85，87，96，87，92，94，95，87，93，95，96，97．
出现次数最多的是87，即众数为87，∴，
故答案为：93，87
【小问2详解】
由题意可知甲班15名学生和乙班15名学生的优秀人数分别为6人和5人，则（人），
答：估计参加防疫知识测试的1200名学生中成绩为优秀的学生共有440人；
【小问3详解】
甲班成绩较好，理由如下：
甲班成绩平均数、中位数、众数均大于乙班，只有方差大于乙班，所以甲班的学生防疫测试的整体成绩较好．
19. 【小问1详解】
∵的长度是男孩未拽之前的绳子长，的长度是男孩拽之后的绳子长，绳长始终保持不变，
∴，
故答案为：=；
【小问2详解】
连接，则点A、B、F三点共线，

在中，（米），
∵（米），
∴在中，（米），
∵，
∴（米），
∴男孩需向右移动的距离为米．
20. 【小问1详解】
解：设种型号的汽车每辆进价为万元，种型号的汽车每辆进价为万元，
由题意可得，解得，
答：、两种型号的汽车每辆进价分别为25万元、10万元；
【小问2详解】
解：设购买型号的汽车辆，种型号的汽车辆，
由题意可得且，，
解得或或，
该公司共有三种购买方案，
方案一：购买2辆型汽车，购买13辆型汽车；
方案二：购买4辆型汽车，购买8辆型汽车；
方案三：购买6辆型汽车，购买3辆型汽车；
【小问3详解】
解：当，时，获得的利润为：（元），
当，时，获得的利润为：（元），
当，时，获得的利润为：（元），
由上可得，最大利润为94000元，
购买2辆型汽车，购买13辆型汽车获利最大，最大值为94000元．