


2023年冀教版数学七年级上册《2.2 点和线》课时练习(含答案)
展开2023年冀教版数学七年级上册
《2.2 点和线》课时练习
A.直线有无数个端点 B.线段有2个端点
C.射线没有端点 D.以上都不对
A.射线是直线的一部分
B.线段是直线的一部分
C.直线的长度大于射线的长度
D.直线是可以无限延伸的,射线也是可以无限延伸的
3.如图所示,关于线段、射线和直线的条数,下列说法正确的是( )

A.五条线段,三条射线
B.一条直线,三条线段
C.三条线段,两条射线,一条直线
D.三条线段,三条射线
4.如图,甲、乙两地之间有多条路可走,那么最短路线的走法序号是( )

A.①﹣④ B.②﹣④ C.③﹣⑤ D.②﹣⑤
5.如图所示,夏颖只用两枚钉子就把一根木条固定在墙上,下列语句能解释这个原理的是( )
![]()
A.木条是直的
B.两点确定一条直线
C.过一点可以画无数条直线
D.一个点不能确定一条直线
6.如图,线段AD上有两点B,C,则图中共有线段( )
![]()
A.三条 B.四条 C.五条 D.六条
7.平面上有四个点,经过其中的两点画直线最少可画a条直线,最多可画b条直线,那么a+b的值为( )
A.4 B.5 C.6 D.7
8.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,…,那么6条直线最多有( )
A.21个交点 B.18个交点 C.15个交点 D.10个交点
9.开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为________.
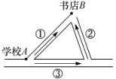
10.如图,从学校A到书店B最近的路线是①号路线,其道理应是____________;
11.直线上的点有____个,射线上的点有____个,线段上的点有____个.
13.如图给出的分别有射线、直线、线段,其中能相交的图形有 个.

14.如图,l1与l2是同一平面内的两条相交直线,它们有一个交点.如果在这个平面内再画第三条直线l3,那么这3条直线最多可有 个交点;如果在这个平面内再画第4条直线l4,那么这4条直线最多可有 个交点.由此,我们可以猜想:在同一平面内,n(n为大于1的整数)条直线最多可有 个交点.(用含n的式子表示)
![]()
15.如图,平面上有四个点P、A、B、C,根据下列语句画图.
(1)画射线PA、PB;
(2)连接AB,交射线PC于点D;
(3)连接AC并延长AC交PB于点E;
(4)取一点F,使F既在射线PA上又在射线BC上.

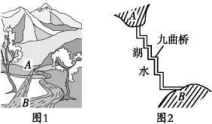
16.(1)如图1所示,把原来弯曲的河道改直,A,B两地间的河道长度有什么变化?
(2)如图2,公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?与修一座直的桥相比,这样做是否增加了游人在桥上行走的路程?说出上述问题中的道理.
17.3个篮球队进行单循环比赛,总的比赛场次是多少?4个球队呢?5个球队呢?
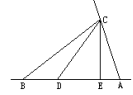
18.如图所示,如果直线l上依次有3个点A,B,C,解答下列问题.
![]()
(1)在直线l上共有多少条射线?多少条线段?
(2)在直线l上增加一个点,共增加了多少条射线?多少条线段?
(3)如果在直线l上增加到n个点,那么共有多少条射线?多少条线段?
19.如图,平面内有六条有公共端点的射线OA,OB,OC,OD,OE,OF,从射线OA开始,
按逆时针方向依次在各条射线上写上数字1,2,3,4,5,6,7,….

(1)数20在射线________上;
(2)请写出六条射线上数字的排列规律;
(3)数2023在哪条射线上?

(2)由于“两点之间,线段最短”,这样做增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光,起到“休闲”的作用.
17.解:用直线上的点代表球队,进行单循环比赛可用线段来表示.
3个球队共比赛用线段AB,BC,AC表示,共有3场;
![]()
4个球队比赛用线段AB,AC,AD,BC,BD,CD表示,共有6场;
![]()
5个球队比赛用线段AB,AC,AD,AE,BC,BD,BE,CD,CE,DE表示,共有10场.
![]()
(2)在直线l上增加一个点,共增加了2条射线,3条线段.
(3)如果在直线l上增加n个点,则共有2n条射线,n(n﹣1)条线段.
19.解:(1)∵20÷6=3……2,∴数20在射线OB上.
(2)规律如下:设n为正整数,则数6n-5在射线OA上;数6n-4在射线OB上;
数6n-3在射线OC上;数6n-2在射线OD上;数6n-1在射线OE上;数6n在射线OF上.
(3)∵2023÷6=337……1,∴数2023在射线OA上.









